【微分方程式】例題で学ぶ:ベルヌーイ型の解法
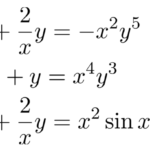
以下のベルヌーイ型と呼ばれる微分方程式(Bernoulli differential equation)の解法を説明する。 特徴は、左辺は線形型に見えるが右辺に が含まれることである。 こ …
もっと読む 【微分方程式】例題で学ぶ:ベルヌーイ型の解法バター猫のパラドックス
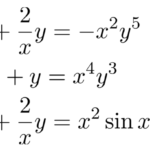
以下のベルヌーイ型と呼ばれる微分方程式(Bernoulli differential equation)の解法を説明する。 特徴は、左辺は線形型に見えるが右辺に が含まれることである。 こ …
もっと読む 【微分方程式】例題で学ぶ:ベルヌーイ型の解法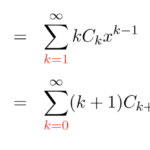
微分方程式を級数解によって解くとは、微分方程式の解の形を などと置いてしまって展開係数 を求める問題に替えて解くことである。例題を見ていこう。 例題 以下の微分方程式を級数を用いて解け。 & …
もっと読む 【微分方程式】例題で学ぶ:級数解による解法(整級数)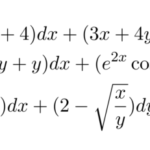
全微分型の微分方程式を解く。全微分型とは の形をしている。これは が分かれば簡単に解ける。 つまり、一般解は である。問題は「いかにして を求めるか」である。例題 …
もっと読む 【微分方程式】例題で学ぶ:全微分型(問題の見分け方/解法)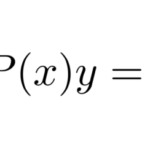
ここでの目的は、線形型の微分方程式 の解き方を習得し、例題を解けるようになることである。このタイプを解くには以下のコツだけ覚えていれば、後に示すような難しい一般解は不要になる。 ポイント 「 …
もっと読む 【微分方程式】公式を覚えず解く「1次線形型」の解法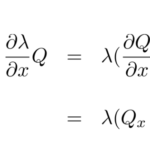
積分因子とは、与えられた微分方程式にかけて完全微分型の微分方程式を作るための因子である。 簡単に言えば、積分因子 を見つけることができれば微分方程式は完全微分型の微分方程式に帰着する。 ここでは、どのような仕組みで積 …
もっと読む 【微分方程式】積分因子の意味と完全微分型(例題で学ぶ)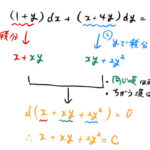
が完全微分型のときは のように変形できる。 したがって、(*)から(*)’を直接求めることができれば簡単に解くことができる。 すなわち、全微分される前の …
もっと読む 【微分方程式】ずるい完全微分型の解法(+例題15問)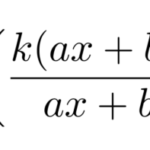
前回の続きから、同次型に似た例題を解いていこうと思う。 ここでは以下のタイプの微分方程式を「変数分離型」に帰着させることを目指す。 右辺の分子・分母をそれぞれ直線と見たとき、平行になる場合で …
もっと読む 【微分方程式】「同次型」に似た問題その(2)/u=ax+by+cと変換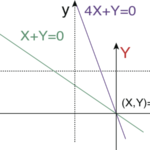
ここでは以下のような同次型に似た問題を扱う。 変数変換により同次型に帰着することがわかる。(同次型がわからない・解けない方は先に「同次型の解法」で解法を習得したほうがよいだろう。) 以下の …
もっと読む 【微分方程式】「同次型」に似た例題その(1)/平行移動による変数変換
時間 世界と 世界の往来。変換表とその証明をまとめる。デルタ関数については別に証明するためここには載せなかった。その他の証明は以下の定義でひたすら計算するが、三角関数を含むものはちょっとしたコツがある。 参考:【はじめに …
もっと読む 【まとめ】ラプラス変換表と証明
ユークリッド互除法をまとめよう。何をやってるかのイメージを知ってもらうため、絵を使ってわかりやすく説明していく。 1. 何のために使うの? ユークリッド互除法の使い道は 2つの数の最大公約数を求められる 分母と分子の …
もっと読む 【絵で見てわかる】ユークリッド互除法 の仕組みと解き方