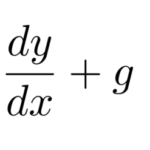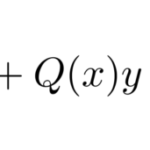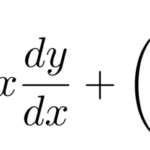積分因子とは、与えられた微分方程式にかけて完全微分型の微分方程式を作るための因子である。 簡単に言えば、積分因子 ![]() を見つけることができれば微分方程式は完全微分型の微分方程式に帰着する。
を見つけることができれば微分方程式は完全微分型の微分方程式に帰着する。
ここでは、どのような仕組みで積分因子を求めるか考えよう。 例題を用意したので解いてみてほしい。 以下の例題はすべて変数分離型でも解くことができる。
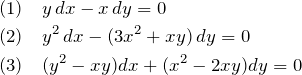
目次
1. 積分因子の求め方と完全微分型の微分方程式
完全微分型について復習し、積分因子の役割を学ぶ。
完全微分型であるための必要十分条件
![]()
の形の微分方程式が完全微分型であるための必要十分条件は
![]()
である。完全微分型の微分方程式であれば
![]()
の形に変形できる。この式は簡単に解ける。
![]()
が完全微分型の微分方程式の解になる。
積分因子の意味
(*)が完全微分型でない場合は上の条件(1)は満たさない。 このとき(*)の両辺にある関数 ![]() をかけて
をかけて
![]()
とする。(*)’が完全微分型の微分方程式となる場合の ![]() を積分因子と呼ぶ。
つまり
を積分因子と呼ぶ。
つまり
積分因子 ![]() によって完全微分型でない式は完全微分型となる
によって完全微分型でない式は完全微分型となる
積分因子の求め方:3パターン
積分因子 ![]() の求め方を説明する。 まず(*)’が完全微分型であるための必要十分条件は
の求め方を説明する。 まず(*)’が完全微分型であるための必要十分条件は
![]()
である。
したがって、
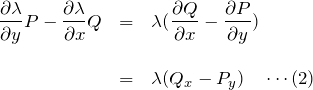
となる ![]() を見つければ良い。
よく使う
を見つければ良い。
よく使う ![]() の形は3パターンある。
の形は3パターンある。
 :
: 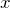 のみの関数
のみの関数 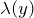 :
: 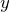 のみの関数
のみの関数 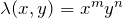 :
: 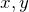 のべきの形
のべきの形
パターン1:
![]() のとき、
のとき、![]() を
を ![]() で偏微分するとゼロ
で偏微分するとゼロ
![]()
である。そうすると式(2)は
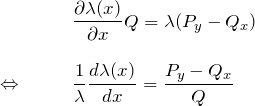
となる。左辺は ![]() のみの関数。 したがって、右辺が
のみの関数。 したがって、右辺が ![]() を含む関数だと矛盾する。 この場合はパターン1の積分因子の形ではない。すなわち、
を含む関数だと矛盾する。 この場合はパターン1の積分因子の形ではない。すなわち、![]() の形である。
の形である。
したがって、パターン1のように積分因数が ![]() のみで表される
のみで表される ![]() のは、
のは、![]() が
が ![]() のみ関数の場合のとき。つまり、
のみ関数の場合のとき。つまり、![]() が
が ![]() の関数であるならば、
の関数であるならば、![]() は
は ![]() のみの関数で、以下のように積分因数を求めることができる。
のみの関数で、以下のように積分因数を求めることができる。
積分因数の求め方(パターン1):
![]()
の右辺は ![]() のみの関数である。したがって、この微分方程式は変数分離型である。
のみの関数である。したがって、この微分方程式は変数分離型である。
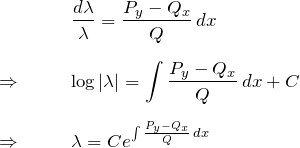
したがって、最も簡単な ![]() をとって
をとって
![]()
が求める積分因数である。
パターン2:
パターン1と同様に考えればよい。
![]()
である。したがって、![]() が
が ![]() の関数であるならば、
の関数であるならば、![]() は
は ![]() のみの関数で、変数分離型を解くことで積分因数を求めることができる。
のみの関数で、変数分離型を解くことで積分因数を求めることができる。
パターン2の積分因数:
![]()
パターン3:
よくある積分因子の形として ![]() とおく形がある。 この形を
とおく形がある。 この形を ![]() それぞれで偏微分すると
それぞれで偏微分すると
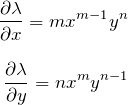
これを (2) へ代入して
![]()
を得る。
具体的な形を考えてみる。
例題(2)について ![]() は
は
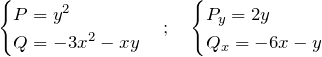
である。したがって、式(3)は
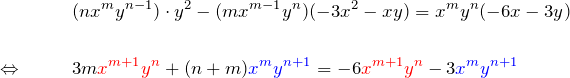
となる。係数を比較して ![]() を得る。 したがって積分因子
を得る。 したがって積分因子 ![]() が求められる。
が求められる。
同次型の微分方程式であれば、積分因子 ![]() を用いることで完全微分型の微分方程式に帰着することができる。いろいろな同次型の問題に対してやってみてほしい。
を用いることで完全微分型の微分方程式に帰着することができる。いろいろな同次型の問題に対してやってみてほしい。
2. 例題の解答
以下の解答で ![]() などは定数を表す。 解答は以下の流れである。大枠をつかんでほしい。
などは定数を表す。 解答は以下の流れである。大枠をつかんでほしい。
- 与えられた式を完全微分型にするために積分因子を求める
- 完全微分型の微分方程式を解く
例題(1)の解答
![]()
まず、与えられた式が完全微分型ではないことを調べよう。
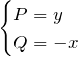
とすると
![]()
であるため完全微分型ではない。
完全微分型ではない(*)に対して、積分因子 ![]() をかけて
をかけて
![]()
このとき、
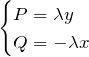
(*)’が完全微分型になるためには
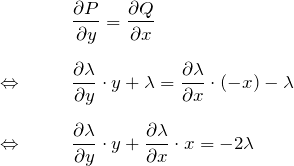
例えば、![]() が
が ![]() のみの関数であれば、
のみの関数であれば、
![]()
より、上の式は
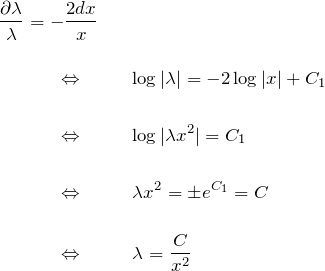
したがって、(*)に積分因子 ![]() をかけて
をかけて
![]()
これは完全微分型である(そうなるように ![]() を決定した)。
を決定した)。
この完全微分型の微分方程式は
![]()
と変形できる。よって
![]()
* ここでは ![]() と、
と、![]() のみの関数で考えてきたが、
のみの関数で考えてきたが、![]() のみの関数でも同様に解ける。
のみの関数でも同様に解ける。
** さらに、![]() の形とおいて解くと、
の形とおいて解くと、![]() であれば積分因子は何でも良いことがわかる。例えば、
であれば積分因子は何でも良いことがわかる。例えば、![]() としても、(*)” は完全微分型になることが確認できるだろう。
としても、(*)” は完全微分型になることが確認できるだろう。
例題(2)の解答
![]()
この微分方程式は
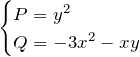
に対して
![]()
である。したがって、(*)は完全微分型ではない。
(*)の両辺に積分因子 ![]() をかけて
をかけて
![]()
が完全微分型になるように ![]() を決定する。
(*)’が完全微分型になるための条件は
を決定する。
(*)’が完全微分型になるための条件は
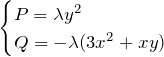
に対して
![]()
が成り立つことである。
したがって、
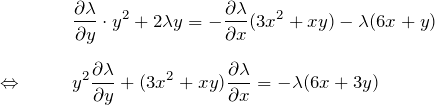
積分因子の形を ![]() とおく:
とおく:
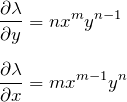
よって
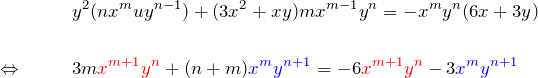
したがって、
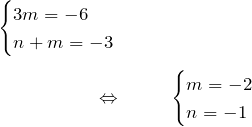
したがって、積分因子は ![]() である。
これを(*)にかけて、
である。
これを(*)にかけて、
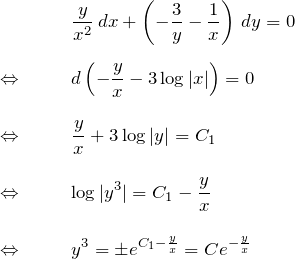
したがって、
![]()
例題(3)の解答
![]()
これも完全微分型ではない。
両辺に![]() をかけて
をかけて
![]()
これが完全微分型の微分方程式になるためには
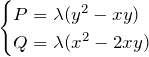
に対して
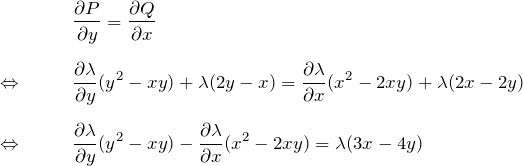
である。
積分因子の形を ![]() とおく:
とおく:
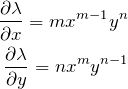
より、
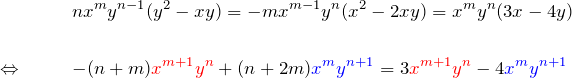
である。したがって、
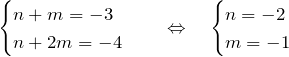
よって、積分因子は ![]() である。
これより、もとの微分方程式 (*) は
である。
これより、もとの微分方程式 (*) は
![]()
となる。これは完全微分型の微分方程式であり、
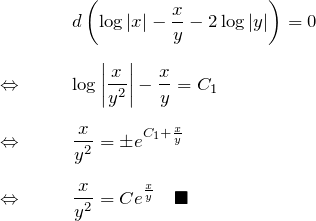
3. まとめ
ここで扱った例題についてはすべて同次型の微分方程式である。 したがって同次型の解法によって解くこともできる。 同次型の微分方程式については、![]() の積分因子を導入することで完全微分型の微分方程式に変形することができる。
の積分因子を導入することで完全微分型の微分方程式に変形することができる。