【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型
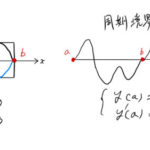
ステュルム-リウヴィル(Sturm-Liouville)型微分方程式 について見ていく。２階微分方程式であるので、解には２つの積分定数が現れる。 この微分方程式を解いて一般解を求めるのではな …
もっと読む 【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型カテゴリー: 数学
【微分方程式】ダランベール型（ラグランジュ型）の解法
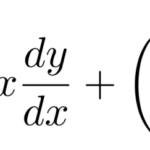
ダランベール型（ラグランジュ型）の微分方程式は以下の形をしている。 のときは、クレローの微分方程式である。 ここでは の一般的なラグランジュの微分方程式を見ていこう。 例題 次の微分方程式を …
もっと読む 【微分方程式】ダランベール型（ラグランジュ型）の解法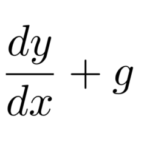
スポンサーリンク
【微分方程式】例題で学ぶ：クレロー型／一般解・特異解／曲線群・包絡線
クレローの微分方程式は の形をしている。 ここではその解き方をまとめて、以下の例題を解けるようにする。包絡線と関係するので、そのことも簡単にまとめる。 よくわからないけど今すぐ解きたいという …
もっと読む 【微分方程式】例題で学ぶ：クレロー型／一般解・特異解／曲線群・包絡線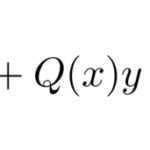【微分方程式】例題で学ぶ：リカッチ(リカティ)型の解法
リカッチ（リカティ、Riccati）の微分方程式は の形をしている。一般的には解けないが、 １つの特解 がわかっているときは とおくことでベルヌーイの微分方程式に帰着して解ける。ベルヌーイ型 …
もっと読む 【微分方程式】例題で学ぶ：リカッチ(リカティ)型の解法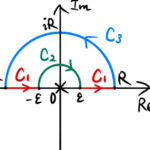【複素積分】sinx/xの実積分（ディリクレ積分）
以下のディリクレ積分と呼ばれる実積分を複素関数を用いた複素積分で解く。 ディリクレ(Dirichlet)積分 1. 複素積分の積分経路 誰か偉い人が考えた積分経路によって解く。 最終的には …
もっと読む 【複素積分】sinx/xの実積分（ディリクレ積分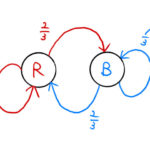）【マルコフ過程】例題2×2の確率遷移行列（行列の対角化・n乗）
マルコフ過程は次の状態が現在の状態のみによって確率的に決まる過程である。ここでは簡単な２状態の間を遷移する例題でマルコフ過程を学ぶの問題というよりは行列の対角化・乗の学習になる。 例題 との２状態について、下の図のよう …
もっと読む 【マルコフ過程】例題2×2の確率遷移行列（行列の対角化・n乗）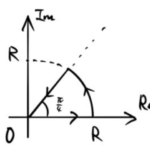
スポンサーリンク
【複素積分】sin(x^2)、cos(x^2)の実積分（フレネル積分）
実積分でそのまま解くことが難しい場合は、複素積分を利用して解くことがある。基本的には、元の実積分が計算できるような積分経路を考えて複素積分していく。今回求めたいのは下の実積分。sinのほうも一緒に求められる。 例題 複 …
もっと読む 【複素積分】sin(x^2)、cos(x^2)の実積分（フレネル積分）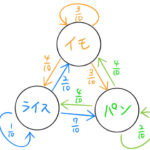
【マルコフ連鎖】3×3遷移確率行列の計算例（卑近な例）
現在の状態が過去の状態によって確率的に決定されるというマルコフ過程（マルコフ連鎖）を説明するために簡単な例を用意した。昨日の朝食によって、今日の朝食が確率的に決まるような話である。見ていこう。 例題 毎日朝食には「ライ …
もっと読む 【マルコフ連鎖】3×3遷移確率行列の計算例（卑近な例）