実積分でそのまま解くことが難しい場合は、複素積分を利用して解くことがある。基本的には、元の実積分が計算できるような積分経路を考えて複素積分していく。今回求めたいのは下の実積分。sinのほうも一緒に求められる。
複素積分を利用して、次の実積分を求めよ。
![]()
目次
1. 複素積分を用いる
ステップバイステップで求める。先人の知恵から、![]() に関する複素積分を、8分の1円を積分経路として行えばよい。
に関する複素積分を、8分の1円を積分経路として行えばよい。
1.1 f(z)をu(x,y)とv(x,y)で表す
後々のために最初に式変形しておく。![]() として複素関数
として複素関数 ![]() は 実関数
は 実関数 ![]() と
と ![]() を用いて
を用いて ![]() と表すことができる。
と表すことができる。
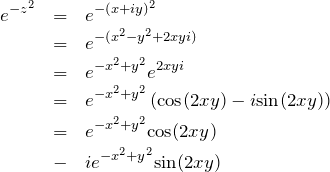
より、
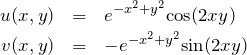
となる。
1.2 積分経路
空から降ってきたかのように次の積分経路を使う。
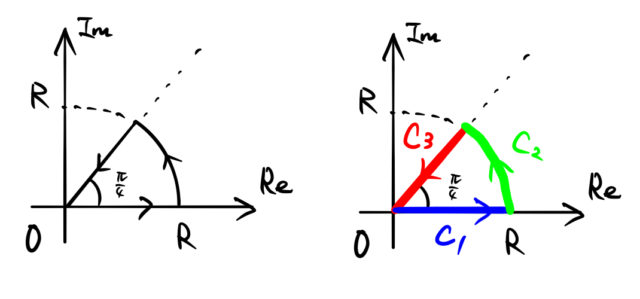
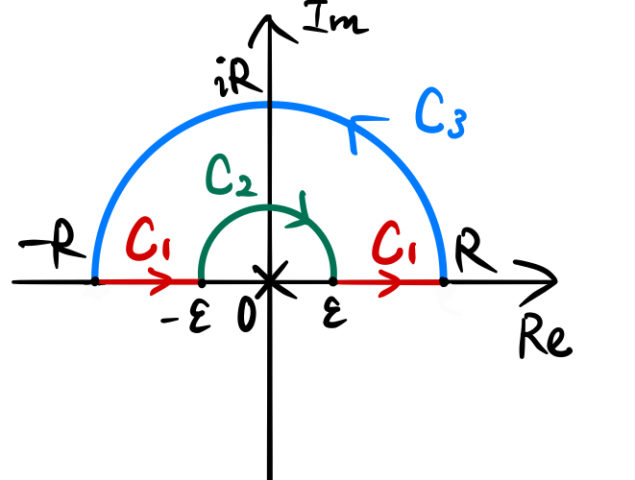
半径 ![]() の8分の1円を積分経路とする。この積分経路は3つに分けられ、積分経路
の8分の1円を積分経路とする。この積分経路は3つに分けられ、積分経路 ![]() は次のように表すことができる。
は次のように表すことができる。
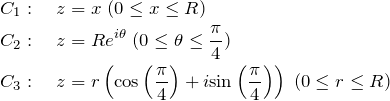
被積分関数は ![]() をとるとうまくいく。
をとるとうまくいく。
![]()
1.1の結果から ![]() は考えている積分経路内に特異点を持たない。これは、
は考えている積分経路内に特異点を持たない。これは、![]() を1.1の
を1.1の ![]() で表した時に
で表した時に![]() が以下の2条件を満たすためである(
が以下の2条件を満たすためである(![]() の正則性の必要十分条件)。
の正則性の必要十分条件)。
- 全微分可能
- コーシー・リーマンの関係式を満たす
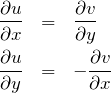
したがって、経路積分内に特異点がないため、コーシーの積分定理より「左辺の周回積分は0」である。あとは右辺の3つの積分経路がどうなるかそれぞれ見ていく。
2. それぞれの複素積分
2.1 C1上の複素積分
![]() 上では
上では ![]() である。したがって、
である。したがって、![]() の極限で、
の極限で、
![]()
右辺の実積分を求める。そのためには右辺の積分を極座標で表して、積分の2乗の値を計算するのがよい。
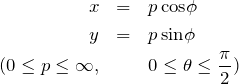
と極座標を用いて、![]() を利用する。また、この極座標変換におけるヤコビアンは
を利用する。また、この極座標変換におけるヤコビアンは ![]() であるため、
であるため、![]() である。
である。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left(\int_{0}^{\infty} e^{-x^2} \,dx\right)^2 &=&\left(\int_{0}^{\infty} e^{-x^2} \,dx\right) \left(\int_{0}^{\infty} e^{-y^2} \,dx\right)\\ \\ &=&\int_0^{\infty}\int_0^{\infty} e^{-(x^2+y^2)} \, dx \, dy \\ \\ &=&\int_{0}^{\frac{\pi}{2}} \int_{0}^{\infty} e^{-p^2} \cdot p\,dr\,d\theta \\ \\ &=&\int_{0}^{\frac{\pi}{2}} \,d\theta \int_{0}^{\infty} pe^{-p^2}\,dr\\ \\ &=&\frac{\pi}{2} \left[ -\frac{1}{2}\,e^{-p^2} \right]_{0}^{\infty}\\ \\ &=&\frac{\pi}{4} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6b17e85c2ef828d9687c58651cc1aaad_l3.png)
求めたい積分の2乗の値がわかった。これより、![]() に注意して正符号のものをとったものが答えになる。
に注意して正符号のものをとったものが答えになる。
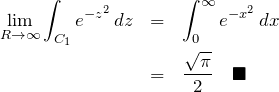
2.2 C2上の複素積分
![]()
結果から言うとこの積分は0に収束する。それを証明する。
【証明】 ![]() 上では
上では ![]() である。これにより積分変数を
である。これにより積分変数を ![]() から
から ![]() に変換する。
に変換する。
![]()
より、
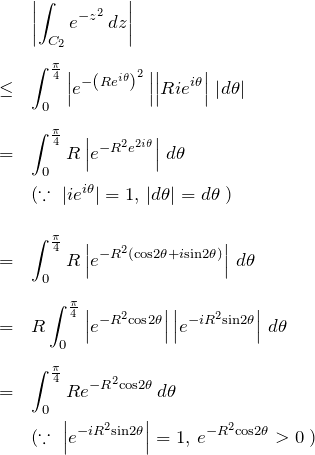
ここで、
![]()
より、
![]()
となる。したがって、
![]()
2.3 C3上の複素積分
![]() より、
より、
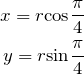
として、1.1の結果を用いる。まず、
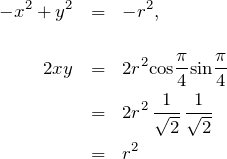
である。したがって、1.1の結果を用いて ![]() を
を ![]() の形で表すと、
の形で表すと、
![]()
![]() より
より ![]() の積分範囲は
の積分範囲は ![]() から
から ![]() であることに注意して、
であることに注意して、
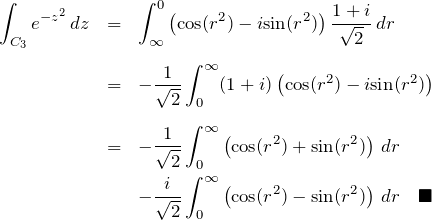
のように実部と虚部に分けることができる。
3. すべての積分の和=0
1.2の結果より、3つの経路の複素積分の和は0になる。
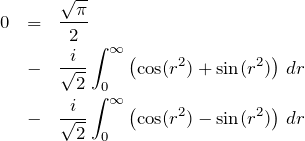
虚部と実部に分けて、
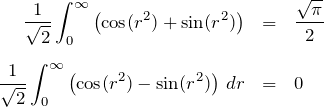
下の式より、
![]()
である。これを上の式に代入して、
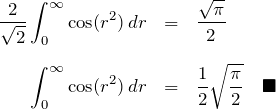
となる。これが有名なフレネル積分である。
![]()
4. まとめ
積分経路をうまくとることでフレネル積分を求められた。経路の取り方は先人たちの知恵を生かすのが良い。ここで導いたフレネル積分は、光学の分野で現れる重要な式である。