カテゴリー: フーリエ変換／ラプラス変換

　フーリエ変換を解説していきましょう。ここではフーリエ変換がどんなものか知ってもらうため、数式を使わないことにした。したがって、フーリエ変換の定義すらしない。 1. フーリエ変換のイメージ（基本編） 1.1 わかりやすい …

　ラプラス変換は微分方程式を解くための道具でしかない。ここでは、面倒な積分計算は書かずにイメージだけ伝えたい。ラプラス変換の応用の要点は微分方程式・積分方程式を簡単に解くために遠回りするということである。解きたい方 …

時間世界と世界の往来。変換表とその証明をまとめる。デルタ関数については別に証明するためここには載せなかった。その他の証明は以下の定義でひたすら計算するが、三角関数を含むものはちょっとしたコツがある。参考：【はじめに …

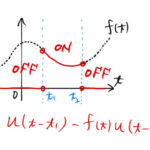
　以下のヘヴィサイドの単位関数は応用上重要である。ここでは単位関数について簡単に説明し、そのラプラス変換について学ぶ。ラプラス逆変換の例題　次のに関する関数をラプラス逆変換してを求めよ。また、を図示せよ。 …

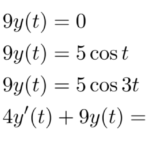
　前回はラプラス変換を用いた斉次線形微分方程式を扱った。ここでは例題を通して非斉次の線形微分方程式を解いていく。例題(1)は斉次、(2)(3)(4)は非斉次の微分方程式である。例題次のに関する微分方程式を解け。 …

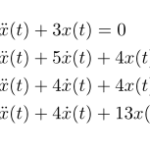
　例題を使って微分方程式の初期値問題をラプラス変換で解く。初期値が与えられている微分方程式はラプラス変換によってをかんたんに解くことができる。ここでは下の例題のような単純な斉次線形微分方程式を解いていく（非斉次微分方 …

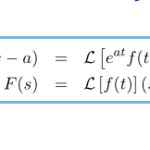
　例題を使ってラプラス逆変換でよく使う「移動」について説明する。ここではなどのラプラス逆変換については理解しているものとして進めていく。移動とは以下のような逆変換のことである。参考：ラプラス変換表と証明まとめ s移 …

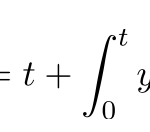
基本的な流れ：に関する積分方程式をラプラス変換の形に変形（部分分数分解など）ラプラス逆変換でを求める例題で定義された実関数を考えて、以下の積分方程式をラプララス変換を用いて解け。 …

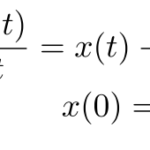
簡単な以下の微分方程式をラプラス変換を用いて解く。【解答】をラプラス変換したを定義する。与えられた微分方程式の両辺をラプラス変換する。世界世界。 &nb …

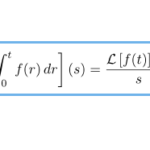
積分のラプラス変換これを導出する。これを利用した下のラプラス逆変換の例題も解説する。ラプラス逆変換の例題次の関数をラプラス逆変換せよ。 1. 積分のラプラス変 …