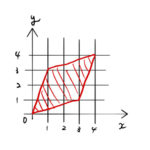
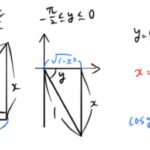
【重積分】面積のイメージで学ぶ「ヤコビアン」の意味 ここではヤコビアンのイメージを伝えるため、 2変数関数の重積分（面積）を例にとる。 平面→ 平面の変数変換に … もっと読む 【重積分】面積のイメージで学ぶ「ヤコビアン」の意味
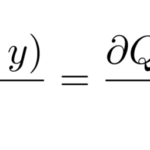
【全微分】関数がf(x,y)の全微分であるための必要十分条件（証明） ここでは、全微分の形がどうか調べる方法を学ぶ。 応用として、完全微分型の微分方程式を解く上で非常に重要である … もっと読む 【全微分】関数がf(x,y)の全微分であるための必要十分条件（証明）
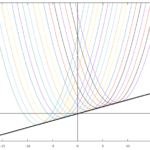
【多変数関数】よくわかる包絡線／包絡線の求め方 包絡線の求め方を例題を通して習得する。求め方は媒介変数を消去すればいいのだが、なぜだろうか。ここでは、包絡線 … もっと読む 【多変数関数】よくわかる包絡線／包絡線の求め方
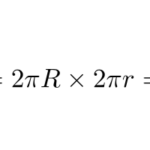
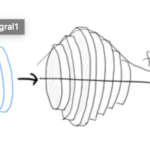
【積分】パップス=ギュルダンの定理でトーラスの体積・表面積 高校数学で使うのは禁忌とされている(?)パップスギュルダンの定理を用いて、トーラス(穴1個のドーナツ)の体積 … もっと読む 【積分】パップス=ギュルダンの定理でトーラスの体積・表面積
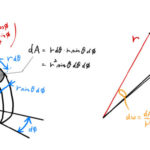
【積分】立体角とは／立体角ω 積分を平面角θ、φに直す 立体角 の解説をおこないます。微小立体角と微小平面角の関係は以下。 微小立体角から微小平面角 … もっと読む 【積分】立体角とは／立体角ω 積分を平面角θ、φに直す
【微分】ラプラシアンΔの極座標表示を導く計算 シュレディンガー方程式のハミルトニアンに含まれるラプラシアンΔを極座標に変換するときの計算をおこなう。ラプ … もっと読む 【微分】ラプラシアンΔの極座標表示を導く計算
