シュレディンガー方程式のハミルトニアンに含まれるラプラシアンΔを極座標に変換するときの計算をおこなう。ラプラシアンに2階微分が入っているため、![]() の変換は手間がかかることを知ってもらいたい。よく見る Δ の極座標表示は以下の通り。
の変換は手間がかかることを知ってもらいたい。よく見る Δ の極座標表示は以下の通り。
ラプラシアンΔの極座標表示
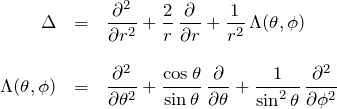
目次
1. 1階微分の極座標表示
1階微分の極座標表示の導出過程は以下を参考にすると良い。
ここでは1階微分については最終的な結果だけ示しておく。
1階微分の極座標表示
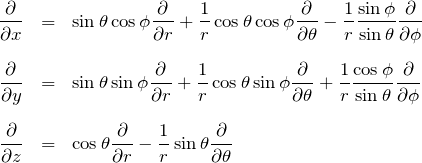
2. ラプラシアンΔの極座標表示
ラプラシアンの ![]() 表示は、
表示は、
![]()
であり、2階偏微分を含むため変換は厄介である。導出は、
- 1階偏微分の変換(項目1で示した)
- 2階偏微分の変換
の手順で計算する。
2.1 ∂^2/∂x^2
![]() を2回使う。
を2回使う。
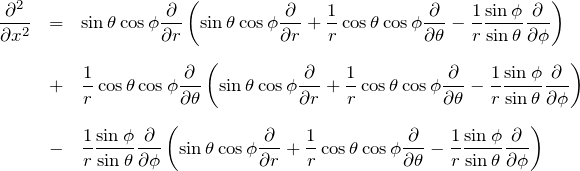
1行目
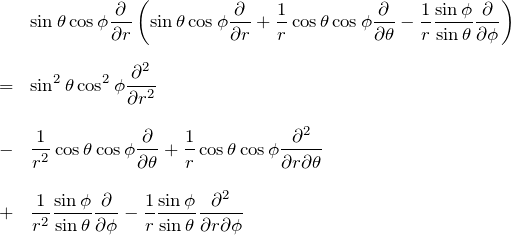
間違えやすいポイント
間違えがちなポイント
![]()
これは適当な関数 ![]() を用意すればわかると思う。
を用意すればわかると思う。
![]()
何が ![]() の関数になっているところがはっきりしていれば間違えにくい。
の関数になっているところがはっきりしていれば間違えにくい。
2行目
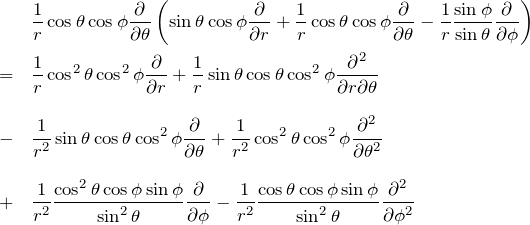
3行目
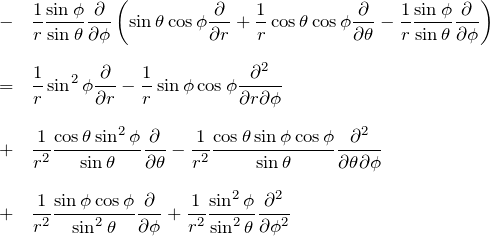
2.2 ∂^2/∂y^2
同様に計算する。
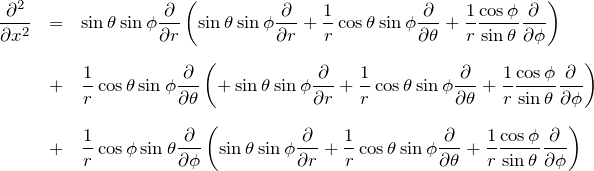
1行目
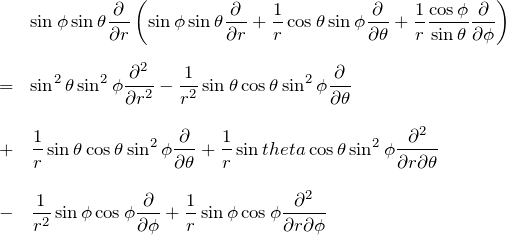
2行目
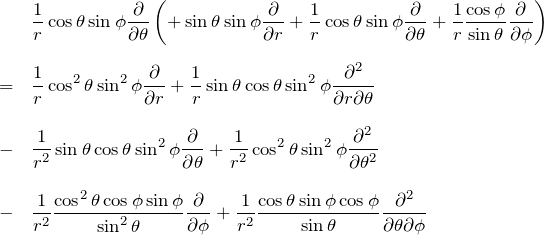
3行目
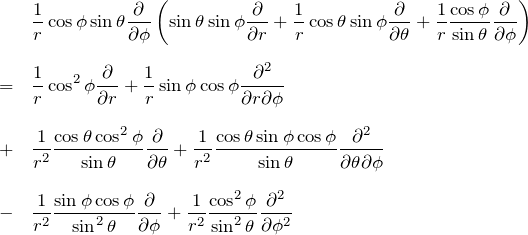
2.3 ∂^2/∂z^2
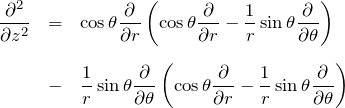
1行目
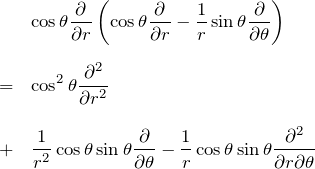
2行目
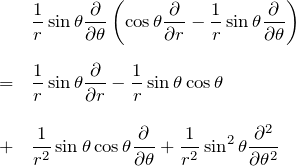
2.4 ∂^2/∂x^2 + ∂^2/∂y^2 + ∂^2/∂z^2
方針:項ごとに係数を計算して、まとめる。
![]() :
:
![]()
![]() :
:
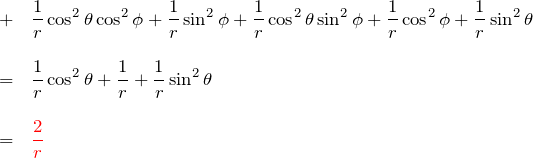
![]() :
:
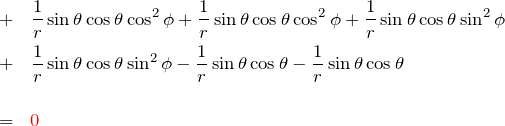
![]() :
:
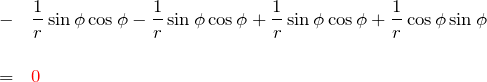
![]() :
:
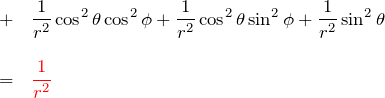
![]() :
:
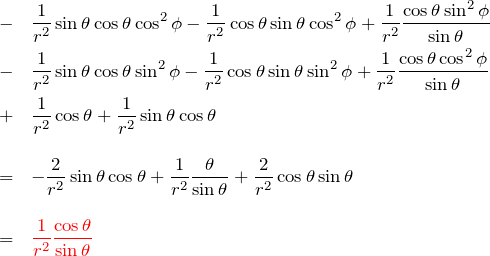
![]() :
:
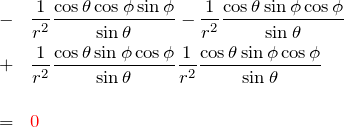
![]() :
:
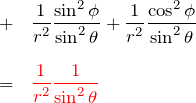
![]() :
:
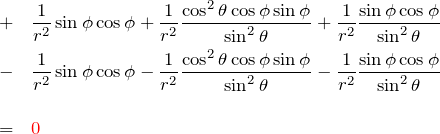
2.5 全部足す
以上をまとめることで、ラプラシアンの極座標表示が求められる。
ラプラシアンΔの極座標表示
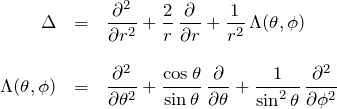
3. まとめ
大変な計算量でした。お疲れ様でした。途中の「間違えやすいポイント」にさえ注意すれば、ラプラシアンの極座標表示は求められます。