ラーゲル多項式(陪多項式)、ルジャンドル多項式(陪多項式)、球面調和関数など、球対称ポテンシャル ![]() をもつ極座標表示のシュレディンガー方程式を解く過程で複雑なものがたくさん出てくる。ここではもう、2.1以降でざっくりとまとめてしまおう。
をもつ極座標表示のシュレディンガー方程式を解く過程で複雑なものがたくさん出てくる。ここではもう、2.1以降でざっくりとまとめてしまおう。
目次
1. 極座標表示のシュレディンガー方程式と変数分離
1.1 極座標表示のシュレディンガー方程式
水素原子のシュレディンガー方程式を解くときなどには角度 ![]() に依存しない球対称ポテンシャル
に依存しない球対称ポテンシャル ![]() を考える。このとき、極座標表示されたシュレディンガー方程式は、
を考える。このとき、極座標表示されたシュレディンガー方程式は、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[ -\frac{\hbar^2}{2m_e}\left( \frac{\partial^2}{\partial r^2}+\frac{2}{r}\frac{\partila}{\partial r}+\frac{1}{r^2}\Lambda(\theta,\phi) \right)+V(r) \right]\Phi(r,\theta,\phi)=E\Phi(r,\theta,\phi) \\ \\ \Lambda(\theta,\phi)=\frac{\partial^2}{\patial \theta^2} +\frac{\cos\theta}{\sin\theta}\frac{\partia}{\partial \theta} +\frac{1}{\sin^2{\theta}}\frac{\partial^2}{\partial \phi^2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-55284c2d2a35c5f08a2465993c5fddd2_l3.png)
で表すことができる。
1.2 変数分離
![]() は
は ![]() に依存しない演算子である。したがって、上の極座標のシュレディンガー方程式の両辺に
に依存しない演算子である。したがって、上の極座標のシュレディンガー方程式の両辺に ![]() をかけると、
をかけると、![]() に関する部分と
に関する部分と ![]() に関する部分に分けることができる。
に関する部分に分けることができる。
したがって、シュレディンガー方程式の解を2つの関数に変数分離する。
![]()
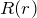 :動径関数、
:動径関数、 のみの関数
のみの関数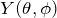 :角度の関数、
:角度の関数、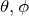 の関数
の関数
のちに、量子数 ![]() によって関数の形が決められる。
によって関数の形が決められる。
1.3 2つの式に分ける
極座標のシュレディンガー方程式に ![]() をかけて、変形しよう。
をかけて、変形しよう。
![]()
左辺と右辺で独立変数の関数であるために、両辺は定数になる。後のために適当な定数を用いて、2つの式に分ける。
右辺:
![]()
左辺:
![]()
ざっくり言うと、
- 上の式→ルジャンドル多項式、球面調和関数
- 下の式→ラーゲル多項式
の話につながる。
2. ざっくりとした説明
2.1 球面調和関数・ルジャンドル多項式
上の角度の関数 ![]() をさらに変数分離して
をさらに変数分離して
![]()
として上の方程式を解く。結果だけまとめる。
![]() :
:
- すぐ求められる。
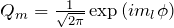
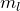 は
は 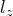 の固有値(磁気量子数)
の固有値(磁気量子数)
![]() :
:
- ルジャンドル多項式になる
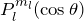 で表される
で表される- 方位量子数
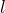 と磁気量子数
と磁気量子数 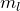 で決まる
で決まる 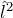 の固有値は
の固有値は 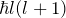
![]() :
:
- 球面調和関数
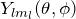 になる
になる - 方位量子数
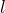 と磁気量子数
と磁気量子数 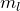 で決まる
で決まる 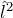 と
と 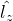 の固有関数
の固有関数- 軌道の形を決めている
【参考】ルジャンドル多項式の導出(ルジャンドルの微分方程式)
【参考】球面調和関数⓪:ルジャンドリアンの固有値問題
【参考】球面調和関数①:シュレディンガー方程式からの導出
2.2 ラーゲル多項式・動径波動関数
![]() に関する方程式から
に関する方程式から ![]() を求める。結果だけを示す。
を求める。結果だけを示す。
![]() :
:
- 動径波動関数
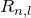 で表される
で表される - 主量子数
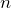 と 方位量子数
と 方位量子数 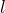 で形が決まる
で形が決まる 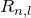 の中にラーゲル陪多項式
の中にラーゲル陪多項式 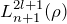 が含まれる
が含まれる
動径波動関数の式だけ載せておく。
![Rendered by QuickLaTeX.com \begin{eqnarray*} R_{n,l}(r)=-\sqrt{\left(\frac{2}{na_0}\right)^3 \frac{(n-l-1)!}{2n[(n+l)!]^3}} \left(\frac{2r}{na_0}\right)^l \exp{\left(- \frac{r}{na_0} \right)} L_{n+1}^{2l+1}\left(\frac{2r}{na_0}\right) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-954151614b465f48aeac4b23845e868a_l3.png)
ここで、![]() はボーア半径である。
はボーア半径である。
3. まとめ
本当は軌道の話につなげて視覚化するのが良いと思うが、ここでは全体像を知れるように大まかにまとめた。
なぜ、こんなにもわかりにくいかと言うと、
- 式が複雑で授業や教科書では省略される
- 3つも4つも関数や多項式が出てきて覚えにくい
ことが原因であろう。その割に波動関数や軌道に関わる非常に重要な話だから落とせないのです。