マルコフ過程は次の状態が現在の状態のみによって確率的に決まる過程である。ここでは簡単な2状態の間を遷移する例題でマルコフ過程を学ぶの問題というよりは行列の対角化・![]() 乗の学習になる。
乗の学習になる。
![]() と
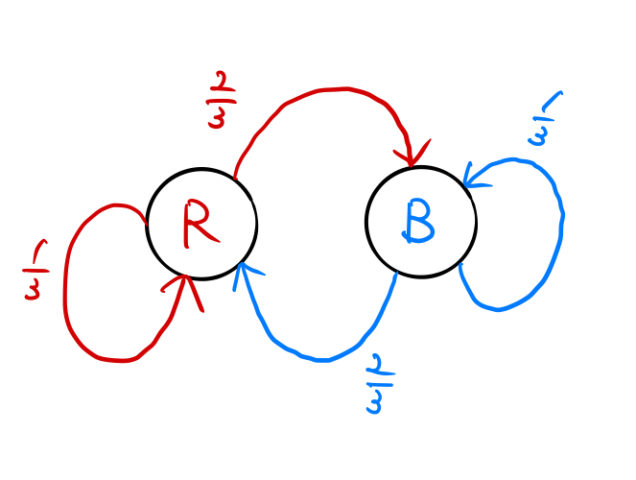
と![]() の2状態について、下の図のように遷移する過程を考える。はじめ、
の2状態について、下の図のように遷移する過程を考える。はじめ、![]() にあったとき以下の確率を求めよ。
にあったとき以下の確率を求めよ。
(1) 1回の遷移で ![]() にいる確率と
にいる確率と ![]() にいる確率
にいる確率
(2) 2回の遷移で ![]() にいる確率
にいる確率
(3) ![]() 回の遷移で
回の遷移で ![]() にいる確率
にいる確率
目次
1. 1回の遷移を表す遷移行列
遷移行列を用いて2状態を記述するのが良い。
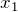 :1回目の遷移で
:1回目の遷移で 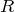 にいる確率
にいる確率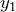 :1回目の遷移で
:1回目の遷移で 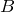 にいる確率
にいる確率- 初期状態は
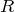 にいる(
にいる( 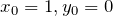 )
)
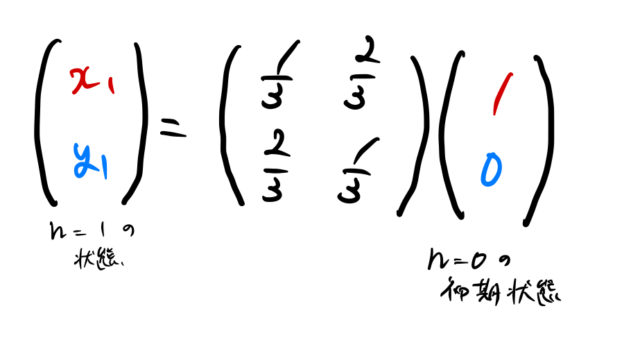
ここで遷移行列を ![]() と置いておく。
と置いておく。
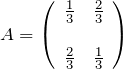
例題(1)の答えは簡単に求められる。
![]()
である。![]()
2. 2回の遷移でどうなるか?
2.1 1回遷移したあとの状態から考える
例題(2)は(1)の答えを用いれば簡単に計算できる。
2回目の遷移は1回目の遷移が終わった状態のみに依存する。つまり、初期状態の情報は1回目の遷移が終わった後の状態に集約されている。
行列を使って(2)を解くと以下のようになる。
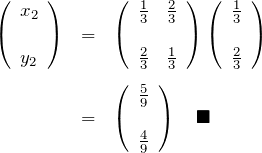
2.2 初期状態からの遷移を追う
1回遷移が終わった状態から考える代わりに、初期状態から遷移確率行列 ![]() を用いて2回の遷移を考える。つまり、下のように、
を用いて2回の遷移を考える。つまり、下のように、![]() を考えれば良い。
を考えれば良い。
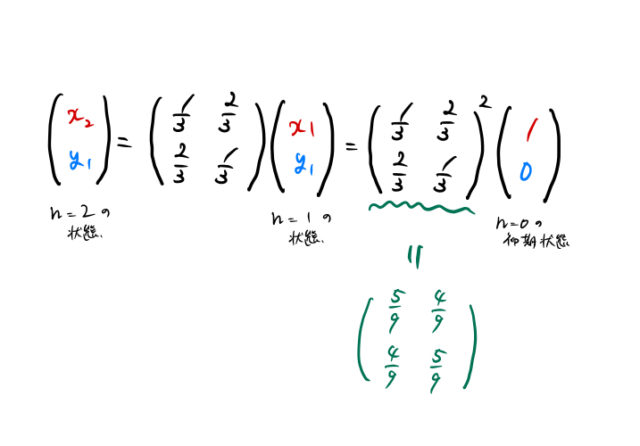
当然1回遷移が終わった状態から求めた 2.1 の結果と同じになる。
3. n回遷移した状態
3.1 遷移行列を使って解く
初期状態から ![]() 回の遷移があるため、遷移行列を
回の遷移があるため、遷移行列を ![]() 乗した(
乗した(![]() )。
)。
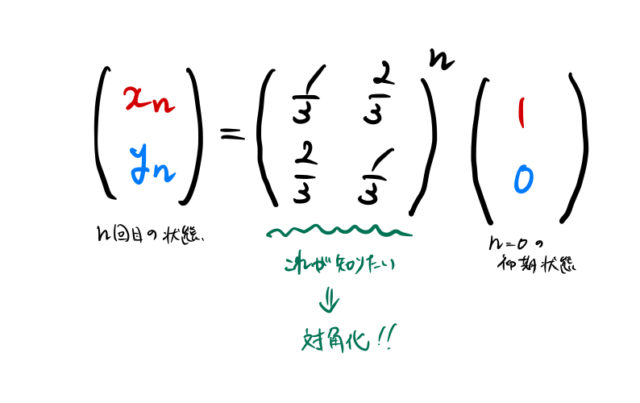
答えの ![]() を求めるためには、
を求めるためには、![]() が知りたい。したがって、
が知りたい。したがって、
- 固有値・固有ベクトルを求める
- 対角化する
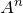 を求める
を求める
ことをすればよい。簡単な行列の対角化の問題である。
3.2 行列のn乗計算
固有値:
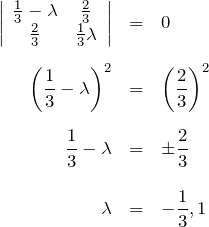
![]() の固有ベクトル:
の固有ベクトル:
![]()
![]() の固有ベクトル:
の固有ベクトル:
![]()
2つの固有ベクトルは規格化しておいた。上の2つの固有ベクトルは以下の性質をもつ。
- 規格化されている
- 互いに直交する
したがって、この2つの固有ベクトルによって作られる行列 ![]() は、
は、
![]()
でユニタリ行列である。ユニタリ行列の逆行列は転置行列で与えられる(この場合は![]() 行列なので別の方法でも簡単に求めることができる)。
行列なので別の方法でも簡単に求めることができる)。
![]()
対角化:
対角化行列を ![]() とする。
とする。
![]()
![]() を求める:
を求める:
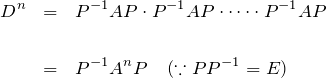
よって、
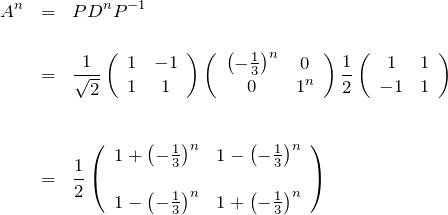
である。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left(\begin{array}{cc} x_n \\ \\ y_n \end{array}\right)&=& \frac{1}{2} \left(\begin{array}{cc} 1+\left(-\frac{1}{3}\right)^n & 1-\left(-\frac{1}{3}\right)^n \\ \\ 1-\left(-\frac{1}{3}\right)^n & 1+\left(-\frac{1}{3}\right)^n \end{array}\right) \left(\begin{array}{cc} 1 \\ \\ 0 \end{array}\right) \\ \\ \\ &=& \left(\begin{array}{cc} \frac{1}{2}\left[1+\left(-\frac{1}{3}\right)^n\right]\\ \\ \frac{1}{2}\left[1-\left(-\frac{1}{3}\right)^n\right] \end{array}\right) \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a6e316001f74282667ff16d8b697cd6b_l3.png)
これが答えである。![]() の値は例題(1)(2)の結果と一致する。
の値は例題(1)(2)の結果と一致する。
3.3 漸化式
![]() と
と ![]() の関係に注目すれば漸化式が作れる。
の関係に注目すれば漸化式が作れる。
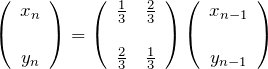
より、
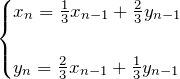
2式を足した式、引いた式をつくる。
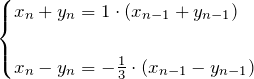
1つ目の式(公比1の等比数列):
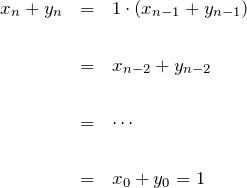
2つ目の式(公比-1/3の等比数列):
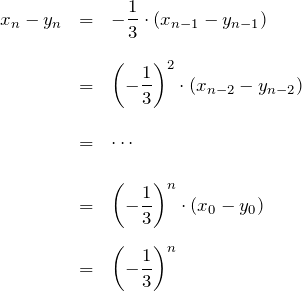
したがって、
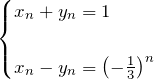
である。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{cases} x_n = \frac{1}{2}\left[1+\left(-\frac{1}{3}\right)^n\right] \\ \\ y_n = \frac{1}{2}\left[1-\left(-\frac{1}{3}\right)^n\right] \end{cases}\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-140d8afbe779e942e056b7891ce546b8_l3.png)
行列を用いた方法と同じ結果を得る。
4. まとめ
遷移確率行列を用いて解いてもらっても良い。漸化式を用いて解いてもらっても良い。漸化式のところでは、明らかに遷移確率行列の固有値、固有関数の形が出ている。これは、
基底 ![]()
![]() 新たな基底
新たな基底 ![]()
としているようにも見える。例えば、
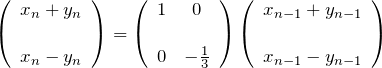
のように書ける。したがって、漸化式で解いた方法も中身は行列の対角化の方法と同じことである。