【マルコフ過程】例題2×2の確率遷移行列(行列の対角化・n乗)
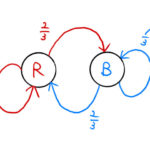
マルコフ過程は次の状態が現在の状態のみによって確率的に決まる過程である。ここでは簡単な2状態の間を遷移する例題でマルコフ過程を学ぶの問題というよりは行列の対角化・乗の学習になる。 例題 との2状態について、下の図のよう …
もっと読む 【マルコフ過程】例題2×2の確率遷移行列(行列の対角化・n乗)バター猫のパラドックス

マルコフ過程は次の状態が現在の状態のみによって確率的に決まる過程である。ここでは簡単な2状態の間を遷移する例題でマルコフ過程を学ぶの問題というよりは行列の対角化・乗の学習になる。 例題 との2状態について、下の図のよう …
もっと読む 【マルコフ過程】例題2×2の確率遷移行列(行列の対角化・n乗)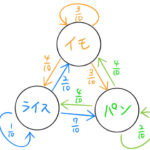
現在の状態が過去の状態によって確率的に決定されるというマルコフ過程(マルコフ連鎖)を説明するために簡単な例を用意した。昨日の朝食によって、今日の朝食が確率的に決まるような話である。見ていこう。 例題 毎日朝食には「ライ …
もっと読む 【マルコフ連鎖】3×3遷移確率行列の計算例(卑近な例)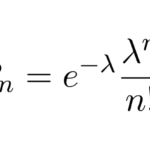
Poisson分布(ポアソン分布)は以下のような確率分布をもつ。 は平均値である。また、Poisson分布の平均値と分散は である。平均も分散も になる。 この …
もっと読む 【確率・統計】Poisson分布の期待値・分散/Poisson分布の導出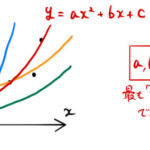
最小二乗法の基本的な説明は以下に記載した。ここでは、2次元データ点に対して二次関数、三次関数のフィッティング式を導く。 二次関数でフィッティング 二次関数の場合は、与えられたデータ点に対して を求めれば良い。下図のよ …
もっと読む 【最小二乗法】二次関数/三次関数でフィッティング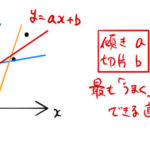
ここではデータ点を 一次関数 を用いて最小二乗法でフィッティングする。二次関数・三次関数でのフィッティング式は こちら 。 下の5つのデータを直線でフィッティングする。 1. 最小二乗法とは? フィッティングの意味 フ …
もっと読む 【最小二乗法】わかりやすく絵で説明/直線フィッティングの計算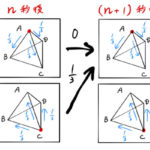
確率漸化式でよくある問題として、正四面体の点の移動を図解する。例題は以下の通り。 例題 四面体ABCDの頂点を移動する点がある 1秒ごとに隣り合う頂点へ1/3の確率で移動する n秒後に点が頂点Aにいる確率を とする は …
もっと読む 【確率漸化式】正四面体の点の移動を図解(高校数学)