全記事一覧 > 数学 > 確率・統計

【分配関数】Zの意味：例を使って確率と期待値を求める。

　分配関数って難しいようで単純なのです。単なる状態和を表しているのですから。結局は、確率の規格化のようなものをイメージすればわかりやすいでしょう。この記事では、分配関数を簡単に説明していきます。

　ここではあまり統計力学の深淵まで掘り下げず、わかりやすくまとめて、計算できるくらいのレベルまで持っていきます。

分配関数

    \begin{eqnarray*}Z(\beta)=\sum_{i}\exp{(-\beta\epsilon_i)}\end{eqnarray*}

　

　

　

1. 分配関数

ポイント

（分配関数）＝（状態和）

　状態和とは何だろう。簡単な確率の問題までさかのぼるとわかりやすい。

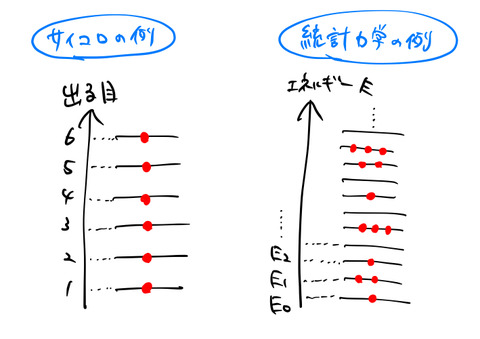
1.1 サイコロの例

　さいころを1回ふる時に出る目は6通りある。このとき、出る目を X とすればそれぞれの確率 P(X_i)=\frac{1}{6}\quad (X\in\{1,2,3,4,5,6\}) となるだろう。この時の状態和を計算しよう。

状態和

状態和（とりうる状態の確率の総和）は以下のように求められる。

    \begin{eqnarray*}\sum_{X\in \Omega }P(X)\end{eqnarray*}

ここで、\Omega はとりうる状態を表す。

　サイコロの例の場合は、\Omega=\{1,2,3,4,5,6\}である。単に、Xが1から6までの値をとるだけの話である。したがって、状態和は、

    \begin{eqnarray*}Z&=&\sum_{X\in\Omega }P(X)\\&=&P(1)+P(2)+P(3)+P(4)+P(5)+P(6)\\&=&6\cdot \frac{1}{6}\\&=&1\end{eqnarray*}

となります。これはすでに規格化 (Z=1) されている状態です。あたりまえです。我々は、確率の総和が1となることを知っているのですから。

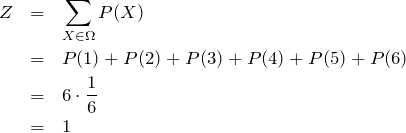
　もし我々がそれぞれの状態を取りうる確率の比（相対的な確率）しかわからない場合はどうなるだろうか。例えば、1から6の目のうち、それぞれの数字が出る確率の比は1:1:1:1:1:1だろう。これを規格化されていない確率 P'(X)=1\quad (X\in\{1,2,3,4,5,6\}) として考える。このとき状態和は、

    \begin{eqnarray*}Z&=&\sum_{X\in \Omega }P'(X)\\&=&P'(1)+P'(2)+P'(3)+P'(4)+P'(5)+P'(6)\\&=&6\cdot 1\\&=&6\end{eqnarray*}

となる。Z\neq1 なのでいまの確率 P'(X)=1 は規格化されていないことがわかる。ということは、規格化した確率が求めたいときは、

    \begin{eqnarray*}\frac{P'(X)}{Z}=\frac{P'}{\sum_{X\in\Omega} P'(X)}\equiv P(X)\end{eqnarray*}


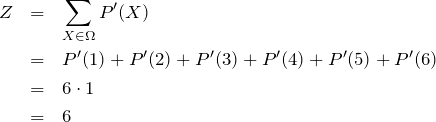
のように分配関数で割るのが良さそうである。いま、Z=6 なのでそれぞれの確率は P(X)=\frac{1}{6} に一致する。

1.2 統計力学の確率と分配関数

　サイコロのように1つの値（出る目）に対して、状態数は1であった。統計力学では、一つの値（エネルギー）に対して状態数が1であるとは限らない。

IMG_20378921E899-1

　図の赤丸は、そのエネルギーを占有している様子を示している。統計力学では、状態数は0, 1, 2, 3, …となりうる（フェルミ粒子なら占有数は0か1）。いま、エネルギーの小さい状態から 状態i=0,1,2,3,... する。図の状態数は、E_0=1,\;E_1=2,\;E_2=1,... である。

　では、それぞれのエネルギーを取りうる確率はいくらであろうか。実はこれらの相対的な確率はボルツマン因子で与えられることが知られている。

ボルツマン因子

 

    \begin{eqnarray*}\exp{(-\beta E_i)}=\exp{(-\frac{E_i}{k_B T})}\end{eqnarray*}

k_B：ボルツマン定数、T：温度、E_i：状態iのエネルギー

　つまり、エネルギーがわかれば相対的な確率（確率の比）がわかるのである。

　いま、相対的な確率しかわからないので、確率の和が1になっていない。すなわち、規格化が必要である。サイコロの例と同様に、エネルギー E_i にある相対確率を P'(E_i)=\exp{(-\beta E_i)} として、分配関数 Zを具体的に書いてみる。

    \begin{eqnarray*}Z&=&\sum_{i\in \Omega }P'(E_i)\\ \\&=&P'(E_1)+P'(E_2)+P'(E_2)+P'(E_2)+P'(E_3)\\&+&P'(E_5)+P'(E_5)+P'(E_5)+P'(E_7)+\cdots\\ \\\end{eqnarray*}

このとき図において、とりうる状態 \Omega は、

    \begin{eqnarray*}\Omega=\{1,\,2,\,2,\,3,\,5,\,5,\,5,\,7,\,\cdots\}\end{eqnarray*}

に注意してほしい。

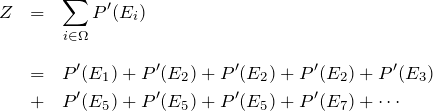
　先に述べたように　この確率の和は1になっているとは限らない(Z\neq 1)。したがって、Z=1 で規格化された絶対確率を知りたいときは、相対確率を Z で割ってやれば良い。相対確率 P' から絶対確率 P にするためには、

    \begin{eqnarray*}P(E_i)&=&\frac{P'(E_i)}{Z}=\frac{P'(E_i))}{\sum_{i\in\Omega} P'(E_i)}\end{eqnarray*}


とすればよい。ここに、 P'(E_i)=\exp{(-\beta E_i)} を代入して、統計力学で重要な確率を得る。

エネルギー E_i の状態 i が現れる確率 {P}(E_i)

    \begin{eqnarray*}{P}(E_i)=\frac{\exp{(-\beta E_i)}}{\sum_{i\in \Omega}\exp{(-\beta E_i)}}\end{eqnarray*}

1.3 統計力学の期待値と分配関数

　もし期待値が知りたいのであれば、サイコロの期待値を求める \sum_{X}XP(X) と同様して求めればよい。つまり、熱平衡状態におけるエネルギーの期待値は、

    \begin{eqnarray*}\sum_{i\in \Omega}E_i P(E_i)&=&\sum_{i\in \Omega}\frac{E_i\exp{(-\beta E_i)}}{\sum_{i\in \Omega}\exp{(-\beta E_i)}}\\ \\&=&\frac{\sum_{i\in \Omega} E_i\exp{(-\beta E_i)}}{\sum_{i\in \Omega}\exp{(-\beta E_i)}}\\ \\&=&-\frac{\partial}{\partial\beta}\left(\ln \left[ \sum_{i\in\Omega }\exp{(-\beta E_i)}\right] \right)\\ \\&=& -\frac{\partial (\ln Z)}{\partial\beta}\end{eqnarray*}

3行目では、対数関数の微分 \frac{\partial}{\partial x}\ln(f(x))=\frac{f'(x)}{f(x)} を利用した。重要な式なのでまとめておく。

熱平衡状態におけるエネルギーの期待値

    \begin{eqnarray*}\sum_{i\in \Omega}E_i P(E_i)=-\frac{\partial (\ln Z)}{\partial\beta}\end{eqnarray*}

　ここで、 \beta=\frac{1}{k_B T}である。

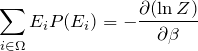
2. まとめ

　分配関数は、相対的な確率を絶対的な確率に規格化するために計算しているに過ぎない。サイコロの例を見てわかるように、その実態はシンプルである。

　と、ここではわかりやすくサイコロの例で見てきましたが、分配関数 Z は統計力学においては非常に重要な量になっています。この Z から熱力学的な量である、ヘルムホルツのエネルギー F やエントロピー S などを求めることができますが、また別の記事でまとめます。


コメントを残す

メールアドレスが公開されることはありません。