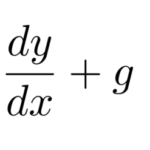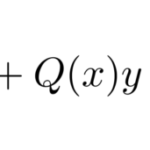ダランベール型(ラグランジュ型)の微分方程式は以下の形をしている。
![]()
![]() のときは、クレローの微分方程式である。 ここでは
のときは、クレローの微分方程式である。 ここでは ![]() の一般的なラグランジュの微分方程式を見ていこう。
の一般的なラグランジュの微分方程式を見ていこう。
次の微分方程式を解け。
![]()
1. ラグランジュ型の微分方程式の解法
ダランベール(ラグランジュ)の微分方程式
![]()
の解き方は以下の3STEP である。
-
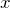 で微分する
で微分する - 1次線形型の微分方程式を解く
- 一般解、特殊解、特異解を調べる
ラグランジュの微分方程式を解く上では、![]() で微分すると線形型に変形できること が重要である。このことを確認して、具体的な例題を解いていくのが良い。 具体的な形がないとかなりわかりにくいと思う。
で微分すると線形型に変形できること が重要である。このことを確認して、具体的な例題を解いていくのが良い。 具体的な形がないとかなりわかりにくいと思う。
*このタイプの微分方程式を学ぶためには、まずクレローの微分方程式の解法を学ばなくてはならない。特に重要な媒介変数表示された一般解の表現についてはクレロー型のところで説明している。
xで微分する
(1) の両辺を ![]() で微分する。
で微分する。
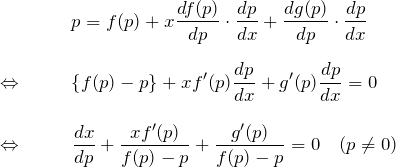
これがどのタイプの微分方程式になるかわかるだろうか。
![]()
と同じ線形型の微分方程式となっている。ここで ![]() に対して
に対して
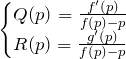
としておく。これは覚えるものではない。実際の問題では、ラグランジュの微分方程式の両辺を ![]() で微分し、線形型の微分方程式に変形していけば良い。
で微分し、線形型の微分方程式に変形していけば良い。
線形型微分方程式を解く
![]()
の線形型に対して、両辺に
![]()
をかけて整理すると
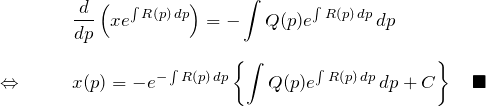
これが一般解である。これもまた覚えるものではない。
ここで得られた形は ![]() を含む(
を含む(![]() は積分定数)式で表される。 これを
は積分定数)式で表される。 これを ![]() としておく。
としておく。
すると、![]() の関係はこの式と(1)で表される。
の関係はこの式と(1)で表される。
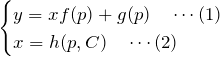
この2式は ![]() が
が ![]() によって表されている、つまり
によって表されている、つまり ![]() を媒介変数とした形になっている。
を媒介変数とした形になっている。![]() の関係は
の関係は ![]() によって結び付けられている。
によって結び付けられている。
したがって、(1)(2)は微分方程式の一般解を媒介変数で表した形になっており、2式から ![]() を消去したものは
を消去したものは ![]() のみで表された一般解になる。
のみで表された一般解になる。
一般解、特殊解、特異解を調べる
最後に一般解、特殊解、特異解を調べる方法を説明する。
一般解
これは上で説明した通りである。 一般解は媒介変数表示で表すと、上の(1)(2)の2式になる。また、![]() を消去した形でも書くことができる。
を消去した形でも書くことができる。
特殊解
上の一般解は ![]() のときのものである。
のときのものである。![]() の解が特殊解に対応する。 すなわち、(1)より特殊解は
の解が特殊解に対応する。 すなわち、(1)より特殊解は
![]()
である。特殊解は適当な ![]() を選ぶことにより一般解に含まれる場合がある。
を選ぶことにより一般解に含まれる場合がある。
特異解
得られた一般解を ![]() で偏微分して得る。クレロー型の場合は特異解は一般解の包絡線になっていたことを思い出す。
で偏微分して得る。クレロー型の場合は特異解は一般解の包絡線になっていたことを思い出す。
特異解がない場合もある(ここで扱う例題など)。
以上のように、ラグランジュの微分方程式では一般解、特殊解、特異解を調べる必要がある。
2. 例題の解答
解き方が複雑なので一通り解答を見て、再度自分で解くことをお勧めする。 特に ![]() の消去する計算は複雑であるし、自分のやり方もあると思う。
の消去する計算は複雑であるし、自分のやり方もあると思う。
【解答】 例題は以下のように書けるラグランジュの微分方程式である。
![]()
一般解
![]() で微分:
で微分:
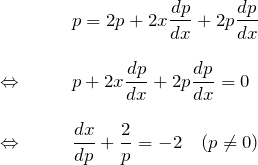
![]() は特殊解である。
は特殊解である。
線形型を解く:
両辺に ![]() をかけて整理すると
をかけて整理すると
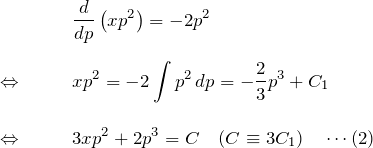
以上より、一般解の媒介変数表示は(1)(2)で表される。
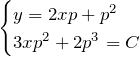
![]() を消去:
を消去:
パラメータの ![]() を消去していく。(1)より
を消去していく。(1)より
![]()
を用いて次数を下げていく。(2)について
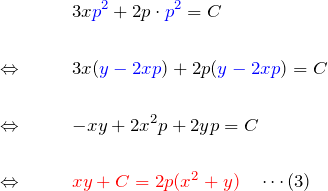
これの両辺を2乗して
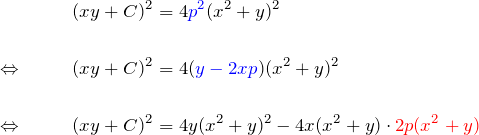
最後の行で、式(3)の形をわかりやすく書いた。(3)を代入して、
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&(xy+C)^2 = 4y(x^2+y)^2 -4x(x^2+y)\textcolor{red}{(xy+C)}\\\\ \Leftrightarrow \quad && (xy+C)^2 = 4(x^2+y)^2\Bigl[y(x^2+y)-x(xy+C)\Bigr]\\\\ \Leftrightarrow \quad && (xy+C)^2 = 4(x^2+y)^2\Bigl[\cancel{x^2y}+y^2-\cancel{x^2y}-Cx)\Bigr]\\\\ \Leftrightarrow \quad && (xy+C)^2 = 4(x^2+y)(y^2-Cx)\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-cf7f4b73a3fe3fea2d305d0266b4f9e4_l3.png)
これが(1)(2)から ![]() を消去して得られる一般解である。
を消去して得られる一般解である。
特殊解
![]() のとき、(1)より
のとき、(1)より ![]() である。このとき、一般解へ代入すると
である。このとき、一般解へ代入すると
![]()
であり、![]() のときの解に対応することがわかる。
したがって、特殊解も含めて
のときの解に対応することがわかる。
したがって、特殊解も含めて
![]()
の形になる。
特異解
一般解の式を ![]() で偏微分して
で偏微分して
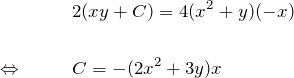
この ![]() を一般解へ代入して
を一般解へ代入して
![]()
を得る。これは(1)を満たさないので、特異解ではない。 したがって特異解はない。
*![]() が(1)を満たさないことは
が(1)を満たさないことは
![]()
を
![]()
へ代入するとわかる。
3. まとめ
とにかくダランベール型(ラグランジュ型)やクレロー型は ![]() で微分してみる。 そうすると線形型の微分方程式が得られて解くことができる。
で微分してみる。 そうすると線形型の微分方程式が得られて解くことができる。
その後、一般解が媒介変数表示で表されているため、![]() を消去して
を消去して ![]() と
と ![]() の関係式が得られる。特殊解、特異解についても調べることを忘れないようにしよう。
の関係式が得られる。特殊解、特異解についても調べることを忘れないようにしよう。