振動は物理において重要な運動である。ここでは摩擦の項がない(減衰のない)強制振動の運動方程式(以下の式)をラグランジアンから導出して、一般解を考える。物理現象としては「共鳴」や「 うなり 」に関係する。
![]()
ここで学ぶ強制振動以外にさまざまな振動がある。
ざっくり言うと、振動数 ![]() の単振動を基礎にして、摩擦や外場などを導入してどうなるか調べることに意味がある。
の単振動を基礎にして、摩擦や外場などを導入してどうなるか調べることに意味がある。
目次
1. 強制振動とは
強制振動は名の通り「強制的」に質点などを振動させる。とくに重要な場合として、もともと質点が振動数 ![]() で単振動している場合に、外場による力
で単振動している場合に、外場による力 ![]() を与えて単振動を変えてしまう。振動している電磁波によって粒子を揺らしたりするような話である。
を与えて単振動を変えてしまう。振動している電磁波によって粒子を揺らしたりするような話である。
単振動の振動数と外場の振動数が同じ場合には振動の振幅は増大する。これが共鳴である。単振動ではないが、ブランコに乗っているひとを後ろから押して振れ幅を大きくするイメージである。
物理現象として粒子などが単振動している場合はよくある。その系を外場によって強制的に振動させるのが強制振動である。ある程度イメージを持っていた方が運動方程式に馴染みやすいだろう。
2. ラグランジアン → 運動方程式
運動方程式の導出をラグランジアンから導く。与えられた運動方程式を解きたい方はスキップしてよい。
はじめに重要な事項を以下にまとめる。
- 仮定:単振動、減衰振動、強制振動において変位
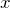 は小さい
は小さい - 系のラグランジアン
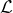 を作る → 運動方程式を作る
を作る → 運動方程式を作る - 外場による力
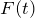 は周期関数
は周期関数
2.1 外場のポテンシャルと力 F(t)
変位 ![]() が小さい場合は外場によるポテンシャル
が小さい場合は外場によるポテンシャル ![]() は 微小量の
は 微小量の ![]() 周りで展開できる。
周りで展開できる。
![]()
第一項:
これは時間 ![]() のみに依存するが、作用
のみに依存するが、作用 ![]() の変分をとるとこの項は消える。したがって、あってもなくてもニュートンの運動方程式の形は変わらない。
の変分をとるとこの項は消える。したがって、あってもなくてもニュートンの運動方程式の形は変わらない。
第二項:
ポテンシャルの位置に関する微分は力になる。つまり ![]() である。この
である。この ![]() は釣り合いの位置で働く外場による力を表す。
は釣り合いの位置で働く外場による力を表す。
※ポテンシャルの微分がピンとこない場合は、クーロン力とそのポテンシャルエネルギーの関係を思い出して納得して欲しい。
2.2 ラグランジアンと運動方程式
単振動について、
- 運動エネルギー:
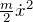
- バネのエネルギー(ポテンシャルエネルギー):
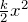
である。これに、外場のポテンシャルを加えてラグランジアン ![]() が求められる。
が求められる。
![]()
これをオイラー・ラグランジュ方程式、
![]()
に代入してニュートンの運動方程式が求められる。
![]()
3. 運動方程式を解く
外場による力 ![]() が振動数
が振動数 ![]() の周期的な関数の場合を考える。
の周期的な関数の場合を考える。
![]()
3.1 微分方程式を解く(ω≠ω0)
非同次線形微分方程式を解くために、まず同次系の単振動の運動方程式 ![]() の解は
の解は ![]() と書く。
と書く。
与えられた非同次線形微分方程式の一般解は ![]() と特殊解
と特殊解 ![]() によって
によって ![]() となる。ここで、特殊解
となる。ここで、特殊解 ![]() の形を、
の形を、![]() より
より ![]() と置いてみる。これを微分方程式に代入して係数
と置いてみる。これを微分方程式に代入して係数 ![]() を求めると、
を求めると、
![]()
となる。したがって一般解は、
![]()
になる。![]() は任意の定数である。
は任意の定数である。
強制振動の一般解は以下の振動を重ね合わせたものになる。
- 元の単振動の固有振動数
 による振動
による振動 - 外場の振動の振動数
 と同じ振動数をもつ振動
と同じ振動数をもつ振動
3.2 共鳴する場合(ω=ω0)
外場の振動数 ![]() が単振動の振動数
が単振動の振動数 ![]() と同じである共鳴のときを考える。共鳴に対応する
と同じである共鳴のときを考える。共鳴に対応する ![]() の場合は解は上で求めた一般解だと発散してしまう。
の場合は解は上で求めた一般解だと発散してしまう。
任意定数 ![]() をうまく取り直して、
をうまく取り直して、
![]()
を作る。![]() とするので、
とするので、![]() を
を ![]() 周りで展開する。1次までとると、
周りで展開する。1次までとると、
![]()
となり、![]() において
において
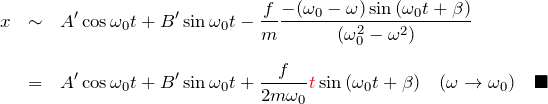
となる。極限の計算は ![]() の展開を使わずにロピタルの定理を用いても良い。
の展開を使わずにロピタルの定理を用いても良い。
元の強制振動の微分方程式が成立する変位の小さい振動においては、![]() の一般解
の一般解 ![]() は上のようになる。この仮定の中で、第二項は時間
は上のようになる。この仮定の中で、第二項は時間 ![]() に対して線形に増加している(これが共鳴)。
に対して線形に増加している(これが共鳴)。
4. まとめ
![]() を 位相
を 位相 ![]() と 定数
と 定数 ![]() で書き直して、強制振動の一般解を表しておく。
で書き直して、強制振動の一般解を表しておく。
![]()
さまざまな振動のうち、強制振動を扱った。強制振動は共鳴と非常に関わりがある振動で、物理的に重要な意味を持つ。また、共鳴の振動数に近い場合は「「 うなり 」」がおこる。
導出はラグランジアンから出発して、運動方程式を求めるところからおこなった。非同次型の微分方程式の解き方を習熟している方にとっては難しい問題ではないと思われる。