減衰振動は自由振動(単振動)の運動に、摩擦による抵抗の項を加えた運動になっている。減衰振動においては、振動の振幅がどんどん小さくなっていき最後には止まってしまう。
また、他の振動と同じく、変位 ![]() が小さい振動(微小振動)のときが重要である。よくある振動の種類は下にまとめた。
が小さい振動(微小振動)のときが重要である。よくある振動の種類は下にまとめた。
- 自由振動(単振動):
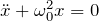
- 減衰振動:
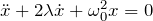
- 強制振動(摩擦無し):
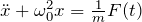
- 強制振動(摩擦あり):
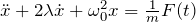
- 非調和振動:(非線形の微分方程式)
目次
1. 運動方程式
微小振動の場合は、摩擦は速度に比例すると近似できる。
![]()
比例定数 ![]() は正の値をとり、大きいほど摩擦による抵抗が大きい。運動を妨げる方向に働くために速度と逆符号(マイナス)になっている。
は正の値をとり、大きいほど摩擦による抵抗が大きい。運動を妨げる方向に働くために速度と逆符号(マイナス)になっている。
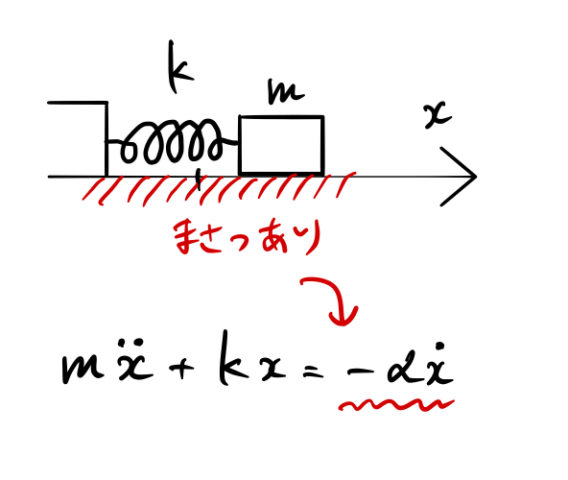
この摩擦力を自由振動の運動方程式の右辺に加えてやれば良い。
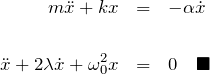
項の説明:
- 摩擦がない時の自由振動の振動数:
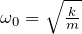
- 減衰率:
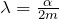
2. 一般解
2階の線形微分方程式を解く(解き方)。まず ![]() と置いて上の運動方程式に代入する。
と置いて上の運動方程式に代入する。
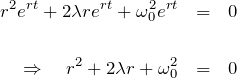
のように特性方程式を得る。2次方程式の解の公式より、2つの解を ![]() として
として
![]()
である。
したがって一般解は、
![]()
になる。後は ![]() がどうなるか場合分けしてみていく。
がどうなるか場合分けしてみていく。
2.1 λ<ω0 のとき(減衰振動; under damping)
![]() の複素数である。
の複素数である。
一般解 ![]() を変形する(丁寧めに):
を変形する(丁寧めに):
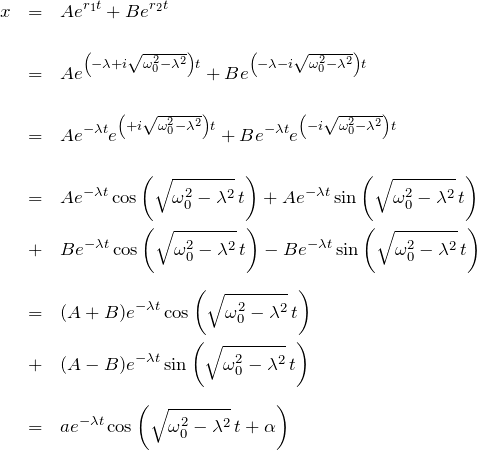
- オイラーの公式:
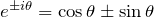
 の和を
の和を 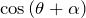 で表す
で表す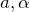 :定数
:定数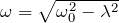 :減衰振動の振動数(
:減衰振動の振動数(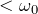 )
)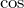 の振幅を
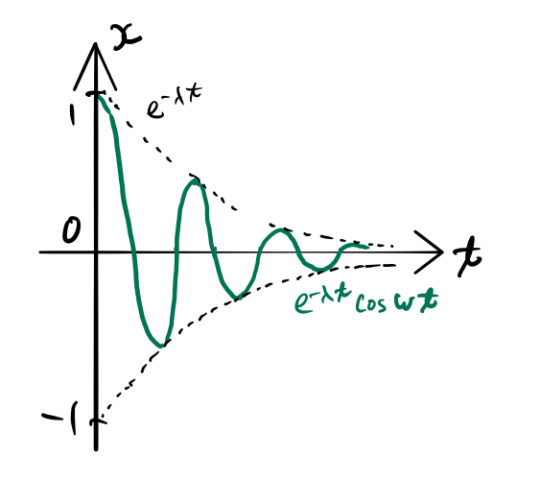
の振幅を 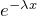 で指数関数的に減少させる(下図)
で指数関数的に減少させる(下図)
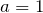 , 初期位相
, 初期位相 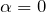 とした。減衰振動は振幅がだんだん小さくなっていく振動である。
とした。減衰振動は振幅がだんだん小さくなっていく振動である。 ![]() により、振動の振幅は
により、振動の振幅は ![]() が大きくなるにつれて大きく減衰していく。
が大きくなるにつれて大きく減衰していく。
2.2 λ=ω0 のとき(臨界減衰; critical damping)
![]() (重解)である。
(重解)である。
2階微分方程式における特性方程式が重解をもつときの一般解は、
![]()
になる。
- この解には三角関数が含まれていない
- 臨界減衰と呼ぶ
- 振動的な解ではない(下図)
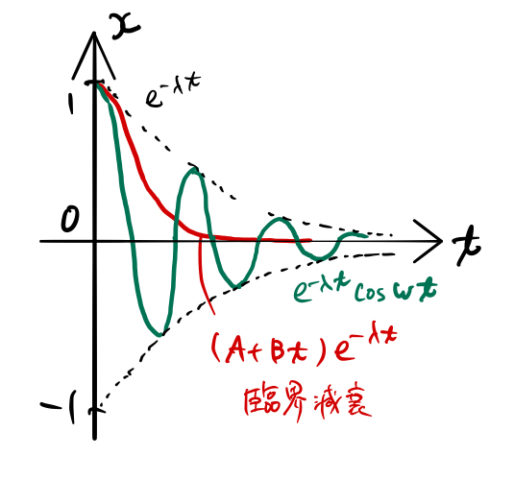
摩擦がない場合は、バネにつけた物体を釣り合いの位置から伸ばして離すと振動する。「摩擦がちょうどいい(臨界)」の場合だと、バネが縮んだ状態にならずに釣り合いの位置に戻る。次の過減衰と同じく、粘性が大きい液体の中でバネを伸ばした場合をイメージすれば良い。
2.3 λ>ω0 のとき(過減衰; over damping)
臨界減衰の場合よりもっと減衰率が大きい場合(摩擦が十分大きい場合)は過減衰になる。
運動方程式の一般解:
![]()
- 過減衰と呼ぶ
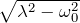 > 0 なので指数関数的な減衰が大きい
> 0 なので指数関数的な減衰が大きい- 摩擦が大きいのでゆっくりと漸近的に釣り合いの位置に戻る
- 一般解に三角関数はない → 振動的な解ではない(下図)
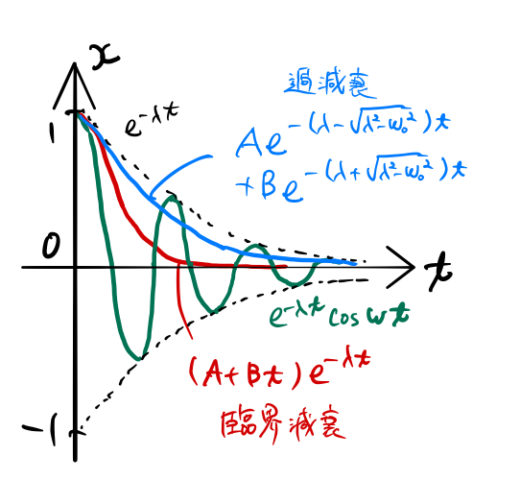
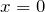 に近づく。
に近づく。 摩擦が十分大きいと釣り合いの位置まで戻るのに時間がかかる。つまり ![]() のように漸近的に
のように漸近的に ![]() に近づく。臨界減衰と同じく、かなり粘性が大きい液体の中でバネを伸ばした場合をイメージすれば良い。
に近づく。臨界減衰と同じく、かなり粘性が大きい液体の中でバネを伸ばした場合をイメージすれば良い。
3. 減衰振動のデモンストレーション動画
減衰振動の様子がめちゃめちゃわかりやすい動画があったので紹介する。2:30秒から under damping, critical damping, over damping をまとめて再生している。
導体であるアルミニウムを近づけて、ものさしの先につけた磁石の振り子の振動を見ている。アルミニウムの壁が近いほど減衰率は大きくなります。詳しい説明は 本家のページで(英語版) 。
琴線に触れる動画である。実際に琴線に触れてるような音も聞こえる。
4. まとめ
減衰振動の問題は微分方程式と関わりがあるため、数学に慣れてないと難しいのかもしれない。この減衰振動の話はRLC回路のところでも出てくる。
数式で一般解を求めた後に、最後の動画をみると感動しませんか。