例題を使って微分方程式の初期値問題をラプラス変換で解く。 初期値が与えられている微分方程式はラプラス変換によってをかんたんに解くことができる。 ここでは下の例題のような単純な斉次線形微分方程式を解いていく(非斉次微分方程式のラプラス変換による解法は こちら )。
以下の![]() に関する微分方程式をラプラス変換を用いて解け。ただし初期値は
に関する微分方程式をラプラス変換を用いて解け。ただし初期値は![]() とする。
とする。
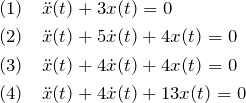
目次
1. ラプラス変換・逆変換の基本事項
基本事項をざっと復習する。
微分のラプラス変換
微分方程式をラプラス変換で解く上で大事な ![]() のラプラス変換を簡単にまとめる。
のラプラス変換を簡単にまとめる。
1回微分のラプラス変換:部分積分する
&=&\int_0^{\infty}x'(t)e^{-st}\,dt\\\\ &=&\left[x(t)e^{-st}\right]_0^{\infty}-(-s)\int_0^{\infty}x(t)e^{-st}\,dt\\\\ &=&-x(0)+sX(s)\quad(X(s)\equiv{\mathcal L}[x(t)](s))\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8f5df95a574cd642f54796f96a9b6b29_l3.png)
2回微分のラプラス変換:上の結果を使う(![]() と置き換える)
と置き換える)
 &=&-x'(0)+s\textcolor{red}{\tilde{X}(s)} \quad(\textcolor{red}{\tilde{X}(s)}\equiv{\mathcal L}[x'(t)](s))\\\\ &=&-x'(0)+s\left[\textcolor{red}{-x(0)+sX(s)}\right] \quad(X(s)\equiv{\mathcalL}[x(t)](s))\\\\ &=&-x'(0)+sx(0)+s^2X(s)\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-75346e4ca9da455fa7ecf0b25e072a22_l3.png)
s移動を用いたラプラス逆変換
![]() 移動について簡単にまとめる。以下では「⇒」をラプラス逆変換とする。
移動について簡単にまとめる。以下では「⇒」をラプラス逆変換とする。
![]()
に対して
![]()
例えば、
![]()
である。
2. 解答
以下の解答では![]() のラプラス変換を
のラプラス変換を ![]() とする。 また、与えられた初期値は
とする。 また、与えられた初期値は ![]() である。
である。
例題(1)の解答
与えられた微分方程式の両辺をラプラス変換すると
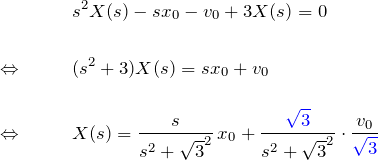
![]() のラプラス逆変換が使えるように
のラプラス逆変換が使えるように ![]() とした。 最後の行を「
とした。 最後の行を「![]() 移動」を用いてラプラス逆変換すると
移動」を用いてラプラス逆変換すると
![]()
※ここで ![]() と考えても同じ結果になる。つまり、
と考えても同じ結果になる。つまり、
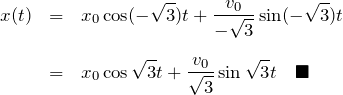
例題(2)の解答
与えられた微分方程式の両辺をラプラス変換すると
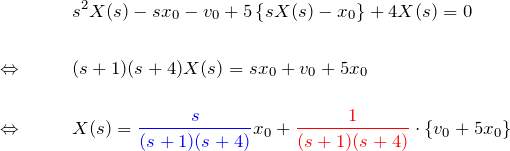
ここで、部分分数分解
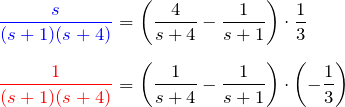
を用いて、
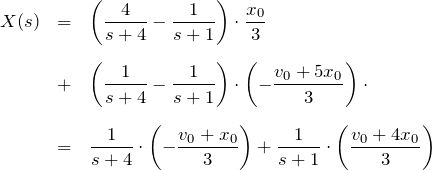
となる。![]() と
と ![]() に対して「
に対して「![]() 移動」を用いたラプラス逆変換をおこなうと、
移動」を用いたラプラス逆変換をおこなうと、
![]()
例題(3)の解答
与えられた微分方程式の両辺をラプラス変換すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&s^2X(s)-sx_0-v_0+4\left\{sX(s)-x_0\right\}+4X(s)=0\\\\ \Leftrightarrow\quad&& (s+2)^2X(s)=sx_0+v_0+4x_0\\\\ \Leftrightarrow\quad&& X(s)=\textcolor{blue}{\frac{1}{(s+2)^2}}x_0 +\frac{1}{(s+2)^2}\cdot\left\{v_0+4x_0\right\}\\\\ \Leftrightarrow\quad&& \textcolor{blue}{\left[\frac{1}{s+2}-\frac{2}{(s+2)^2}\right]}x_0 +\frac{1}{(s+2)^2}\left\{v_0+4x_0\right\}\\\\ \Leftrightarrow\quad&& \frac{x_0}{s+2}+\frac{v_0+2x_0}{(s+2)^2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-bc833c77133d20ba21db4099247a0600_l3.png)
「![]() 移動」を用いてラプラス逆変換すると、
移動」を用いてラプラス逆変換すると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} x(t) &=&x_0e^{-2t}+\left(v_0+2x_0\right)\,te^{-2t}\\\\ &=&\Bigl[x_0+(v_0+2x_0)t\Bigr]e^{-2t}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-64225335b06d7655105304bc5b5f2554_l3.png)
例題(4)の解答
与えられた微分方程式の両辺をラプラス変換すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&s^2X(s)-sx_0-v_0+4\left\{sX(s)-x_0\right\}+13X(s)=0\\\\ \Leftrightarrow\quad&& (s^2+4s+13)X(s)=sx_0+v_0+4x_0\\\\ \Leftrightarrow\quad&& \Bigl[(s+2)^2+3^2\Bigr]X(s)=sx_0+v_0+4x_0\\\\ \Leftrightarrow\quad&& X(s)=\frac{s}{(s+2)^2+3^2}x_0+\frac{v_0+4x_0}{(s+2)^2+3^2}\\\\ \Leftrightarrow\quad&& X(s)=\frac{\textcolor{red}{(s+2)}-2}{(s+2)^2+3^2}x_0 +\frac{v_0+4x_0}{(s+2)^2+3^2}\\\\ \Leftrightarrow\quad&& X(s)=\frac{\textcolor{red}{(s+2)}}{(s+2)^2+3^2} x_0+\frac{v_0+2x_0}{(s+2)^2+3^2}\\\\ \Leftrightarrow\quad&& X(s)=\frac{\textcolor{red}{(s+2)}}{(s+2)^2+3^2}x_0 +\frac{\textcolor{blue}{3}}{(s+2)^2+3^2}\cdot \frac{v_0+2x_0}{\textcolor{blue}{3}} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b220d297f2bf9ef1daae5f21a4bb873f_l3.png)
「![]() 移動」と
移動」と![]() のラプラス変換(逆変換)より、
のラプラス変換(逆変換)より、
![]()
3. これらの解の物理的意味
得られた解について簡単に触れておく。 (1)から(4)の微分方程式は振動の運動方程式と関係する。
(1)は1次元の単振動(自由振動)を表す運動方程式である。 したがって得られた解は
![]()
のように初期位相 ![]() と振幅
と振幅 ![]() で表すことができる。
で表すことができる。
(2)(3)(4)の微分方程式に含まれる ![]() の項は 係数が0より大きいため摩擦項に対応する(下図)。
の項は 係数が0より大きいため摩擦項に対応する(下図)。
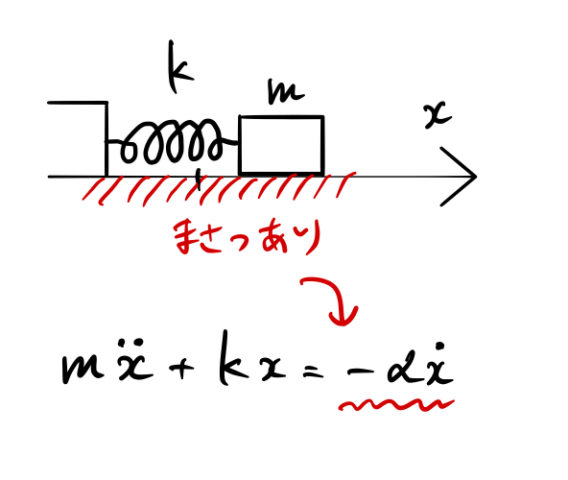
それぞれ、![]() の係数と
の係数と ![]() の係数の関係より解の意味が異なる。 (2)の解はもはや振動的な解ではない。これは過減衰(over damping)に対応する運動である。 (3)の解は臨界減衰(critical damping)に対応する。 (4)の解は三角関数の振動的性質の残った減衰振動(under damping)である。 これは解を
の係数の関係より解の意味が異なる。 (2)の解はもはや振動的な解ではない。これは過減衰(over damping)に対応する運動である。 (3)の解は臨界減衰(critical damping)に対応する。 (4)の解は三角関数の振動的性質の残った減衰振動(under damping)である。 これは解を
![]()
と書いてみればわかる。
4. まとめ
一般に、ここで挙げた4タイプは以下のように分類できる。
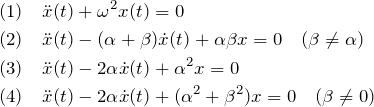
一般的には、![]() と
と ![]() の組み合わせによって、上のように過減衰、減衰振動、臨界振動の解にならないことがある。
の組み合わせによって、上のように過減衰、減衰振動、臨界振動の解にならないことがある。
また、本例題の微分方程式はラプラス変換を使わなくても解くことができる。![]() とおいて特性方程式を作って解くやり方などがある。この方法は力学の教科書にも載っている よくある解き方になる。
とおいて特性方程式を作って解くやり方などがある。この方法は力学の教科書にも載っている よくある解き方になる。
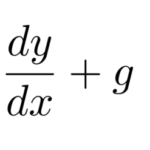
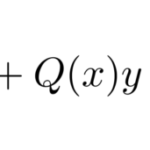
ボケ防止目的で頭の運動のため利用させていただいておりありがとうございます。
例題4の回答のCos3tの係数にX0を掛ける必要がありませんでしょうか?
私の計算ミスであれば申し訳ありません。
係数x0は必要です。途中式で消えていたようです。
ご指摘ありがとうございました。