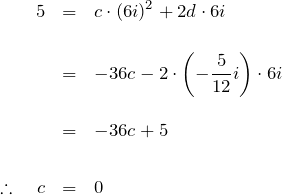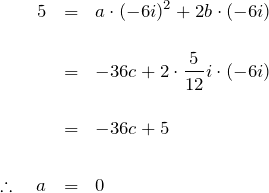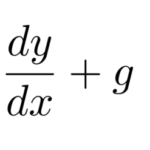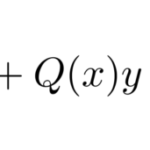前回はラプラス変換を用いた斉次線形微分方程式を扱った。 ここでは例題を通して非斉次の線形微分方程式を解いていく。 例題(1)は斉次、(2)(3)(4)は非斉次の微分方程式である。
次の ![]() に関する微分方程式を解け。 ただし初期値は
に関する微分方程式を解け。 ただし初期値は ![]() ,
, ![]() とする。
とする。
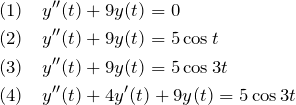
1. 基礎事項について
を使うため、 これらの内容が不十分であれば一度戻って復習しないといけない。
2. 例題の解答
ラプラス変換による微分方程式の解法は、 まず微分方程式をラプラス変換するところから始める。
以下では、求める ![]() のラプラス変換を
のラプラス変換を ![]() とする。
初期値は
とする。
初期値は ![]() ,
, ![]() である。
である。
例題(1)の解答
(1)で表された斉次の線形微分方程式(単振動の運動方程式など)を解いていく。
【解答】
微分方程式の両辺をラプラス変換する。微分のラプラス変換を用いて、
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&s^2 Y(s) -sy_0 - v_0 + 9Y(s)=0\\\\ \Leftrightarrow\quad&& Y(s)=\frac{s}{s^2+9}y_0 + \frac{\textcolor{blue}{3}}{s^2 + 9}\cdot\frac{v_0}{\textcolor{blue}{3}}\\\\ \therefore\quad&&y(t)={\mathcal L}^{-1}[Y(s)]=y_0\cos 3t + \frac{v_0}{3}\sin 3t \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4612b951f6b28c3650787352f0d3f431_l3.png)
となる。
解を ![]() と書けば、単振動を表すことがわかる(
と書けば、単振動を表すことがわかる(![]() は初期位相)。
は初期位相)。
例題(2)の解答
(2)は非斉次の線形微分方程式であり、(強制振動の運動方程式など)を表す。
【解答】
微分方程式の両辺をラプラス変換する。 微分のラプラス変換と ![]() のラプラス変換を用いる。 このとき左辺は例題(1)と同様の形になる。
のラプラス変換を用いる。 このとき左辺は例題(1)と同様の形になる。
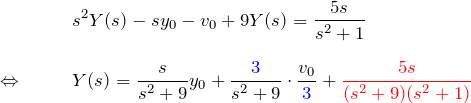
ここで、第3項について部分分数分解
![]()
を用いて、
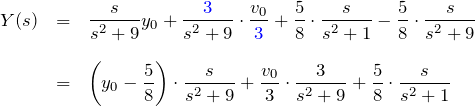
を得る。これをラプラス逆変換して微分方程式の解を得る。
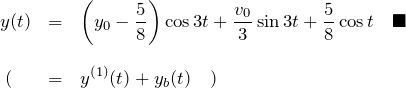
ここで、![]() は例題(1)の解と同じ形の斉次解である
(初期値を同じにしたため
は例題(1)の解と同じ形の斉次解である
(初期値を同じにしたため ![]() の係数が異なる)。
の係数が異なる)。
![]() は特殊解を表す。
非斉次微分方程式の一般解は、(斉次解)+(特殊解)の形になる。
例題(2)で初期値が与えられていない場合の一般解は、
は特殊解を表す。
非斉次微分方程式の一般解は、(斉次解)+(特殊解)の形になる。
例題(2)で初期値が与えられていない場合の一般解は、
![]()
となる。
例題(3)の解答
例題(2)と似ているがどうだろうか。
【解答】
微分方程式の両辺をラプラス変換する。
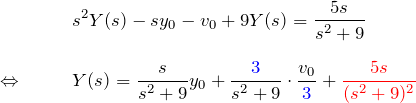
ここで、第3項について部分分数分解する。
![]() と因数分解して
と因数分解して
![]()
と置き、係数 ![]() を求めると、
を求めると、
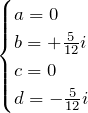
である。したがって、
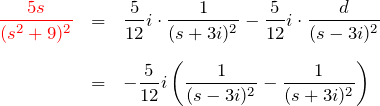
ここで「![]() 移動」によるラプラス逆変換:
移動」によるラプラス逆変換:
![]()
を用いて、
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}^{-1} \left[ \frac{5s}{(s^2+9)^2}\right] &=&-\frac{5}{12}i\cdot t\left(e^{3it}-e^{-3it}\right)\\\\ &=&-\frac{5}{12}i\cdot t\cdot 2i\sin 3t\\\\ &=&+\frac{5}{6}t\sin 3t \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ad8c01367530b1927d0b1437b6a66978_l3.png)
したがって、
![]()
をラプラス逆変換して微分方程式の解を得る。
![]()
※解は ![]() が大きくなると第三項により振動の振幅が増幅する。 もともとの微分方程式の左辺は単振動の運動方程式であり、 右辺を時間
が大きくなると第三項により振動の振幅が増幅する。 もともとの微分方程式の左辺は単振動の運動方程式であり、 右辺を時間 ![]() で振動する外力とみると、 外力の振動数と元の単振動の振動数が一致している。 これは「共鳴」であり、振幅が増幅していることに対応する。
で振動する外力とみると、 外力の振動数と元の単振動の振動数が一致している。 これは「共鳴」であり、振幅が増幅していることに対応する。
例題(4)の解答
【解答】
微分方程式の両辺をラプラス変換する
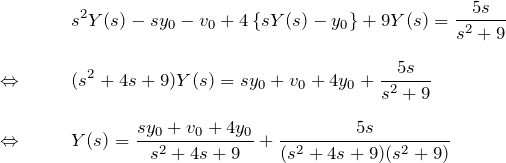
第一項について:
![]()
を利用して
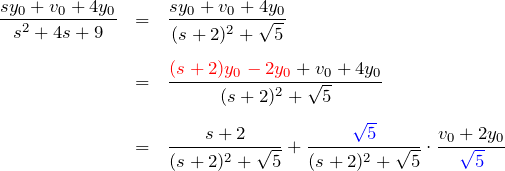
第二項について:
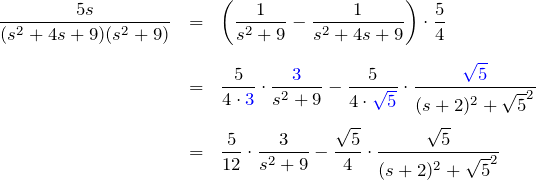
したがって、
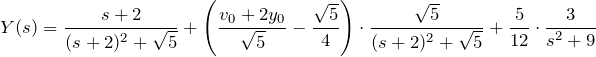
「![]() 移動」および
移動」および ![]() のラプラス逆変換により
のラプラス逆変換により
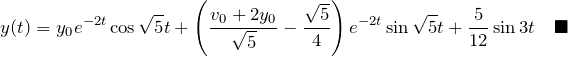
*第一項と第二項は
![]() の形の減衰振動を表す。
第三項は強制振動による振動運動を表している。
の形の減衰振動を表す。
第三項は強制振動による振動運動を表している。
まとめ
ここでは非斉次の微分方程式をラプラス変換により解いてきた。 方程式の形として単振動や強制振動の形を扱った。ラプラス変換の応用として微分方程式を解いてきたが、本例題はよくある方法でも解くことができる。