以下のヘヴィサイドの単位関数は応用上重要である。 ここでは単位関数について簡単に説明し、そのラプラス変換について学ぶ。
次の ![]() に関する関数をラプラス逆変換して
に関する関数をラプラス逆変換して ![]() を求めよ。 また、
を求めよ。 また、![]() を図示せよ。
を図示せよ。
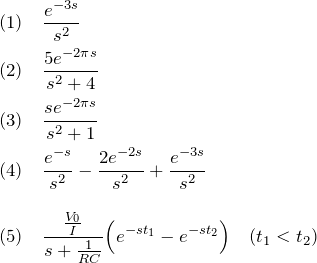
目次
1. ヘヴィサイドの階段関数
階段関数の定義
ヘヴィサイドの階段関数(Heaviside step function)![]() は以下の値をもつ。
は以下の値をもつ。
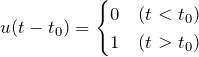
![]() で1にジャンプする。
で1にジャンプする。
![]() で不連続な関数であるため、
で不連続な関数であるため、![]() で値を定義した単位ステップ関数もある。
で値を定義した単位ステップ関数もある。
なぜ必要であるか
階段関数はある時間で値が0から1になる関数である。 1/0の値は電源スイッチなどのON/OFFに対応していると言える。
例えば、ある関数 ![]() を用意する。 この関数と階段関数を用いて
を用意する。 この関数と階段関数を用いて ![]() のON/OFFを関数として表現できる。
のON/OFFを関数として表現できる。
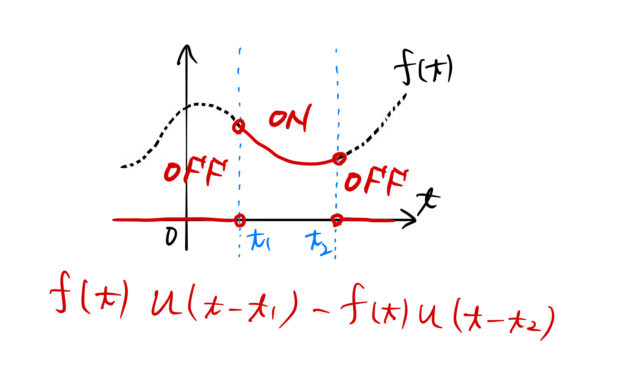
物理現象を関数として表現できれば、 解析的に微分・積分を実行することが可能である。 したがって、階段関数は非常に便利である。 微分方程式をラプラス変換を用いて解く場合にも、 階段関数が便利であるとわかるだろう。
組み合わせて使う
階段関数を ![]() と組み合わせて新たな関数を作ることができる。
と組み合わせて新たな関数を作ることができる。
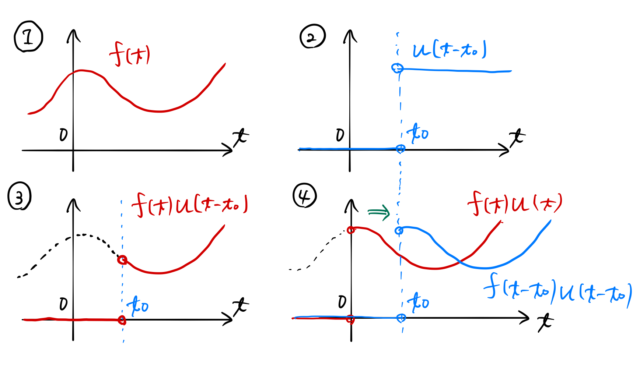
① 関数 ![]() と② 階段関数
と② 階段関数 ![]() である。 ④ は
である。 ④ は ![]() で、ある外場による力
で、ある外場による力 ![]() をかけ始めることなどに対応する。
をかけ始めることなどに対応する。
2. ラプラス変換/逆変換
以下の性質を証明する。
 =\frac{e^{-st_0}}{s}\\\\ \square\quad&& {\mathcal L}\left[f(t-t_0)u(t-t_0)\right](s)=e^{-st_0}F(s)\\\\ \square\quad&& {\mathcal L}^{-1}\left[e^{-st_0}F(s)\right](t)=f(t-t_0)u(t-t_0) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8ff16d250ff54b03fb593c9a1350760c_l3.png)
単位関数のラプラス変換
計算の方針:定義通り計算する。
 &=&\int_0^{\infty} u(t-t_0)e^{-st}\, dt\\\\ &=&\int_{\textcolor{red}{t_0}}^{\infty} {\bf 1}\,e^{-st}\, dt\\\\ &=&\left[-\frac{1}{s}e^{-st}\right]_{t_0}^{\infty}\\\\ &=&\frac{e^{-st_0}}{s}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-52867962052ac455c67a7086247abceb_l3.png)
f(t-t0)u(t-t0)のラプラス変換/逆変換【tシフト】
計算の方針:定義通り計算する。
 &=&\int_0^{\infty}f(t-t_0)u(t-t_0)e^{-st}\,dt\\\\ &=&\int_{\textcolor{red}{t_0}}^{\infty}f(t-t_0)\,{\bf 1}\,e^{-st}\,dt\\\\ &=&\int_{0}^{\infty}f(\tau)e^{-s(\tau+t_0)}\,d\tau\quad(\tau=t-t_0)\\\\ &=&e^{-st_0}\int_0^{\infty}f(\tau)e^{-s\tau}d\tau\\\\ &=&e^{-st_0}F(s)\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ee6410cfb1f1ae3abe7666fede2d9bde_l3.png)
ここで、![]() は
は ![]() のラプラス変換である。したがって、ラプラス逆変換は
のラプラス変換である。したがって、ラプラス逆変換は
![]()
となる。この逆変換が、ラプラス変換で微分方程式を解くときに現れることがある。
3. 例題の解答
![]() 移動を使う上での方針:
移動を使う上での方針:
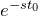 を除く
を除く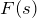 のラプラス逆変換した
のラプラス逆変換した 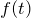 を考える
を考える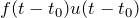 と書く
と書く- グラフは
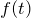 を
を 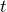 移動して
移動して  は0にする
は0にする
本例題の逆変換で重要なポイントは以下の通り。
![]()
その他、通常のラプラス逆変換はできる前提である(逆変換表まとめ)。
例題(1)の解答
【解答】
1. ![]() を除く:
を除く:
![]()
2. ![]() のラプラス逆変換:
のラプラス逆変換:
![]()
3. ![]() と書く:
と書く:
 &=&f(t-3)u(t-3)\\\\ &=&(t-3)u(t-3)\\\\ &=&\begin{cases} 0 \quad(t < 3)\\ t-3\quad(3>t) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-03fd1bb0948c1c67fb64a2ab1a13e928_l3.png)
4. グラフを描く
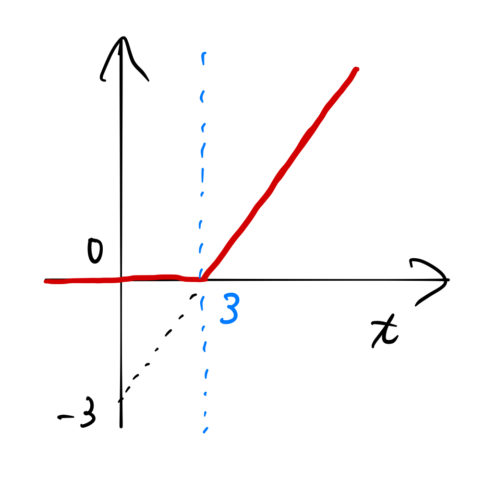
例題(2)の解答
【解答】
1. ![]() を除く:
を除く:
![]()
2. ![]() のラプラス逆変換:
のラプラス逆変換:
 &=& \frac{5}{\textcolor{blue}{2}}{\mathcal L}^{-1}\left[\frac{\textcolor{blue}{2}}{s^2+4}\right](t)\\\\ &=& \frac{5}{2}\sin 2t \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ebff91a36f450b93950d2de59eb44bf1_l3.png)
3. ![]() と書く:
と書く:
 &=&f(t-2\pi)u(t-2\pi)\\\\ &=&\frac{5}{2}\sin[2(t-2\pi)]\,u(t-2\pi)\\\\ &=&\begin{cases} 0 \quad(t < 2\pi)\\\\ \frac{5}{2}\sin[2(t-2\pi)]=\frac{5}{2}\sin 2t\quad(2\pi>t) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a16626045a60dfdfec9e57469a3fc9ad_l3.png)
4. グラフを描く
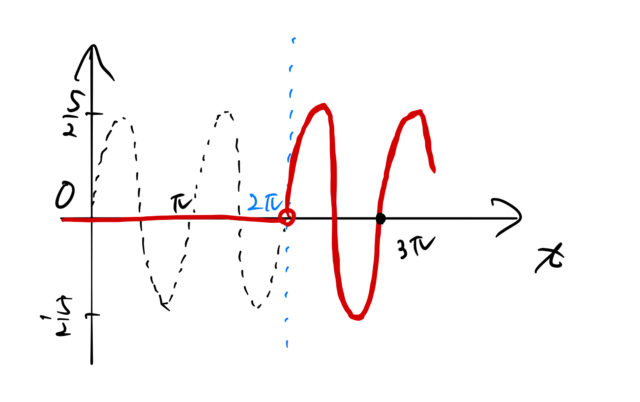
![]() は周期
は周期 ![]() の関数である。
の関数である。
例題(3)の解答
【解答】
1. ![]() を除く:
を除く:
![]()
2. ![]() のラプラス逆変換:
のラプラス逆変換:
![]()
3. ![]() と書く:
と書く:
 &=&f(t-2\pi)u(t-2\pi)\\\\ &=&\cos(t-2\pi)u(t-2\pi)\\\\ &=& \begin{cases} 0 \quad(t < 2\pi)\\\\ \cos(t-2\pi)=\cos t\quad(2\pi>t) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-7729e2eab08482c40169ff96d68eb0f4_l3.png)
4. グラフを描く
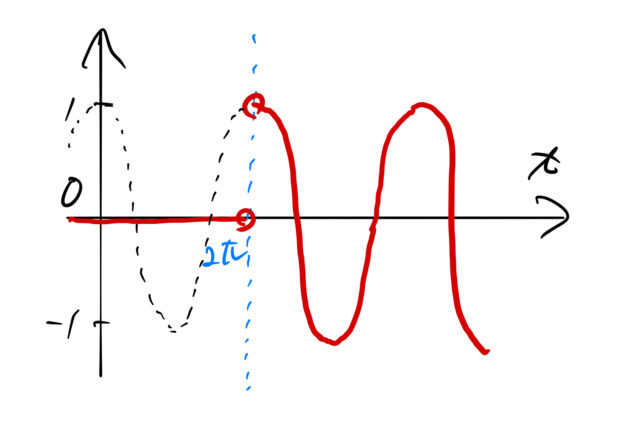
![]() は周期
は周期 ![]() の関数である。
の関数である。
例題(4)の解答
例題(1)と同様のラプラス逆変換を3つの項についておこなう。
【解答】
![]()
より。それぞれの項についてラプラス逆変換すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} {\mathcal L}^{-1}\left[\frac{e^{-s}}{s^2}\right]=(t-1)u(t-1)\\\\ -2{\mathcal L}^{-1}\left[\frac{e^{-s}}{s^2}\right]=-2(t-2)u(t-2)\\\\ {\mathcal L}^{-1}\left[\frac{e^{-s}}{s^2}\right]=(t-3)u(t-3) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-33adf1ec2822194d80a6856341d3a514_l3.png)
したがって
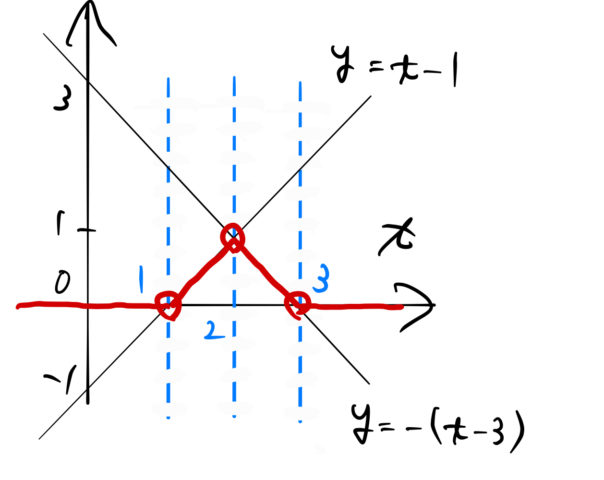
\\\\ &=&(t-1)u(t-1)-2(t-2)u(t-2)+(t-3)u(t-3)\\\\ &=&\begin{cases} 0 \quad(t < 1)\\\\ (t-1)\quad(1 < t < 2)\\\\ -(t-3)\quad(2 < t < 3)\\\\ 0 \quad(3 < t) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2a0224adefc521e83f3aed7ed897648a_l3.png)
このグラフは下図のようになる。
例題(5)の解答
![]() のラプラス逆変換には「
のラプラス逆変換には「![]() 移動(
移動(![]() -shifting)」を使う。
-shifting)」を使う。
【解答】 与えられた関数を
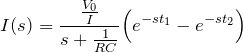
とおく。
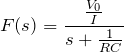
について、
![]()
したがって、与えられた関数のラプラス逆変換は
\\\\ &=&{\mathcal L}^{-s}\left[e^{-st_1}F(s)-e^{-st_2}F(s)\right]\\\\ &=&f(t-t_1)u(t-t_1)-f(t-t_2)u(t-t_2)\\\\ &=&\frac{V_0}{I}e^{-\frac{t-t_1}{RC}}u(t-t_2)-\frac{V_0}{I}e^{-\frac{t-t_2}{RC}}u(t-t_2)\\\\ &=&\frac{V_0}{I}e^{-\frac{t}{RC}}\left\{ e^{\frac{t_1}{RC}}u(t-t_1)-e^{\frac{t_2}{RC}}u(t-t_2)\right\}\\\\ &=&\begin{cases} 0\quad(t < t_1)\\\\ \frac{V_0}{I}e^{-\frac{t}{RC}} e^{\frac{t_1}{RC}}\quad(t_1 < t < t_2)\\\\ \frac{V_0}{I}e^{-\frac{t}{RC}}\left\{ e^{\frac{t_1}{RC}}-e^{\frac{t_2}{RC}} \right\} \quad(t_2 < t) \end{cases}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-caa0cd0d872082832a0a2449f391053e_l3.png)
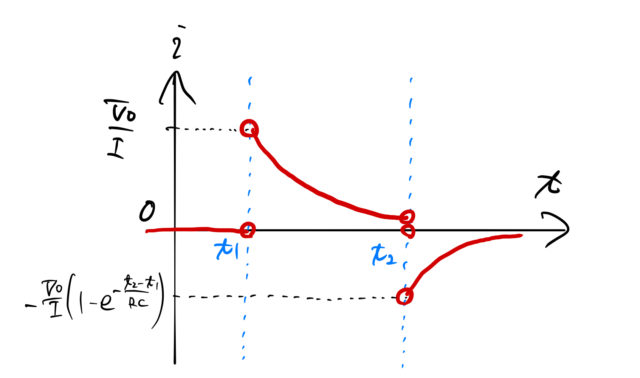
4. まとめ
階段関数とラプラス変換について、その重要性を簡単に説明した。 RC回路などの微分方程式をラプラス変換で解くときには、例題の(5)のようなものが現れる。 ラプラス逆変換に階段関数が現れる(![]() 移動)については計算できるようにしておきたい。
移動)については計算できるようにしておきたい。
例題1の分母はsですか、それともs^2ですか。
解説の方でいきなりs^2がでてきたので疑問に思い質問させていただきました。
すみません、例題が間違っていました。2乗だと思って解答しています。
(分母がsのときの答えは u(t-3) です。
u(t-3) = 0 (t<3), 1 (3