時間 ![]() 世界と
世界と ![]() 世界の往来。変換表とその証明をまとめる。デルタ関数については別に証明するためここには載せなかった。その他の証明は以下の定義でひたすら計算するが、三角関数を含むものはちょっとしたコツがある。
世界の往来。変換表とその証明をまとめる。デルタ関数については別に証明するためここには載せなかった。その他の証明は以下の定義でひたすら計算するが、三角関数を含むものはちょっとしたコツがある。
![]()
これと以下の重要事項でラプラス変換は9割終わる。
1. 証明まとめ
それぞれのラプラス変換の証明と積分が収束するための ![]() の条件を書く。以下で
の条件を書く。以下で ![]() は
は ![]() の実部
の実部 ![]() の意味である。
の意味である。
1
方針:普通に積分する
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} 1\cdot e^{-st} \, dt\\\\ &=& \left[\frac{e^{-st}}{-s}\right]_0^{\infty}\\\\ &=&0-\left(-\frac{1}{s}\right)\\\\ &=&\frac{1}{s}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-64166f779360eaa4c650da9536e2732d_l3.png)
収束: ![]()
t
方針:部分積分を用いる。1のラプラス変換の結果を用いる(赤色部分)。
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} t e^{-st} \, dt\\\\ &=& \int_0^{\infty} t \left(\frac{e^{-st}}{-s}\rigth)' \, dt\\\\ &=& \left[ t\frac{e^{-st}}{-s}\right]_0^{\infty} +\frac{1}{s}\textcolor{red}{\int_0^\infty 1\cdot e^{-st}\, dt}\\\\ &=& 0+\frac{1}{s}\cdot\textcolor{red}{\frac{1}{s}}\\\\ &=&\frac{1}{s^2}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-22980ffbcd850107e301f2b39e5d450b_l3.png)
収束: ![]()
t^2
方針:部分積分を用いる。![]() のラプラス変換の結果を用いる(赤色部分)。
のラプラス変換の結果を用いる(赤色部分)。
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} t^2 e^{-st} \, dt\\\\ &=& \int_0^{\infty} t^2 \left(\frac{e^{-st}}{-s}\rigth)' \, dt\\\\ &=& \left[ t^2\frac{e^{-st}}{-s}\right]_0^{\infty} +\frac{1}{s}\int_0^\infty (t^2)'\,e^{-st}\, dt\\\\ &=& \left[ t^2\frac{e^{-st}}{-s}\right]_0^{\infty} +\frac{2}{s}\textcolor{red}{\int_0^\infty t\cdot e^{-st}\, dt}\\\\ &=& 0+\frac{2}{s}\cdot\textcolor{red}{\frac{1}{s^2}}\\\\ &=&\frac{2}{s^3}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-bfe8a448237dc0a12cbd7fe4429aa3d5_l3.png)
収束: ![]()
t^3
方針:部分積分を用いる。![]() のラプラス変換の結果を用いる(赤色部分)。
のラプラス変換の結果を用いる(赤色部分)。
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} t^3 e^{-st} \, dt\\\\ &=& \int_0^{\infty} t^3 \left(\frac{e^{-st}}{-s}\rigth)' \, dt\\\\ &=& \left[ t^3\frac{e^{-st}}{-s}\right]_0^{\infty} +\frac{1}{s}\int_0^\infty (t^3)'\,e^{-st}\, dt\\\\ &=& \left[ t^2\frac{e^{-st}}{-s}\right]_0^{\infty} +\frac{3}{s}\textcolor{red}{\int_0^\infty t^2\cdot e^{-st}\, dt}\\\\ &=& 0+\frac{3}{s}\cdot\textcolor{red}{\frac{2}{s^3}}\\\\ &=&\frac{6}{s^3}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-066fe20f16c419609a56580d7a5496a5_l3.png)
収束: ![]()
t^n
方針:帰納法を用いる。つまり、![]() のラプラス変換の結果を用いる(赤色部分)。
のラプラス変換の結果を用いる(赤色部分)。
【証明】
![]() は上で示した。
は上で示した。![]() で下の式が成立すると仮定。
で下の式が成立すると仮定。
![]()
![]() のとき、
のとき、
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} t^n e^{-st} \, dt\\\\ &=& \int_0^{\infty} t^n \left(\frac{e^{-st}}{-s}\rigth)' \, dt\\\\ &=& \textcolor{blue}{\left[ t^n\frac{e^{-st}}{-s}\right]_0^{\infty}} +\frac{1}{s}\int_0^\infty (t^n)'\,e^{-st}\, dt\\\\ &=& \left[ t^{n-1}\frac{e^{-st}}{-s}\right]_0^{\infty} +\frac{n}{s}\textcolor{red}{\int_0^\infty t^{n-1}\cdot e^{-st}\, dt}\\\\ &=& 0+\frac{n}{s}\cdot\textcolor{red}{\frac{(n-1)!}{s^n}}\\\\ &=&\frac{n!}{s^{n+1}}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6302c62b8abbdeb4df02281724561c3a_l3.png)
収束: ![]()
※ 青色の部分における ![]() の収束は
の収束は ![]() として以下のように
として以下のように ![]() に収束することがわかる。最後の行でロピタルの定理を
に収束することがわかる。最後の行でロピタルの定理を ![]() 回用いた。
回用いた。
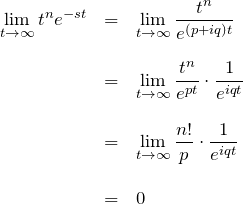
e^{s0t}
方針:普通に積分する
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} e^{s_0 t} e^{-st} \, dt\\\\ &=&\int_0^{\infty}e^{-(s - s_0)t}\, dt\\\\ &=&\left[\frac{e^{-(s - s_0)t}}{-(s-s_0)}\right]_0^{\infty}\\\\ &=&\frac{1}{s-s_0}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-46b068848266372852cb303ede5c35ca_l3.png)
収束: ![]()
※収束については ![]() と置いて、
と置いて、
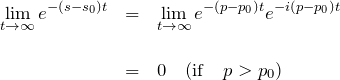
![]() であるため、収束条件は
であるため、収束条件は ![]() となる。
となる。
この結果は後の三角関数系のラプラス変換すべての土台となるため、必ず積分できるようにしておきたい。
cosωt、sinωt
方針:![]() の利用。その後でラプラス変換の実部
の利用。その後でラプラス変換の実部 ![]() と虚部
と虚部 ![]() をそれぞれ取れば良い
をそれぞれ取れば良い![]() 。これは
。これは
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Re\left[e^{i\omega t}\right]&=&\cos\omega t\\\\ \Im\left[e^{i\omega t}\right]&=&\sin\omega t\\\\ \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b1aa58c624d80ecb4a844ec59b28a436_l3.png)
![]() のラプラス変換は上の
のラプラス変換は上の ![]() において
において ![]() とすればよいが、ここでは再度
とすればよいが、ここでは再度 ![]() のラプラス変換を計算する。
のラプラス変換を計算する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} e^{i\omega t} e^{-st} \, dt\\\\ &=&\int_0^{\infty}e^{-(s - i\omega)t}\, dt\\\\ &=&\left[\frac{e^{-(s - i\omega)t}}{-(s-i\omega)}\right]_0^{\infty}\\\\ &=&\frac{1}{s-i\omega}\\\\ &=&\frac{s+i\omega}{(s-i\omega)(s+i\omega)}\\\\ &=&\frac{s+i\omega}{s^2+\omega^2}\\\\ &=&\textcolor{red}{\frac{s}{s^2+\omega^2}}+i\textcolor{blue}{\frac{\omega}{s^2+\omega^2}} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4a0bc0fe8a2458e04bab55e8e3d3abc1_l3.png)
これの両辺の実部をとれば、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Re\left[\int_0^{\infty} e^{i\omega t} e^{-st} \, dt\right] &=&\Re\left[\textcolor{red}{\frac{s}{s^2+\omega^2}}+i\textcolor{blue}{\frac{\omega}{s^2+\omega^2}}\right]\\\\ \int_0^{\infty}\Re\left[e^{i\omega t}\right]e^{-st} \, dt\right]&=& \textcolor{red}{\frac{s}{s^2+\omega^2}}\\\\ \int_0^{\infty}\cos\omega t \, dt&=&\frac{s}{s^2+\omega^2}\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ede93465cd51c4ee3120b4361e90aa72_l3.png)
また、虚部を取ると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Im\left[\int_0^{\infty} e^{i\omega t} e^{-st} \, dt\right] &=&\Im\left[\textcolor{red}{\frac{s}{s^2+\omega^2}}+i\textcolor{blue}{\frac{\omega}{s^2+\omega^2}}\right]\\\\ \int_0^{\infty}\Re\left[e^{i\omega t}\right]e^{-st} \, dt\right]&=& \textcolor{blue}{\frac{\omega}{s^2+\omega^2}}\\\\ \int_0^{\infty}\sin\omega t \, dt&=&\frac{\omega}{s^2+\omega^2}\quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-cdd6c4f65a6420a7d3e3bbe838b3b5b9_l3.png)
収束: ![]()
基本的には ![]() の積分は三角関数を指数関数で表すことによって避けるのがよい。ラプラス変換に限らず、下のように変形して計算するのが楽である。
の積分は三角関数を指数関数で表すことによって避けるのがよい。ラプラス変換に限らず、下のように変形して計算するのが楽である。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \cos\omega t&=& \frac{1}{2}\left[e^{i\omega t}+e^{i\omega t}\right]\\\\ \sin\omega t&=& \frac{1}{2i}\left[e^{i\omega t}-e^{i\omega t}\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f36ce6429f4c0c2a4493bea855071afe_l3.png)
これで部分積分を2回するといった面倒な計算を省くことができる!
cosh at、sinh at
方針:![]() のラプラス変換を実行すれば良い。そのあとに、
のラプラス変換を実行すれば良い。そのあとに、
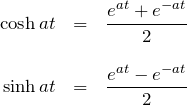
であることを使う。
![]() のラプラス変換は
のラプラス変換は ![]() の変換において、
の変換において、![]() とすればよい。したがって、
とすればよい。したがって、
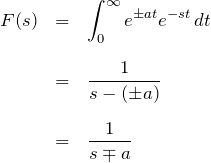
これより、
![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_0^{\infty} \cosh at \,e^{-st} \, dt&=& \int_0^{\infty} \frac{1}{2}\left[e^{at}+e^{-at}\right] e^{-st} \, dt\\\\ &=& \frac{1}{2}\int_0^{\infty} e^{at} e^{st} \, dt +\frac{1}{2}\int_0^{\infty} e^{-at} e^{-st} \, dt\\\\ &=& \frac{1}{2}\left[\frac{1}{s-a}+\frac{1}{s+a}\right]\\\\ &=& \frac{s}{s^2-a^2}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-3bdfe9dccbde1fb83ba33cb7d200ce4b_l3.png)
![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_0^{\infty} \sin at \,e^{-st} \, dt&=& \int_0^{\infty} \frac{1}{2}\left[e^{at}-e^{-at}\right] e^{-st} \, dt\\\\ &=& \frac{1}{2}\int_0^{\infty} e^{at} e^{st} \, dt -\frac{1}{2}\int_0^{\infty} e^{-at} e^{-st} \, dt\\\\ &=& \frac{1}{2}\left[\frac{1}{s-a}-\frac{1}{s+a}\right]\\\\ &=& \frac{a}{s^2-a^2}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8a62102a4c1136c087f7eee7d1159261_l3.png)
収束: ![]()
指数関数の積分はすぐに実行できるため、このあたりの結果は素早く導出できると思う。が、念のため私自身の覚え方のコツみたいなものを下に書いておく。
![]() と
と ![]() のラプラス変換の形が似ている。
のラプラス変換の形が似ている。![]() は
は ![]() で表されていたことを思い出すと、分母に
で表されていたことを思い出すと、分母に ![]() の形が現れる。分母の虚数を払った結果、「+」がでている、というイメージで覚えるのが良いと思う。
の形が現れる。分母の虚数を払った結果、「+」がでている、というイメージで覚えるのが良いと思う。
e^{at}cosωt、e^{at}sinωt
方針:![]() を指数関数で表す。つまり
を指数関数で表す。つまり
![Rendered by QuickLaTeX.com \begin{eqnarray*} e^{at}\cos\omega t &=&e^{at}\cdot\frac{1}{2}\left(e^{i\omega t}+e^{-i\omega t}\right)=\frac{1}{2}\left[e^{(a+i\omega)t}+e^{(a-i\omega)t}\right]\\\\ e^{at}\sin\omega t &=&e^{at}\cdot\frac{1}{2}\left(e^{i\omega t}-e^{-i\omega t}\right)=\frac{1}{2}\left[e^{(a+i\omega)t}-e^{(a-i\omega)t}\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-92e94aef1838ac11a185b0ca93842028_l3.png)
と、![]() のラプラス変換の結果
のラプラス変換の結果
![]()
より ![]() として求められる。
として求められる。
![]() のラプラス変換:
のラプラス変換:
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} e^{at}\cos\omega t \, e^{-st} \, dt\\\\ &=&\frac{1}{2}\int_0^{\infty}\left[e^{(a+i\omega)t}+e^{(a-i\omega)t}\right]\\\\ &=&\frac{1}{2}\left[ \frac{1}{s-(a+i\omega)}+\frac{1}{s-(a-i\omega)} \right]\\\\ &=& \frac{s-a}{(s-a)^2+\omega^2}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2746f136f52f68890908768c72ffd072_l3.png)
![]() のラプラス変換:
のラプラス変換:
![Rendered by QuickLaTeX.com \begin{eqnarray*} F(s)&=&\int_0^{\infty} e^{at}\sin\omega t \, e^{-st} \, dt\\\\ &=&\frac{1}{2}\int_0^{\infty}\left[e^{(a+i\omega)t}-e^{(a-i\omega)t}\right]\\\\ &=&\frac{1}{2}\left[ \frac{1}{s-(a+i\omega)}-\frac{1}{s-(a-i\omega)} \right]\\\\ &=& \frac{\omega}{(s-a)^2+\omega^2}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-baaf67144a5e3a65e80450bd8fa06cdc_l3.png)
収束: ![]()
別解:これは ![]() のラプラス変換
のラプラス変換 ![]() に対して、
に対して、![]() としたものに対応する(
としたものに対応する(![]() 移動)。
移動)。
2. まとめ
ラプラス変換表をまとめた。基本的には指数関数のラプラス変換さえできればおおよそ対応できる。定義さえ覚えておけばあとは積分するだけなので大した問題ではないだろう。
![]() :この方法をよく見かけるが怪しい気がする。
:この方法をよく見かけるが怪しい気がする。![]() が複素数でないといけない。
が複素数でないといけない。
cosωt、sinωtのところ
F(s)を計算している途中式の有理化で掛けているのは
s+iωなのですね
その通りです。omegaのスペルミスでωが消えていたので、修正いたしました。
ご指摘ありがとうございます。
一番最初の変換表のsinhとcoshが逆だと思います。
確認お願いします
ご指摘ありがとうございます。
表が逆になっていたようです。
e^at sinwtとe^atcoswtの方針のところの1式2式の中間のiwtに符号ついてないのが気になっちゃいました。
ご指摘感謝いたします。
修正いたしました。
sinωtの変換のところで、「また、虚部を取ると」以下で左辺がcosωtになってます。
ありがとうございます。修正いたしました。
証明まとめの1の第2式 stでtが含まれています。
また、第3式では符号が誤っています。
ありがとうございます。修正いたしました。