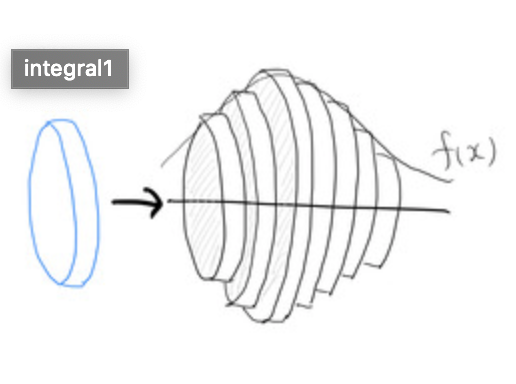
高校数学で使うのは禁忌とされている(?)パップスギュルダンの定理を用いて、トーラス(穴1個のドーナツ)の体積・表面積を求めよう。証明は省略する。ここでは、以下の例題を使って計算する。簡単な曲線の回転体なので体積・表面積は容易に計算できるはずであるが、ここでは4世紀に活躍した大先輩のアレキサンドリアのパップスを尊重したい。
中心(0,4)、半径2の円を ![]() 軸まわりに回転させた時にできる回転体の体積と表面積を求めよ。
軸まわりに回転させた時にできる回転体の体積と表面積を求めよ。
1. 体積
例題の円の方程式は、![]() である。これは2つの曲線で表すことができる。
である。これは2つの曲線で表すことができる。
![]()
であり、![]() 軸周りに回転するときの積分区間は [-2, 2] である。求めるトーラス(ドーナツ)の体積
軸周りに回転するときの積分区間は [-2, 2] である。求めるトーラス(ドーナツ)の体積 ![]() は
は![]() [(上の関数)
[(上の関数)![]() (下の関数)]dxで求められる。
(下の関数)]dxで求められる。
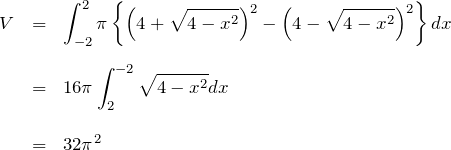
最後の式は、積分値が半径2の半円の面積 4![]() であることを用いた。パップスギュルダンの定理を用いて、結果を確認することができる。
であることを用いた。パップスギュルダンの定理を用いて、結果を確認することができる。
(回転体の体積 ![]() ) = (回転軸から図形の重心までの距離)
) = (回転軸から図形の重心までの距離) ![]() (面積
(面積 ![]() )
)
一般のトーラスの体積は、元の円の原点から中心までの距離 ![]() 、円の半径
、円の半径 ![]() とすれば、
とすれば、
![]()
で与えられる。
2. 表面積
球と同様に体積を半径で微分すると表面積になる。つまり、
![]()
いま円の中心は(0,4)で半径は2なので、![]() 、
、![]() である。よって求めるトーラスの表面積
である。よって求めるトーラスの表面積 ![]() は、
は、
![]()
となる。 パップス=ギュルダンの定理を用いても計算できる。
(回転体の体積 ![]() ) = (回転により図形の重心が描く軌跡の長さ)
) = (回転により図形の重心が描く軌跡の長さ) ![]() (元の曲線の周の長さ)
(元の曲線の周の長さ)
一般のトーラスの表面積は、元の円の原点から中心までの距離 ![]() 、円の半径
、円の半径 ![]() とすれば、
とすれば、
![]()
で与えられる。たしかに、トーラスの場合も ![]() となっている。
となっている。
表面積の計算も、回転体の表面積計算の式を使えば計算可能である。
3. まとめ
パップス=ギュルダンを見てきました。証明は省略します。あとで書きます。球と同じように、体積の式を半径で微分すると表面積になるのはおもしろい。
ちなみに、柔らかい数学でおなじみのトポロジー(位相幾何学)の分野ではドーナツとコーヒーカップは同じであると。形を変えて生産する。カーネル・サンダースはフランチャイズでコーヒーをドーナツに?