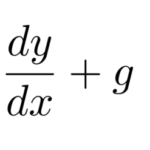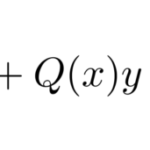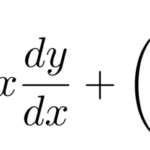ステュルム-リウヴィル(Sturm-Liouville)型微分方程式
![]()
について見ていく。2階微分方程式であるので、解には2つの積分定数が現れる。
この微分方程式を解いて一般解を求めるのではなく、物理で現れる代表的な現象がこの微分方程式に分類されることを知り、その特徴を書いた。
この微分方程式に分類されるものとして、
- 単振動を表す微分方程式
- ルジャンドルの微分方程式
- ラゲールの微分方程式
- エルミートの微分方程式
などがある。
目次
初期値問題・境界値問題
2階微分方程式であるため、解の ![]() には2つの積分定数が入ることが予想される。 したがって積分定数を確定するために、
には2つの積分定数が入ることが予想される。 したがって積分定数を確定するために、![]() あるいは
あるいは ![]() の条件を与える必要がある。
の条件を与える必要がある。
初期値問題
初期値問題では ![]() と
と ![]() を与えてやる。
ニュートンの運動方程式において、
を与えてやる。
ニュートンの運動方程式において、![]() のときの初期位置と初速度を求める問題と同じである。
このとき、与えられた初期値により微分方程式を解くことで、任意の時間
のときの初期位置と初速度を求める問題と同じである。
このとき、与えられた初期値により微分方程式を解くことで、任意の時間 ![]() の運動を決定することができる。
の運動を決定することができる。
したがって、初期値問題では与えられた ![]() と
と ![]() から、
から、![]() を得ることができる。
を得ることができる。
境界値問題
境界値問題では、![]() のある区間
のある区間 ![]() において両端の状態を与えてやる。
2つの積分定数に対する条件として、2つの以下の条件を課す。
において両端の状態を与えてやる。
2つの積分定数に対する条件として、2つの以下の条件を課す。
![]()
例として、図に挙げたような固定端や周期境界条件などがある。
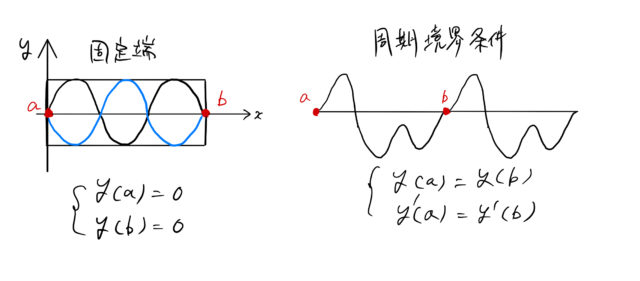
[*] あたりまえだが、固定端の条件は周期境界条件を満たしていない。
いくつかの例
具体的なものを見ていく。
単振動の微分方程式
ステュルム-リウヴィル型微分方程式において
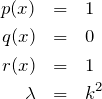
とすれば、
![]()
を得る。この解は単振動を表し、![]() の正弦波で表すことができる。 たとえば、固定端の境界条件として
の正弦波で表すことができる。 たとえば、固定端の境界条件として
![]()
の2つの条件を課すと
![]()
が成立する。したがって、微分方程式の解は ![]() の線形結合で表される。 また、
の線形結合で表される。 また、![]() となり
となり ![]() は
は ![]() による制限がある。このときの波の波長は
による制限がある。このときの波の波長は ![]() になっている。
になっている。
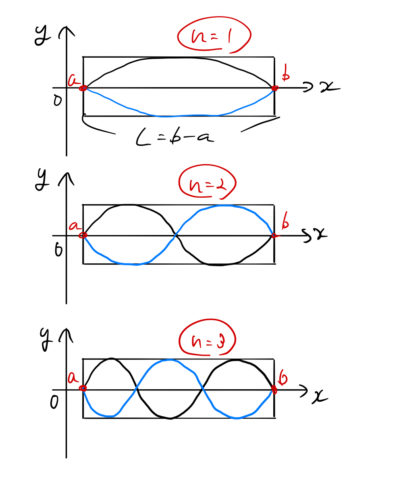
図は両端が閉じた固定端における ![]() の波を表している。 黒と青は別の時間
の波を表している。 黒と青は別の時間 ![]() での様子をあらわし、その依存性は振幅
での様子をあらわし、その依存性は振幅 ![]() となって入ってくる。
となって入ってくる。
ルジャンドルの微分方程式
ステュルム-リウヴィル型微分方程式において
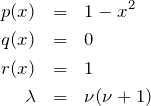
とすれば、ルジャンドルの微分方程式
![]()
が得られる。境界条件として
![]()
とすると、![]() のときに解が存在することが知られている。 その解はルジャンドル多項式
のときに解が存在することが知られている。 その解はルジャンドル多項式 ![]() によって
によって ![]() のように表される。
のように表される。
* ![]() 位のルジャンドル多項式は、
位のルジャンドル多項式は、
![Rendered by QuickLaTeX.com \begin{eqnarray*} P_l(x)\equiv y(x)&=& \sum_{k=0}^{k=\left[\frac{l}{2}\right]} (-1)^k \frac{(2l-2k)!}{2^l k! (l-k)!(l-2k)!}x^{l-2k}\\ &=& \frac{(2l)!}{2^l (l!)^2} \left\{ x^l - \frac{l(l-1)}{2(2l-1)}x^{l-2}+ \frac{l(l-1)(l-2)(l-3)}{2\cdot 4 \cdot (2l-1)(2l-3)}x^{l-4}\cdots\right\} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a44657b5c5ef12b8bac5dba19688a055_l3.png)
ここで、![]() は
は ![]() を超えない最大の整数を表す。
を超えない最大の整数を表す。
【参考】ルジャンドル多項式の導出(ルジャンドルの微分方程式を解く)
ラゲールの微分方程式
ステュルム-リウヴィル型微分方程式において
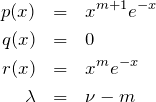
とすれば、ラゲールの陪微分方程式
![]()
を得る。
物理では波動関数の動径方向 ![]() の関数としてあらわれることが多い。 そのため、境界条件は
の関数としてあらわれることが多い。 そのため、境界条件は ![]() において多項式解をもつとする。
において多項式解をもつとする。
![]() を多項式解にする理由は、内積を求めるときの収束性にある。 たとえば、微分方程式の多項式解としてラゲール陪多項式
を多項式解にする理由は、内積を求めるときの収束性にある。 たとえば、微分方程式の多項式解としてラゲール陪多項式 ![]() が与えられるが、内積は
が与えられるが、内積は
![]()
などで与えられる(後述)。このとき![]() などが多項式解として表されていると、被積分関数が
などが多項式解として表されていると、被積分関数が ![]() の形になるため、積分の計算過程で
の形になるため、積分の計算過程で ![]() が0に収束するようになる。
が0に収束するようになる。
*ラゲールの陪多項式は、以下のような多項式展開が可能である。
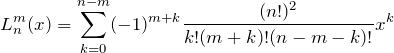
エルミートの微分方程式
ステュルム-リウヴィル型微分方程式において
とすれば、エルミートの微分方程式
![]()
を得る。
ラゲールの陪微分方程式の場合と同様に ![]() において多項式解であるという境界条件を課す。 その場合、
において多項式解であるという境界条件を課す。 その場合、 ![]() であることが知られており、解はエルミート多項式
であることが知られており、解はエルミート多項式 ![]() で表すことができる。
で表すことができる。
* エルミート多項式を多項式の形で書くと
![Rendered by QuickLaTeX.com \begin{eqnarray*} H_n(x)=\sum_{k=0}^{\left[\frac{n}{2}\right]}(-1)^k \frac{n!}{k!(n-2k)!}(2x)^{n-2k} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b7c7c63f14abbc9eebd5ed4a1a70927a_l3.png)
となる。
** 次の項で示すように、内積は
![]()
となる。
![]()
とエルミート関数 ![]() を定義すると、エルミート関数は直交する。つまり
を定義すると、エルミート関数は直交する。つまり
![]()
である。
固有値・固有値展開
行列で見られる固有値・固有関数という言葉は、微分方程式でも使われる。
固有値/固有関数
ステュルム-リウヴィル型微分方程式
![]()
における ![]() は境界条件によって決まる。 単振動の場合は、波数
は境界条件によって決まる。 単振動の場合は、波数 ![]() に関して
に関して ![]() であった。 また、ルジャンドル多項式を考えた場合は、
であった。 また、ルジャンドル多項式を考えた場合は、![]() となっていた。
となっていた。
![]() は特定の値をとることから固有値と呼ばれる。
また、その固有値に対応する解のことを固有関数と呼ぶ。
ある波数
は特定の値をとることから固有値と呼ばれる。
また、その固有値に対応する解のことを固有関数と呼ぶ。
ある波数 ![]() に対応する
に対応する ![]() が固有関数であった。
が固有関数であった。
2つの固有値 ![]() に対して、対応する固有関数
に対して、対応する固有関数 ![]() を考えたとき、 ステュルム-リウヴィル型微分方程式では
を考えたとき、 ステュルム-リウヴィル型微分方程式では
![]()
が成立する。これは異なる固有値を持った固有関数は直交することをあらわしている。
![]()
で定義する。このとき元の微分方程式は
![]()
となる。これを用いてそれぞれの固有関数
![]()
一方で左辺が
![]()
でもあるので、
![]()
となる。これの両辺を境界条件の範囲
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_a^b (\lambda_m - \lambda_n)r(x)\phi_m(x)\phi_n(x)\, dx&=& \left[\left(p(x)\left(\phi_m(x)\frac{d\phi_n(x)}{dx}-\phi_n(x)\frac{d\phi_m(x)}{dx}\right) \right)\right]_a^b\\ &=&\textcolor{red}{0} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-18041688f687df17db417144fe7c30ad_l3.png)
となる
![]()
となる。これより異なる固有値
「境界値問題」のところで説明したように、
![]()
であった。ここで、
(i)
(i)
![]()
(i)
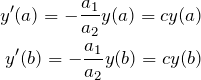
となる。これにより、境界における微分値を
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\left[\left(p(x)\left(\textcolor{red}{\phi_m(x)}\frac{d\phi_n(x)}{dx}-\textcolor{red}{\phi_n(x)}\frac{d\phi_m(x)}{dx}\right) \right)\right]_a^b\\ &=&\quad p(b)\Bigl( \phi_m(b)\phi_n'(b) -\phi_n(b)\phi_m'(b) \Bigr)\\ &-&\quad p(a)\Bigl( \phi_m(a)\phi_n'(a) -\phi_n(a)\phi_m'(a) \Bigr)\\ &=&\quad p(b)\Bigl( \phi_m(b)\cdot c\phi_n(b) -\phi_n(b) \cdot c\phi_m(b) \Bigr)\\ &-&\quad p(a)\Bigl( \phi_m(a)\cdot c\phi_n'(a) -\phi_n(a)\cdot c\phi_m(a) \Bigr)\\ &=&0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e7c432ce7acf784f6d2b6265f52aec18_l3.png)
となる。
上記で見てきた4つの場合についてみていく。 それぞれの ![]() の値を具体的に代入して、上で見た
の値を具体的に代入して、上で見た ![]() の境界条件を与えた場合、解となっている固有関数(エルミート多項式
の境界条件を与えた場合、解となっている固有関数(エルミート多項式![]() など)について見てみると
など)について見てみると
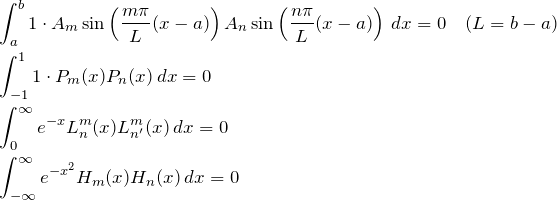
となる。式は上から、単振動(固定端)、ルジャンドルの微分方程式、ラゲールの陪微分方程式、エルミートの微分方程式である。 単振動については三角関数の直行性から容易に証明できる。それ以外についての証明はここではおこなわないが、よく知られている結果である。
内積と正規直交基底
![]() の直交性を利用して、正規直交基底をつくる。
の直交性を利用して、正規直交基底をつくる。
そこで関数空間で内積を
![]()
で定義すると、![]() を規格化できる。関数を、関数のノルム(大きさ)で割れば良い。
を規格化できる。関数を、関数のノルム(大きさ)で割れば良い。
![]()
![]() の直交性から、規格化された固有関数
の直交性から、規格化された固有関数 ![]() は正規直交基底をつくることができる。 4つの例における正規直交基底を示す。
は正規直交基底をつくることができる。 4つの例における正規直交基底を示す。
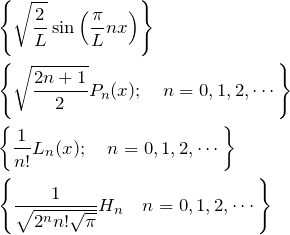
このような正規直交基底を用いて、関数を展開することは多い。
また、単振動の微分方程式を周期境界条件で解くと、
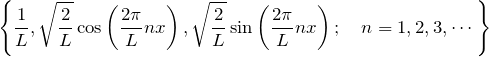
となる。この正規直交基底によって、関数が展開される場合がフーリエ級数展開である。