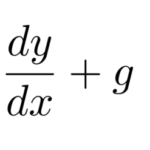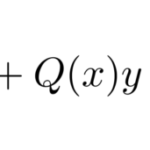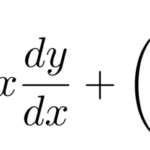ルジャンドル多項式
![]()
は、ルジャンドルの微分方程式の2つ特殊解から作られる。 ルジャンドルの微分方程式は2階線形微分方程式で、
![]()
で与えられる。 そのことを詳しく見ていき、ルジャンドル多項式を導出する。 ここでは物理の話は一切なく、黙々と多項式を導出する。
0. ルジャンドルの微分方程式の特殊解
計算の詳細は「ルジャンドルの微分方程式/級数解による解法」に書いた。ここでは簡単に結果だけまとめておこう。
ルジャンドルの微分方程式は
![]()
で与えられる2階線形微分方程式である。
![]() まわりの級数解
まわりの級数解
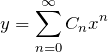
と置いて、微分方程式へ代入する。
そうすると ![]() の漸化式
の漸化式
![]()
が得られる。この漸化式は1個おきの係数の関係を表しているため、![]() の任意性がある。
の任意性がある。
- (i)
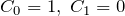
- (ii)
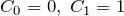
の2つの場合を考えて、級数解を求めることができる。
つまり、(i)に対する特殊解 ![]() と (ii)に対する特殊解
と (ii)に対する特殊解 ![]() を得る。
を得る。
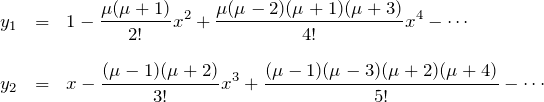
また、ルジャンドルの微分方程式の一般解は上記の2つの特殊解の線型結合で表すことができる![]() 。
。
![]()
ここで、![]() は定数である。
は定数である。
1. ルジャンドル多項式の導出
上のルジャンドルの微分方程式の2つの特殊解からルジャンドル多項式を導出していく。
2つの特殊解の係数Cnの特徴
2つの特殊解は
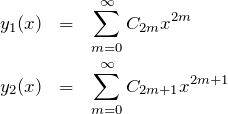
の形をしている。 これらの展開係数 ![]() の特徴をまとめておこう。
の特徴をまとめておこう。
1つの特殊解 ![]() に対して:
に対して:
![]()
である。ただし、![]() である。
である。
漸化式の形から、![]() があるところで0であるなら、それ以降の項は0である。たとえば、
があるところで0であるなら、それ以降の項は0である。たとえば、![]() とすれば、漸化式より
とすれば、漸化式より ![]() となる。ドミノ倒しが途中で終了してしまう様子に似ている。重要なのは「どのような場合にどの項が0になるか」である。
となる。ドミノ倒しが途中で終了してしまう様子に似ている。重要なのは「どのような場合にどの項が0になるか」である。
つまり、上の係数(1)の分子が0になる場合を調べる。たとえば、![]() のとき、
のとき、![]() であるが、
であるが、
![]()
となり、![]() となる。したがって、
となる。したがって、![]() のときの特殊解
のときの特殊解 ![]() は
は
![]()
となる。
次に ![]() のときを考える。
のときを考える。
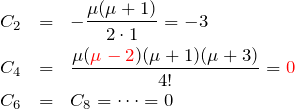
となる。よって、特殊解は
![]()
となる。
次に ![]() のときも考えておこう。
のときも考えておこう。
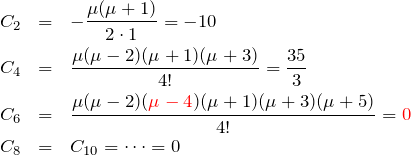
となる。よって、特殊解は
![]()
となる。
以上より、![]() が0以上の偶数のとき、特殊解
が0以上の偶数のとき、特殊解 ![]() は
は ![]() 次の多項式となる。
次の多項式となる。
もう1つの特殊解 ![]() に対して:
に対して:
こちらも同様に計算できる。係数は
![]()
であった。ここで、![]() である。
である。
![]() のとき:
のとき:
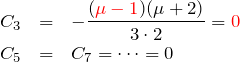
となる。よって、特殊解は
![]()
となる。
次に ![]() のとき:
のとき:
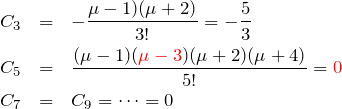
となる。よって、特殊解は
![]()
となる。
同様にして ![]() のときの特殊解
のときの特殊解
![]()
となる。
以上より、![]() が正の奇数のとき、特殊解
が正の奇数のとき、特殊解 ![]() は
は ![]() 次の多項式となる。
次の多項式となる。
0以上の整数μに対する2つ特殊解
以上の結果をまとめておく。
| | 特殊解の形(多項式) |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| … | … |
この表から分かる通り、0以上の整数 ![]() に対して表の右の多項式を対応させることができる。 つまり、
に対して表の右の多項式を対応させることができる。 つまり、![]() を決めれば多項式の形が決まる。
を決めれば多項式の形が決まる。
また、この多項式はもともとのルジャンドルの微分方程式の特殊解であった。 したがって ![]() を定数倍したものも、また微分方程式の解となる(一般解の形が
を定数倍したものも、また微分方程式の解となる(一般解の形が ![]() であるため)。
であるため)。
ルジャンドル多項式 ![]() は、
は、![]() のときに多項式の値が1になるように
のときに多項式の値が1になるように ![]() (
(![]() )を定数倍したもので定義される。つまり、上記の表の多項式をそれぞれ
)を定数倍したもので定義される。つまり、上記の表の多項式をそれぞれ ![]() (
(![]() )の値で割ったものがルジャンドル多項式である。
)の値で割ったものがルジャンドル多項式である。
![]() の値を決めればルジャンドル多項式の形が決まる。つまり、
の値を決めればルジャンドル多項式の形が決まる。つまり、![]() を満たす条件のもと、上の表と同じようなものができる。
を満たす条件のもと、上の表と同じようなものができる。
| | ルジャンドル多項式 |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| … | … |
再度説明すると、もともとがルジャンドル多項式は、ルジャンドルの微分方程式を満たす特殊解の定数倍で作られた。したがって、上のルジャンドル多項式は対応する ![]() の値に対するルジャンドルの微分方程式を満たす解である。
の値に対するルジャンドルの微分方程式を満たす解である。
ルジャンドル多項式の形
ルジャンドル多項式のはじめの項を少し変形してみよう。
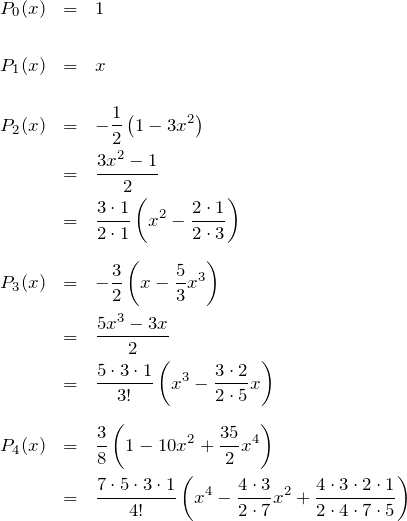
これより、一般的なルジャンドル多項式の形がわかる。
![]()
![]() 次の多項式になる。
次の多項式になる。
2. まとめ
ルジャンドル多項式の導出をおこなった。時々 物理学で出てくるが、忘れたら覚えなおせば良い。
夏休みの宿題で、「ルジャンドル多項式の導出」や「ルジャンドル多項式で読書感想文」などが出たときに再度このページで学んでもらいたいと思う。