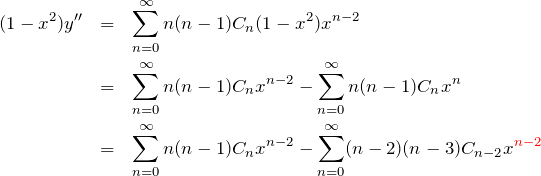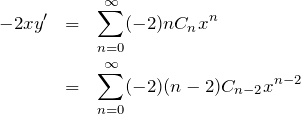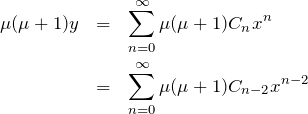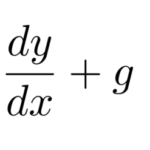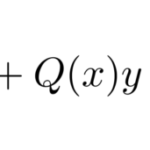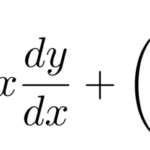ルジャンドルの微分方程式
![]()
を解いて2つの特殊解を求める。微分方程式は ![]() まわりの級数展開により解いていく。「【微分方程式】級数解による解法(整級数)」の手法がそのまま使える。
まわりの級数展開により解いていく。「【微分方程式】級数解による解法(整級数)」の手法がそのまま使える。
得られる2つの特殊解は「ルジャンドル多項式の導出」と深い関係がある。
1. ルジャンドルの微分方程式の解法
級数解を置く前に微分方程式の形をみておこう。 ルジャンドル多項式は以下の形をとる。
![]()
変形すると
![]()
となる。この2階線形微分方程式は ![]() で確定特異点をもつ。 確定特異点まわりで級数展開するのが常だが、ここでは一般解を
で確定特異点をもつ。 確定特異点まわりで級数展開するのが常だが、ここでは一般解を ![]() まわりの正則点(特異点でない)ところで展開していく。
まわりの正則点(特異点でない)ところで展開していく。
* 確定特異点については「 微分方程式】確定特異点と級数の置き方/計算のコツ」にまとめた。級数解の計算テクニックなども載せているので参考にされたい。
** [難] ルジャンドルの微分方程式は変数変換により、超幾何微分方程式(ガウスの微分方程式)に変換できる。変数変換は確定特異点である ![]() を原点にシフトする変換である。超幾何微分方程式に変換できるため、ルジャンドルの微分方程式の
を原点にシフトする変換である。超幾何微分方程式に変換できるため、ルジャンドルの微分方程式の ![]() における特殊解は超幾何関数
における特殊解は超幾何関数 ![]() により表すことができる。
により表すことができる。
級数解を置いて微分方程式へ代入
![]() まわりの級数を
まわりの級数を
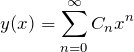
と置く。このように置くことで、微分方程式の一般解を求める問題を ![]() を求める問題に帰着させることができる。
を求める問題に帰着させることができる。
微分する:
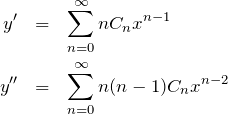
これらを微分方程式(1) へ代入する。
微分方程式へ代入した時の ![]() の係数は
の係数は
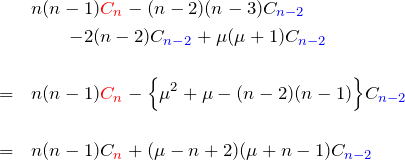
これを0と置いて
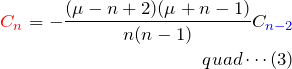
を得る。これは級数解の係数に関する漸化式である。
2つの特殊解と一般解
特殊解を求めるときは、![]() を任意に取れる
を任意に取れる ![]() 。 以下では、
。 以下では、
- (i)
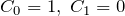
- (ii)
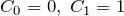
の場合を考える。
(i) ![]() のとき:
のとき:
漸化式(3)より
![]()
また
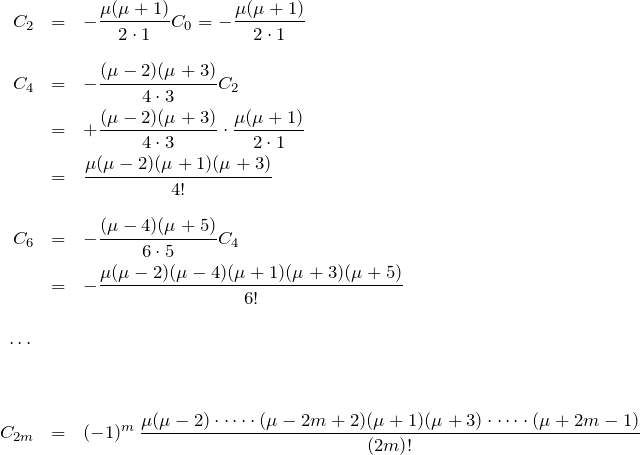
よって特殊解は
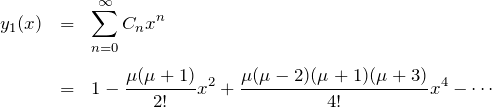
(ii) ![]() のとき:
のとき:
漸化式(3)より
![]()
また
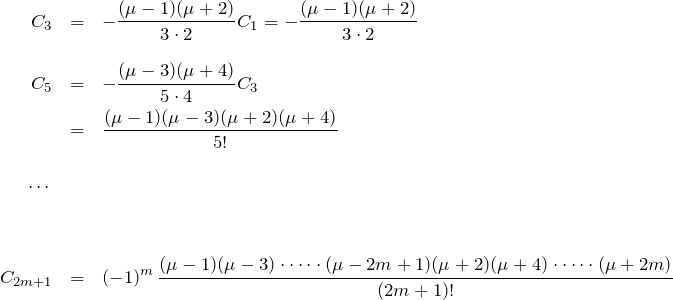
よって特殊解は
![]()
一般解: ルジャンドルの微分方程式の一般解は上記の2つの特殊解の線型結合で表すことができる![]() 。 よって一般解:は
。 よって一般解:は
![]()
ここで、![]() は定数で、
は定数で、
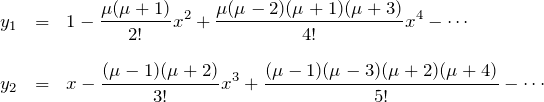
である。
ここで得られた特殊解の形は多項式の形をしている。![]() によって多項式の形が変わることもわかる。
によって多項式の形が変わることもわかる。![]() は「ルジャンドル多項式」と関係する。
は「ルジャンドル多項式」と関係する。
* C0,C1を任意にとれる意味(特殊解の意味)
ここでの「特殊解」は、2階線形微分方程式の一般解の定数 ![]() がある値のときの解に対応する。上記で任意に
がある値のときの解に対応する。上記で任意に ![]() を決めて、(i)(ii)と場合分けしたそれぞれの特殊解は一般解において
を決めて、(i)(ii)と場合分けしたそれぞれの特殊解は一般解において
- (i)
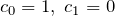
- (ii)
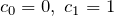
とした場合と同じである。
2階線形の微分方程式は
![]()
のように2つの特殊解 ![]() の線型結合で表されているのであったから、特殊解
の線型結合で表されているのであったから、特殊解 ![]() を見つければよかったのである。定数倍異なる
を見つければよかったのである。定数倍異なる ![]() を見つけても一般解の形には影響しないため、任意に
を見つけても一般解の形には影響しないため、任意に ![]() を決めてよかった。
を決めてよかった。
ただし、注意しなければならないのは2つの特殊解が線型独立であるということを調べないといけない。したがって、2つの特殊解を ![]() として独立でないものを選ぶのは無意味である。今回の場合は
として独立でないものを選ぶのは無意味である。今回の場合は ![]() が
が ![]() の多項式であり、
の多項式であり、![]() が
が ![]() の多項式であるため、線型独立である。
の多項式であるため、線型独立である。
* 解が線形独立かどうか調べるためにはロンスキアン ![]() を計算すると良い。
を計算すると良い。
![]()
であれば ![]() は線型独立である。
は線型独立である。
2. まとめ
ルジャンドルの微分方程式を解いてきた。級数解を用いて微分方程式を解く手法の例題としてよいと思う。また、級数解の解法における「特殊解」の意味をおさえておきたい。一般解の形からある特定の解が特殊解なのである。
余程のことがない限りルジャンドルの微分方程式は覚える必要はない。物理の教科書で出てきたときは、その都度、調べて思い出せば良いだろう。