確定特異点のある微分方程式を級数解で解く。 ここでは特異点とは何かを説明し、解法をみていく。それを用いて後で例題を解いていく。 例題として、確定特異点のある微分方程式は以下のようなものである(![]() が確定特異点)。
が確定特異点)。
![]()
目次
1. 確定特異点のある微分方程式
ここでは線形型
![]()
の微分方程式について見ていく。例題も ![]() の形に変形すればこの線形型になる。
の形に変形すればこの線形型になる。
特異点と確定特異点
![]()
を変形しよう
![]()
となる。したがって
![]()
とすれば、![]() の線形型微分方程式となる。 これより、
の線形型微分方程式となる。 これより、![]() は
は ![]() のそれぞれの特異点である。 また、
のそれぞれの特異点である。 また、![]() は式(1)の確定特異点である。
は式(1)の確定特異点である。
用語をざっくりまとめておこう。
特異点
![]() が特異点であるとは、ある多項式
が特異点であるとは、ある多項式 ![]() に対して
に対して ![]() で
で ![]() がバグること。 ここでは
がバグること。 ここでは ![]() に対して、
に対して、![]() はともにバグる。
はともにバグる。
正則点
![]() が正則点であるとは、ある多項式
が正則点であるとは、ある多項式 ![]() に対して
に対して ![]() で
で ![]() がバグらないこと。 つまり、特異点でない点のこと。
がバグらないこと。 つまり、特異点でない点のこと。
確定特異点
![]() が確定特異点であるとは、
が確定特異点であるとは、![]() の両方が
の両方が ![]() で正則ではない点のこと。このとき、
で正則ではない点のこと。このとき、![]() を微分方程式の確定特異点と呼ぶ。
を微分方程式の確定特異点と呼ぶ。
![]() が特異点か正則点か4通りある。確定特異点は少なくとも一方が特異点のときである。
が特異点か正則点か4通りある。確定特異点は少なくとも一方が特異点のときである。
| ( | ||
| 確定特異点である | 確定特異点である | |
| 確定特異点である | 確定特異点ではない |
確定特異点ではない場合は正則点まわりで展開すれば良い。確定特異点がある場合は、以下のような級数解の形を仮定して解いていく。
級数解の置き方
![]() が確定特異点のときは下のように級数解を置く。
が確定特異点のときは下のように級数解を置く。
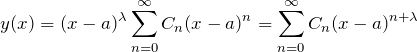
特異点周りの冪(![]() のn乗の形)で展開している。
のn乗の形)で展開している。
例題では ![]() が式(1)の確定特異点になっているため、
が式(1)の確定特異点になっているため、
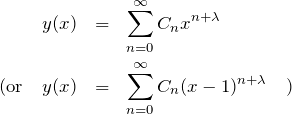
と置く。上の方が簡単な式なので上を用いるのが良いが、下の方でも解くことができる。
微分方程式の解 ![]() を求めるという最終的な目標のためには、
を求めるという最終的な目標のためには、
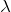 を求める
を求める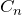 を求める
を求める
ことが必要である。![]() と
と ![]() を決定するためには、上の
を決定するためには、上の ![]() を1階、2階微分したものを元の微分方程式へ代入する。
を1階、2階微分したものを元の微分方程式へ代入する。
級数解の1階微分、2階微分
例題の微分方程式に対して、級数解の形を
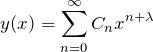
と置くと、1階、2階微分は
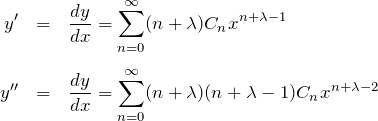
となる。これを微分方程式へ代入していき、![]() を求めていく(計算詳細は例題の解答)。
を求めていく(計算詳細は例題の解答)。
* ![]() が満たすべき式を決定方程式と呼ぶ。名前は覚えなくてよいかもしれない。
が満たすべき式を決定方程式と呼ぶ。名前は覚えなくてよいかもしれない。
解法まとめ
確定特異点を持つ微分方程式の級数解による解法を示す。
- 確定特異点を探す(
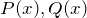 の特異点を調べる)
の特異点を調べる) - 級数解を確定特異点周りで展開した以下の形にする
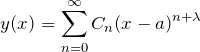
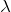 を求める
を求める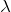 に対して
に対して 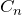 を求める
を求める
2. 計算のコツ
よく計算に使うものをまとめておく。
TIPS①: Σの添字ずらし
![]() の形からわかるように、
の形からわかるように、![]() で表された級数をもとの微分方程式に代入すると、
で表された級数をもとの微分方程式に代入すると、![]() がついた方程式が得られる。それを
がついた方程式が得られる。それを
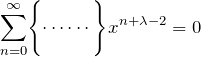
のような形にしたい。なぜなら、この形にすると任意の ![]() に対してこの方程式が成り立つため、
に対してこの方程式が成り立つため、![]() 内を
内を ![]() とできるからである。そして得られた関係式より、
とできるからである。そして得られた関係式より、![]() を求めることができる。
を求めることができる。
やってみるとわかるが、問題は普通に![]() を代入してもうまく
を代入してもうまく ![]() にまとめられないことである。というのも
にまとめられないことである。というのも
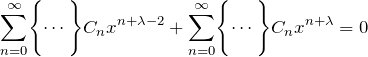
のような形になるからである。綺麗にまとめられない問題は、見ての通り ![]() の指数が異なっているためである。
の指数が異なっているためである。
2項目の ![]() を 1行目の
を 1行目の ![]() に揃えたい。そのために、以下のように
に揃えたい。そのために、以下のように ![]() の取り方を変える。
の取り方を変える。
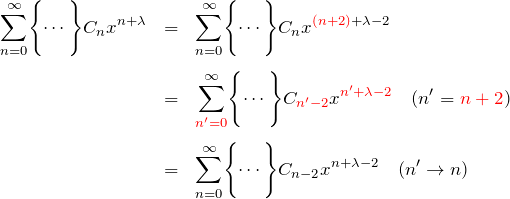
この問題の鍵は、左辺を最後の行に変形できるかどうかである。 このようにして ![]() に揃えることができる。
に揃えることができる。
この変形で気になるのは次の点であろう。
TIPS②: nが負の展開係数の定義
上の式の最後は ![]() が
が ![]() 始まっている。 したがって、展開係数は
始まっている。 したがって、展開係数は ![]() となる。このことは不都合に見えるかもしれない。
となる。このことは不都合に見えるかもしれない。
しかし、負の添え字を持つ展開係数 ![]() は
は ![]() と定義してしまえば良い。このように定義すれば、
と定義してしまえば良い。このように定義すれば、![]() だとしても実質的には
だとしても実質的には ![]() と同じように扱える。
と同じように扱える。
つまり上の式では ![]() から始めるのと同じである。
から始めるのと同じである。
3. 例題の解答
以下、TIPS(1), TIPS(2)が出てくるところは示してる。
確定特異点を調べる
![]()
を変形して
![]()
となる。したがって
![]()
となる。![]() はそれぞれ
はそれぞれ ![]() の特異点である。したがって、
の特異点である。したがって、![]() は微分方程式(1)の確定特異点である。
は微分方程式(1)の確定特異点である。
級数とその微分
![]() の確定特異点に対して、級数を
の確定特異点に対して、級数を
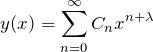
と置く。このとき、
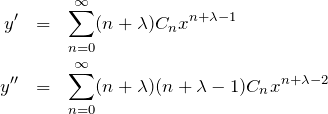
である。これを微分方程式(1)へ代入していく。項を3つ分けて計算していく。
第1項 (![]() の項):
の項):
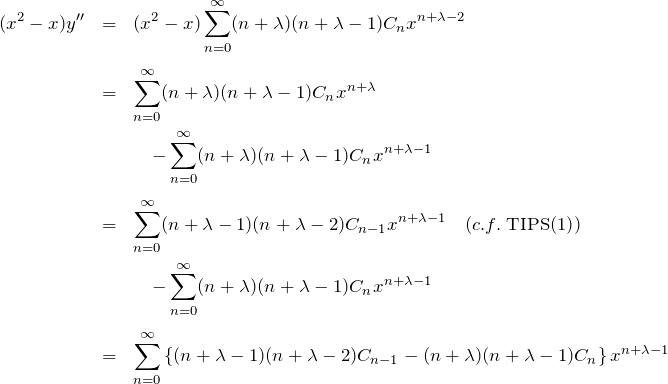
第2項 (![]() の項):
の項):
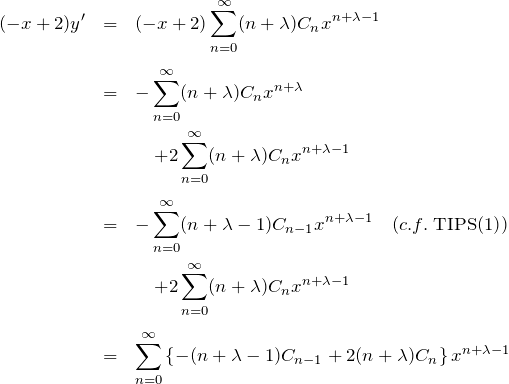
第3項 (![]() の項):
の項):
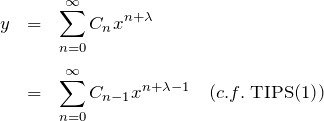
これらを微分方程式(1)へ代入してまとめる。
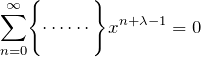
ここで以下の ![]() の部分は任意の
の部分は任意の ![]() に対して0である。
に対して0である。
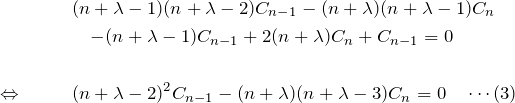
この変形は ![]() の形に注目して展開すればできる。この式(3)は
の形に注目して展開すればできる。この式(3)は ![]() を決定する「決定方程式」と呼ぶ。
を決定する「決定方程式」と呼ぶ。
λを求める、Cnを求める
![]() のとき、式(3)は
のとき、式(3)は
![]()
ここで、![]() より、
より、
![]()
![]() より
より ![]() である。
である。
(i) ![]() のとき:
(3)より
のとき:
(3)より
![]()
である。これは ![]() に関する漸化式で、
に関する漸化式で、![]() を決定できる。何個か調べていく。
を決定できる。何個か調べていく。
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]() は決まらない。
は決まらない。
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]()
![]() 以降についても同様に求められる。
以降についても同様に求められる。
上の結果から、
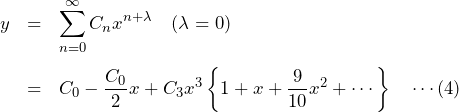
となる。ここで、![]() は定数である。
は定数である。
(i) ![]() のとき:
(3)より
のとき:
(3)より
![]()
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]()
![]() 以降も同様に求めることができる。
以降も同様に求めることができる。
これより、
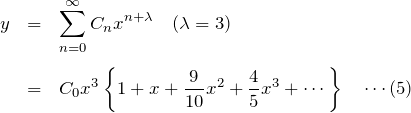
(式(5)における ![]() と式(4)の
と式(4)の![]() は別もの)。
は別もの)。
式(4)(5)の級数解の結果を合わせて
![]()
(![]() は定数である。)
は定数である。)
* もともとの微分方程式が2階の線形微分方程式であったため、線形独立な2つの解が得られている。それぞれ独立な解を ![]() で線型結合したものが一般解となる。
で線型結合したものが一般解となる。![]() に関しては、2階の線形なので2つの
に関しては、2階の線形なので2つの ![]() が得られ、それぞれの
が得られ、それぞれの ![]() に対してそれぞれ級数解が得られる。そのうち線形独立なものは2つであるため、(4)と(5)で共通する
に対してそれぞれ級数解が得られる。そのうち線形独立なものは2つであるため、(4)と(5)で共通する
![]()
が現れたのは偶然ではない。
4. まとめ
確定特異点の求め方から、級数解の求め方を扱った。級数解を用いて微分方程式を解こうとすると計算量が多くなる傾向にあると思う。がんばって計算してほしい。
計算のコツはここでの例題だけでなく、いくつかの ![]() 計算で使えるので覚えておくと良い。
計算で使えるので覚えておくと良い。
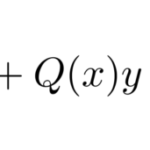
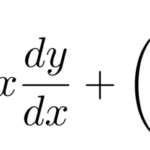
(4)の式の2項目にxがぬけているのではないでしょうか?
ちょうどこの問題でつまずいていたのでとても参考になりました。ありがとうございます。
横国大院の過去問なんですね
すみません、修正いたしました。ありがとうございます。
過去問とは知らなかったです。とにかくお役に立てて良かったです。