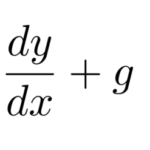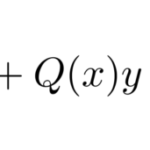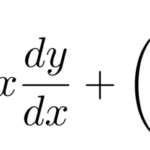微分方程式を級数解によって解くとは、微分方程式の解の形を
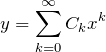
などと置いてしまって展開係数 ![]() を求める問題に替えて解くことである。例題を見ていこう。
を求める問題に替えて解くことである。例題を見ていこう。
以下の微分方程式を級数を用いて解け。
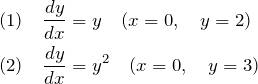
1. 級数解による解法
例題は変数分離型なので簡単に解けるが、ここでは級数解による解法の練習として解いていこう。
級数解で解く必要性
与えられた微分方程式の解が ![]() の形であるならば、級数解で求めたものは
の形であるならば、級数解で求めたものは ![]() のテイラー展開の形になっているだろう。
のテイラー展開の形になっているだろう。
![]()
もっと複雑な ![]() などになっている場合だってある。 この解を求めるために、複雑な微分方程式を「同時型だ」「変数分離だ」とするよりも、あらかじめ解の形を決めておいて展開係数を求めるほうが簡単になる場合もある。
などになっている場合だってある。 この解を求めるために、複雑な微分方程式を「同時型だ」「変数分離だ」とするよりも、あらかじめ解の形を決めておいて展開係数を求めるほうが簡単になる場合もある。
そもそも微分方程式の解が多項式になる場合だってある。 その場合に真面目に微分方程式を解くのではなく、級数解を求めるほうがずっと楽である。
微分方程式の解を ![]() などの形で求めるのではなく、
などの形で求めるのではなく、![]() などと置いて展開係数を求める問題にすり替える。
などと置いて展開係数を求める問題にすり替える。
どのように級数展開するか?
当面の問題はどのように展開するかである。
級数解によって微分方程式を解く場合には初期条件が与えられている(または自分で見つける)。初期条件は 「![]() のとき
のとき ![]() 」の形になっている。これは1つの条件が与えられているということを意味する。
」の形になっている。これは1つの条件が与えられているということを意味する。
1つの条件があるため、うまい形に展開形を書いておけば展開係数のうち1つを与えることができる。
適当な形で![]() を展開すれば、
を展開すれば、
1つの初期条件 → 1つの展開係数
とできる。 適当な条件とは何だろうか?例えば条件が 「![]() のとき
のとき ![]() 」の場合は
」の場合は
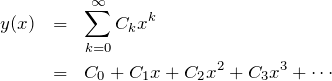
とおけば良い。その理由は ![]() を代入するとわかる。
を代入するとわかる。
![]()
このように1つの初期条件から1つの展開係数を求めることができる。
しかし、この展開は 「![]() のとき
のとき ![]() 」の条件では綺麗に解けない。
」の条件では綺麗に解けない。![]() を代入すると
を代入すると
![]()
となる。展開係数に関する条件は得られるものの、展開係数が求められたわけではない。
一般に整級数で展開する場合、「![]() のとき
のとき ![]() 」の条件に対して
」の条件に対して
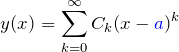
と展開する。このとき、![]() と展開係数が1つわかる。
と展開係数が1つわかる。
展開係数C0がわかったとて
本来の目的は ![]() を含めてすべての展開係数を求めることである。 そのためには、展開した形をもともとの微分方程式に代入する必要がある。
を含めてすべての展開係数を求めることである。 そのためには、展開した形をもともとの微分方程式に代入する必要がある。
例題で見るように、展開形を微分方程式に代入すると、展開係数同士の関係が得られる。 いま ![]() がわかっているため、
がわかっているため、![]() と順番に求められることも多い。 また、
と順番に求められることも多い。 また、![]() の形の規則性を見極める力もいる。
の形の規則性を見極める力もいる。
このことは具体的な例題をみて押さえておこう。
解法まとめ
- 微分方程式を整級数で展開
(初期条件が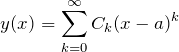
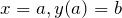 の場合)
の場合)
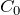 を求め、展開係数間の関係が漸化式になっている場合は、
を求め、展開係数間の関係が漸化式になっている場合は、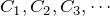 と順番に求めていく
と順番に求めていく
2. 例題の解答
![]() によって初期条件が与えられているので展開は
によって初期条件が与えられているので展開は
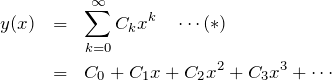
とする。
例題(1)の解答
![]()
左辺を求める:
(*)を微分して
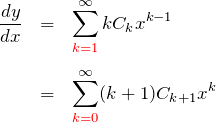
- 定数
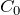 を微分すると0、つまり
を微分すると0、つまり 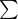 は
は 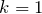 から始める
から始める - 右辺と比較するため、
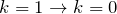 に直しておく
に直しておく
右辺はそのまま ![]() なので微分方程式は
なので微分方程式は
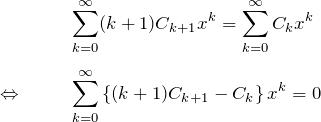
この式が任意の ![]() について成立するため、
について成立するため、
![]()
となる。これは ![]() と
と ![]() を結ぶ漸化式である。初項である
を結ぶ漸化式である。初項である ![]() は初期条件より
は初期条件より
![]()
となる。
展開係数を求める:
上の漸化式(1)の一般項は簡単に求めることができる。(1)を繰り返して用いると
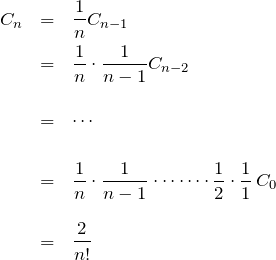
となる。
以上より、級数解は
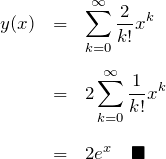
となる。これが微分方程式の解である。
*最後の行で ![]() のマクローリン展開(
のマクローリン展開(![]() まわりのテイラー展開)を用いた。
まわりのテイラー展開)を用いた。
![]()
例題(2)の解答
![]()
![]() を求める:
を求める:
初期条件より ![]() となる。
となる。
左辺を求める:
例題(1)と同様に(*)を微分して
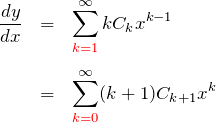
である。
右辺を求める:
![]() を計算し、
を計算し、![]() の降べきの順に並べる
の降べきの順に並べる
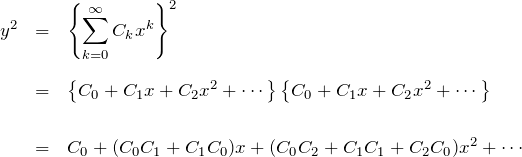
![]() であるが、後の説明のため分けて書いた。
ここで、
であるが、後の説明のため分けて書いた。
ここで、![]() の係数は
の係数は
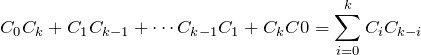
である。
展開係数を求める:
![]() の係数を左辺と右辺でまとめておこう。
の係数を左辺と右辺でまとめておこう。
| 左辺 | 右辺 | |
| … | … | … |
| … | … | … |
![]() の係数を比較して
の係数を比較して
![]()
![]() の係数を比較して
の係数を比較して
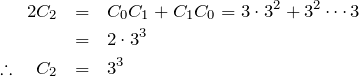
![]() の係数を比較して
の係数を比較して
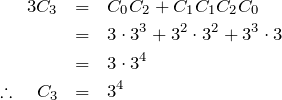
これより、
![]()
と推測できる。これを帰納法によって証明する。
【帰納法】
(i) ![]() のときは、
のときは、![]() より成立。
より成立。
(ii) ![]() のとき
のとき ![]() と仮定
と仮定
![]() の係数について
の係数について
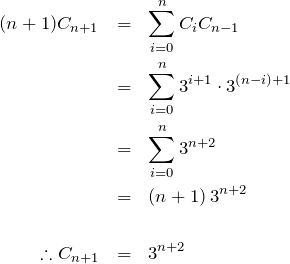
したがって、![]() のときも成立する。
のときも成立する。![]()
【帰納法おわり】
以上より級数解は
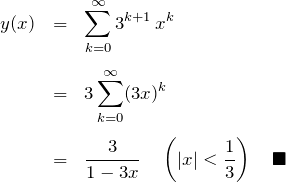
*最後の行は、無限等比級数を簡単にした形を用いている。収束条件があることに注意する。
3. まとめ
級数解の基本的な解き方を見てきた。適当な展開形を仮定することで、展開係数を求める問題に帰着させることができた。また、展開係数は数列になっているため簡単に求めることができた。
この級数解による解法はいくつかの基本的な問題に対しても解くことができる。簡単な微分方程式を級数解で解くのも良い訓練になる。