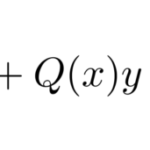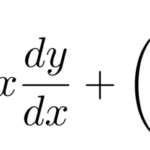クレローの微分方程式は
![]()
の形をしている。 ここではその解き方をまとめて、以下の例題を解けるようにする。包絡線と関係するので、そのことも簡単にまとめる。 よくわからないけど今すぐ解きたいというのなら、「解法まとめ」だけ参考にしたら良い。
以下のクレローの微分方程式を解け。ただし、![]() である。
である。
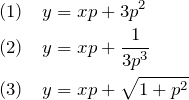
1. クレローの微分方程式とは
一般的な話をして、解き方をまとめる。
微分方程式の形
冒頭に示したように、クレローの微分方程式の形は
![]()
である。以下では ![]() と置いて
と置いて
![]()
と書く。この微分方程式には以下に示すように一般解と特異解がある。式(*)は後で何回も使う式であるため大事にしておく。
一般解と特異解を求める
一般解と特異解を求めよう。 ここでいう微分方程式の一般解と特異解はざっくりと以下の通りである。
- 一般解:定数
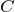 によって表される式
によって表される式 - 特異解:一般解で表されていない式(
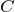 を含まない)
を含まない)
これらを求めるために、微分方程式(*)の両辺を ![]() で微分してみよう。
で微分してみよう。
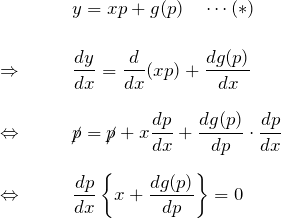
これは、
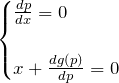
を表す。以下で示すように、上の式から一般解が求められ、下の式から特異解が求められる。
まず、一般解を見ていこう。 上の方の簡単な微分方程式の解は、![]() である。
である。![]() が定数であることを意味する。 これを (*) へ代入することで
が定数であることを意味する。 これを (*) へ代入することで
![]()
のように、あっという間に一般解を得る。
続いて、特異解を見ていこう。下のほうの式
![]()
を用いて求める。今使える式は、この式と元の式(*)である。 すなわち
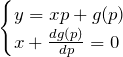
である。この2式から、![]() を消去すれば特異解が得られる。
を消去すれば特異解が得られる。
このように求めた解には定数 ![]() は含まれない。
というのも、下の式から
は含まれない。
というのも、下の式から
![]()
と、![]() を
を ![]() の関数で表すことができ、上の式へ代入することで
の関数で表すことができ、上の式へ代入することで
![]()
となる。![]() が入る余地がない。
が入る余地がない。
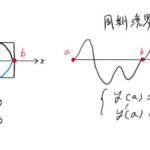
曲線群と包絡線との関係
で、結局この特異解は何だろうか。考えてみる。
*包絡線がどんなもので、求め方がわかっていると以下の説明はすんなり入ってくる。よくわからなくても、例題の解答のところで示した図をみれば、一般解と特異解の関係が綺麗になっていることはわかるだろう。
まず、式(*)を変形して
![]()
のように ![]() の3変数とみる。 これを
の3変数とみる。 これを ![]() で偏微分してみる。
で偏微分してみる。
![]()
このように ![]() を用いると
を用いると
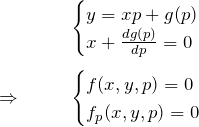
となる。この2式から ![]() を消して特異解を求めたのであった。それはつまり、
を消して特異解を求めたのであった。それはつまり、
曲線群 ![]() の包絡線を求める方法
の包絡線を求める方法
と同じである。つまり、
クレローの微分方程式の特異解は 曲線群 ![]() の包絡線で表される
の包絡線で表される
ということである。
ところで、包絡線の式 (上の2式)における ![]() は媒介変数であった。 したがって、
は媒介変数であった。 したがって、![]() の定数と見て良い。そうすると、
の定数と見て良い。そうすると、
曲線群 ![]() とは微分方程式の一般解を表している
とは微分方程式の一般解を表している
ということである。
以上のことをまとめると、 クレローの微分方程式の特異解は、一般解を曲線群とする包絡線に対応する。 この綺麗な関係についてあとの例題でも確認する(図を参照)。ここに書いてあることがわからなくても、なんとなく図が綺麗に見えると思う。
解法まとめ
クレローの微分方程式は、一般解と特異解を求める必要がある。流れは以下の通りである。
![]()
- (*)の両辺を
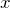 で微分する(
で微分する(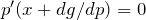 )
) -
 と (*) から一般解
と (*) から一般解 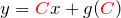
- 特異解は、以下の式から媒介変数
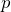 を消去することで得る
を消去することで得る
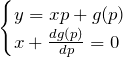
2. 例題の解答
以下の解答で ![]() は定数を表す。
は定数を表す。
例題(1)の解答
![]()
の両辺を ![]() で微分する。
で微分する。
![]()
一般解:
![]() より、一般解
より、一般解
![]()
特異解:
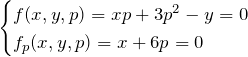
したがって
![]()
を用いて ![]() を消去すると
を消去すると
![]()
これが特異解である。
*一般解と特異解の関係が、曲線群と包絡線の関係になっていることは下の図より確認できる。
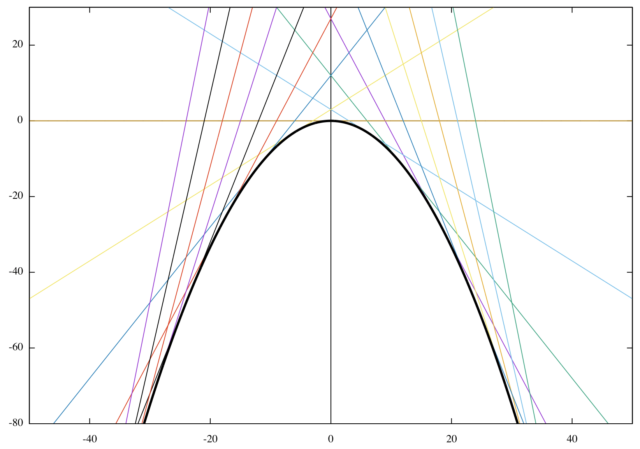
例題(2)の解答
![]()
の両辺を ![]() で微分する。
で微分する。
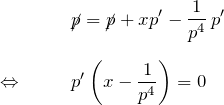
一般解:
![]() を元の微分方程式へ代入して
を元の微分方程式へ代入して
![]()
特異解:
![]()
を元の微分方程式へ代入して
![]()
これが特異解となる。
*一般解と特異解の関係が、曲線群と包絡線の関係になっていることは下の図より確認できる。
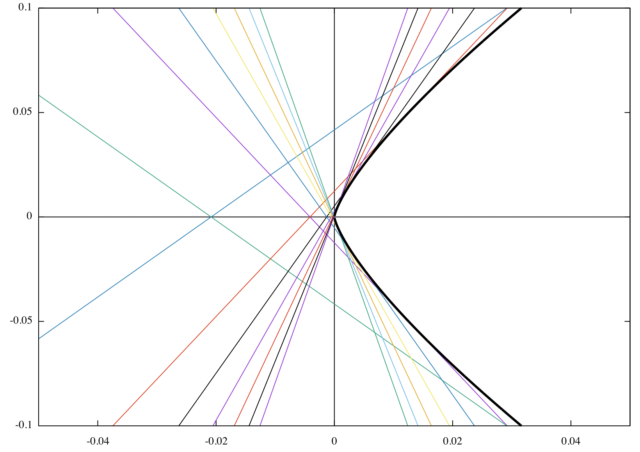
例題(3)の解答
![]()
の両辺を ![]() で微分して
で微分して
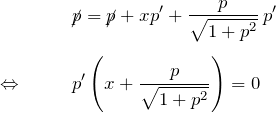
一般解:
![]() を元の微分方程式へ代入して
を元の微分方程式へ代入して
![]()
特異解: ![]() を消去する。ここでは少し工夫して消去する。
を消去する。ここでは少し工夫して消去する。
![]()
を元の微分方程式へ代入する。
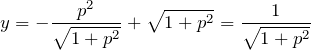
これより、![]() である。また、
である。また、
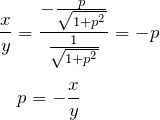
である。これを ![]() へ代入して
へ代入して
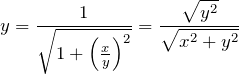
![]() より
より
![]()
を得る。したがって、![]() より
より
![]()
が特異解となる。
*一般解と特異解の関係が、曲線群と包絡線の関係になっていることは下の図より確認できる。
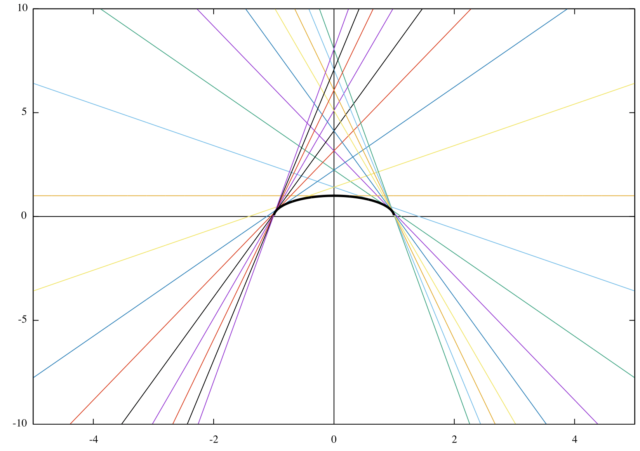
3. まとめ
とにかく、与えられた微分方程式の両辺を ![]() で微分すれば、なんとか自力で解けるかもしれない。 特異解が包絡線になっていることを知っているとクレローの微分方程式も楽しく解くことができるだろう。
で微分すれば、なんとか自力で解けるかもしれない。 特異解が包絡線になっていることを知っているとクレローの微分方程式も楽しく解くことができるだろう。