包絡線の求め方を例題を通して習得する。求め方は媒介変数を消去すればいいのだが、なぜだろうか。ここでは、包絡線について説明して、その求め方を解説していく。最後に例題の解答を行う。例題は以下の通り。
以下の曲線群の包絡線を求めよう(![]() はパラメータ)。
はパラメータ)。
![]()
目次
1. 包絡線とは何か
包絡線について簡単に説明する。
逆から考える
包絡線を求めるとは、与えられた「曲線の集まり」に接する曲線を求めることである。 逆から考えると、包絡線の各点の接線は与えられた「曲線の集まり」になる。
放物線を例にとって見てみる。放物線のある点での接線を求める問題は高校でよく習う。 下図の真ん中に、いろいろな点で接線を求めてみた場合を書いた。
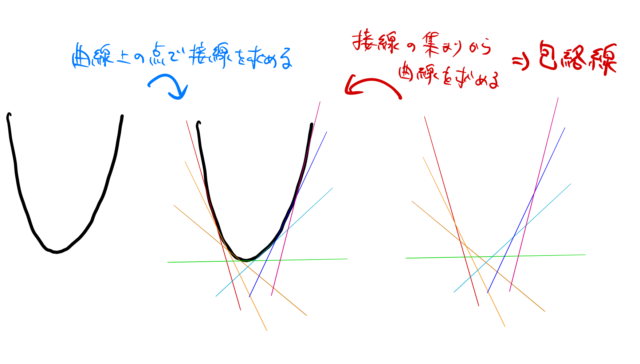
図の右のように、得られた接線の集まりから元の放物線を消し去ってみよう。 包絡線を求める問題は、 「元の放物線を取り戻す」 ことである。
いくつかの包絡線の例
実際には、与えられる曲線群は接線とは限らない。ここでは例として、楕円群や放物線群の包絡線を下に示しておこう。
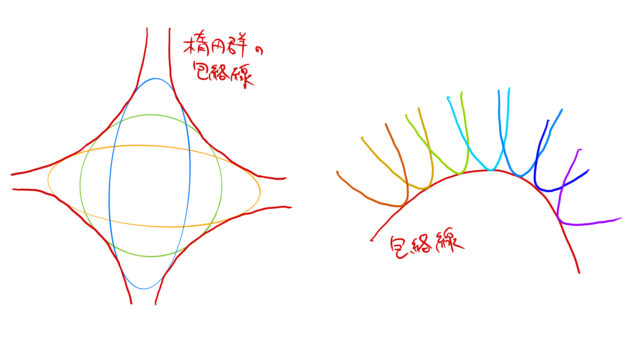
2. 包絡線の求め方
1本の接線が定まる条件と「特異点」
与えられた曲線
![]()
について、ある点で1本の接線がある条件を考える。
この式を微分すると
![]()
である。したがって、![]() のとき、
のとき、
![]()
の傾きを持った接線が存在する。また、![]() であっても、
であっても、![]() であれば、
であれば、
![]()
の接線が存在する。
したがって、1本の接線が定まらない条件は ![]() が
が
![]()
となる点である。この点を特異点と呼ぶ。 つまり、特異点では接線が存在しない。
曲線群の表し方と媒介変数(パラメータ)
例として楕円を考える。楕円
![]()
は楕円群
![]()
の中に含まれている。つまり、![]() のときの楕円である。
のときの楕円である。
上の楕円を表す曲線を
![]()
とすれば楕円群を表す式は
![]()
となる。曲線群は ![]() で表すことができ、
で表すことができ、![]() を変えることによって色々な曲線を作ることができる。
を変えることによって色々な曲線を作ることができる。
包絡線を求めるための条件を考える。まず曲線群の中から![]() に対応する2つの曲線を考える。
に対応する2つの曲線を考える。
![]()
2つの曲線の交点は
![]()
である。
この式は ![]() であるため、
であるため、
![]()
とかける。ここで、![]() とする。つまり、一方の曲線の形をもう一方の曲線に限りなく近づける。
とする。つまり、一方の曲線の形をもう一方の曲線に限りなく近づける。
![]()
この条件は考えている2曲線に関する条件である (ちょっとズレた2曲線に接する曲線を求めるイメージ)。 実際には無数にある曲線に接する曲線(包絡線)を求めたい。 したがって、曲線群に対しては
![]()
の条件を課す。
以上をまとめて
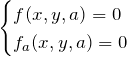
から媒介変数(パラメータ) ![]() を消去して、曲線群
を消去して、曲線群 ![]() の包絡線を得る。
の包絡線を得る。
*見ての通り2条件ある。そのイメージを書いておく。
まず ![]() を固定して、何かの曲線を考えよう。
1番目の式が「考えている
を固定して、何かの曲線を考えよう。
1番目の式が「考えている ![]() の曲線に接する(交点を持つ)」条件で、
2番目の式が、「考えている
の曲線に接する(交点を持つ)」条件で、
2番目の式が、「考えている ![]() の曲線とその隣の
の曲線とその隣の ![]() の2曲線に接する」条件である。
実際には無数に
の2曲線に接する」条件である。
実際には無数に ![]() があるため、媒介変数としての
があるため、媒介変数としての ![]() は消去される。
は消去される。
包絡線の求め方まとめ
解き方をまとめておこう。
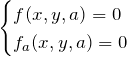
![]()
3. 例題の解答
(2)は特異点を除くことを忘れないように。
例題(1)の解答
与えられた曲線群:
![]()
これは放物線であるため特異点はない。
![]() の形(条件1):
の形(条件1):
![]()
![]() の形(条件2):
の形(条件2):
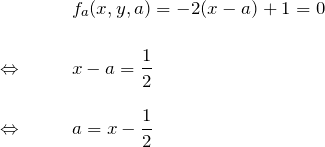
![]() を消去(条件1へ代入):
を消去(条件1へ代入):
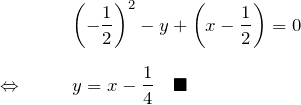
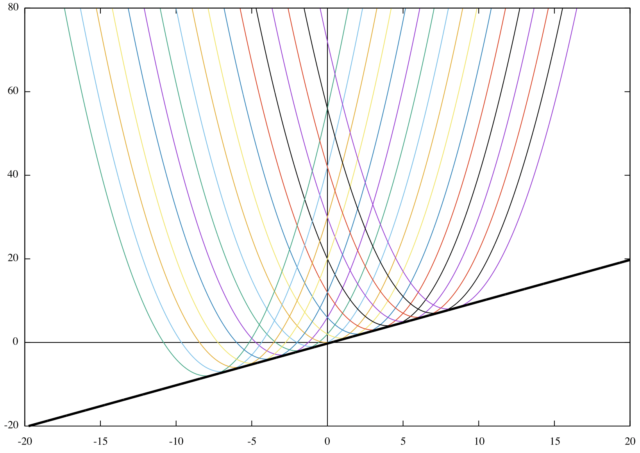
*与えられた放物線群の一部と求めた包絡線 ![]() を下図に示す。
を下図に示す。
例題(2)の解答
与えられた曲線群:
![]()
![]() の形(条件1):
の形(条件1):
![]()
![]() の形(条件2):
の形(条件2):
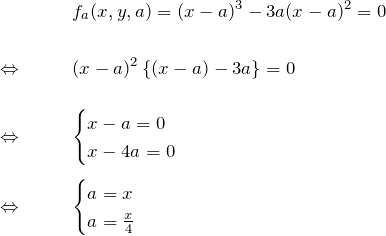
![]() を消去(条件1へ代入):
(i)
を消去(条件1へ代入):
(i) ![]() のとき、
のとき、
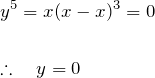
したがって、![]() となり、直線
となり、直線 ![]() を得る。
ここで、
を得る。
ここで、
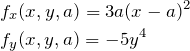
より、![]() は
は
![]()
を満たす。つまり曲線群 ![]() の特異点である。
の特異点である。
(ii) ![]() のとき、
のとき、
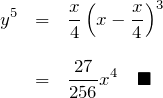
これが求める曲線群の包絡線である。
*与えられた曲線群の一部と求めた包絡線 ![]() を下図に示す。
を下図に示す。
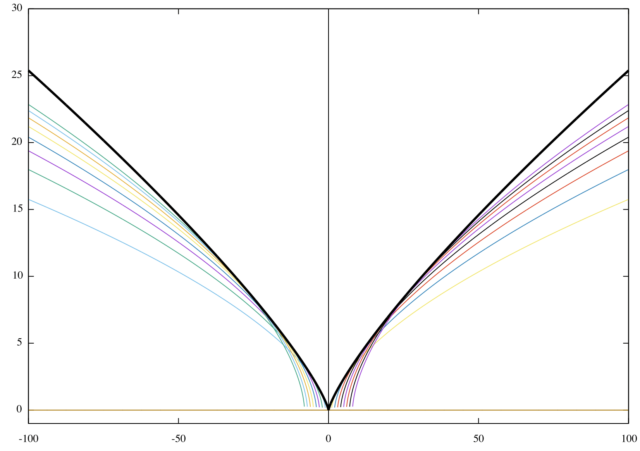
4. まとめ
包絡線の求め方は、媒介変数を消去するだけなので簡単である。 いろいろな例題を解いて、包絡線を求められるようにしておくとよい。
素晴らしい。