ラプラス変換は微分方程式を解くための道具でしかない。ここでは、面倒な積分計算は書かずにイメージだけ伝えたい。ラプラス変換の応用の要点は
- 微分方程式・積分方程式を簡単に解くために遠回りする
ということである。
解きたい方程式の形
微分方程式は物理でよく登場する。よくある運動方程式
![]()
も微分方程式である。この場合は、力 ![]() によって物体の位置
によって物体の位置 ![]() がどのように変化していくかを記述している。
がどのように変化していくかを記述している。
つまり、時間 ![]() に関する微分方程式の場合は、物理現象などがどのように変化しているかを表しているにすぎない。したがって、物理現象を表す微分方程式を解いて、物理現象を理解したいのである。
に関する微分方程式の場合は、物理現象などがどのように変化しているかを表しているにすぎない。したがって、物理現象を表す微分方程式を解いて、物理現象を理解したいのである。
ラプラス変換が便利な場面はこの微分方程式を解くときである。
遠回りのイメージ
下の図を見て欲しい。
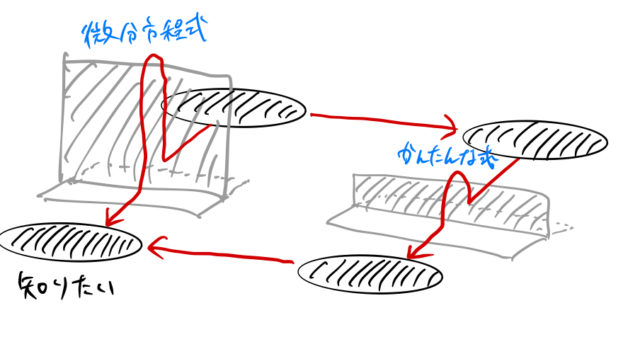
微分方程式を解くにはハードルが高すぎる。なんとかハードルが低いところを通りたい。このハードルの低い場所へ移動するために使われるのがラプラス変換やフーリエ変換である![]() 。
。
もっと具体的なイメージを描いてみる。下のようにラプラス変換によって時間 ![]() の世界から
の世界から ![]() の世界に移される。
の世界に移される。
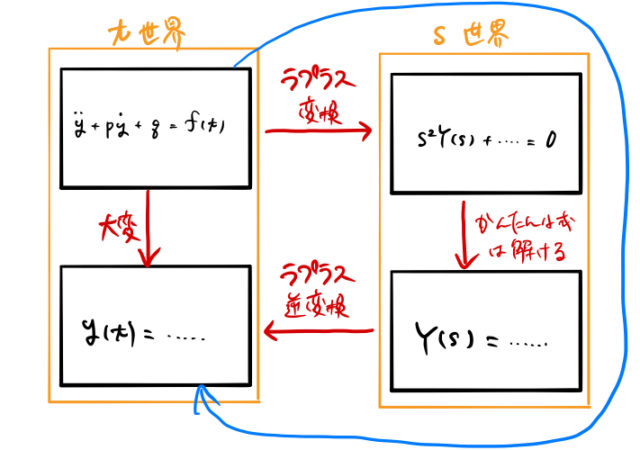
ラプラス変換による道筋
ラプラス変換を用いて微分方程式を解く場合のプロセスは下の通り。これは青色の矢印をたどればよい。
- 微分方程式をラプラス変換(
 世界へ)
世界へ)  世界の代数方程式(二次方程式など)を解く
世界の代数方程式(二次方程式など)を解く- 二次方程式の解をラプラス逆変換(
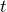 世界へ)
世界へ)
図の ![]() は求めたい
は求めたい ![]() のラプラス変換であり、
のラプラス変換であり、![]() 世界での姿である。
世界での姿である。![]() をラプラス逆変換すれば
をラプラス逆変換すれば ![]() が得られるのである。
が得られるのである。
結局ラプラス変換を用いて微分・積分方程式を解くためには、「ラプラス変換」と「ラプラス逆変換」だけ学べば良い。
なぜ簡単に解けるのか
それはラプラス変換によって、微分積分という面倒な計算が代数方程式に置き換わるからである!ここで、代数方程式の左辺の次数は、
- 一階微分方程式 → 一次方程式
- 二階微分方程式 → 二次方程式
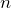 階微分方程式 →
階微分方程式 → 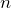 次方程式
次方程式
であることが知られている。微分方程式の右辺が0であれば、簡単に解くことができる。
しかし右辺が0でない場合は、ラプラス変換後の右辺は分数になったり、指数になったりと暴れがちである。そのような問題は逆変換のパターンを習得して、問題演習で慣れていくしかない。
最後に定義だけ書いておく
![]() 世界への移す方法、つまり、ラプラス変換の定義を書いておく。
世界への移す方法、つまり、ラプラス変換の定義を書いておく。
![]()
単に、![]() 世界に移したい関数
世界に移したい関数 ![]() に
に ![]() をかけて
をかけて ![]() で積分する、だけである。ピエール=シモン・ラプラスがこういう風にすれば、うまく微分方程式がとけるぞ、ということで定義した式に過ぎない。
で積分する、だけである。ピエール=シモン・ラプラスがこういう風にすれば、うまく微分方程式がとけるぞ、ということで定義した式に過ぎない。
悩むより「こういう変換をすればうまくいったんだ」くらいの心持ちで勉強するのがラプラス変換である。ド応用数学である。
![]() :フーリエ変換は
:フーリエ変換は ![]() の変換で時間空間と周波数空間を行き来する。したがって物理的意味がはっきりしている。しかし、ラプラス変換の場合はあまり物理的意味が感じられない。やはり、微分方程式を解くための道具という印象である。
の変換で時間空間と周波数空間を行き来する。したがって物理的意味がはっきりしている。しかし、ラプラス変換の場合はあまり物理的意味が感じられない。やはり、微分方程式を解くための道具という印象である。