以下のディリクレ積分と呼ばれる実積分を複素関数を用いた複素積分で解く。
ディリクレ(Dirichlet)積分
![]()
1. 複素積分の積分経路
誰か偉い人が考えた積分経路によって解く。
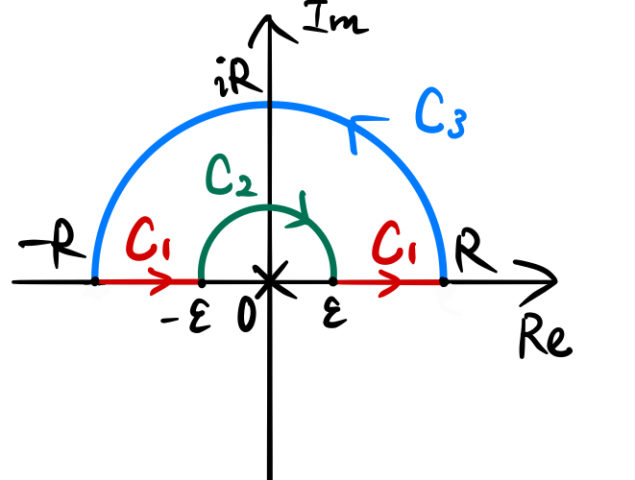
最終的には以下のようになる。
 :
: で求める実積分に対応
で求める実積分に対応 :
: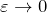 で
で 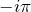 に収束
に収束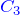 :
: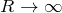 で
で 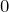 に収束
に収束
2. 解答
![]() は
は ![]() より、
より、
![]()
と変形できる。ここで、![]() と置く。上に与えた積分経路で複素積分すると、
と置く。上に与えた積分経路で複素積分すると、
![]()
ここで、左辺の周回積分 ![]() について考える。この積分は、
について考える。この積分は、![]() の積分経路内に特異点がない(領域内で正則である)ために積分値は 0 になる【コーシー(Cauthy)の積分定理】。
の積分経路内に特異点がない(領域内で正則である)ために積分値は 0 になる【コーシー(Cauthy)の積分定理】。
C1上の複素積分
![]() は実軸上であるため、
は実軸上であるため、![]() になる。
になる。
また、![]() は2つの部分に分かれている。つまり、積分は
は2つの部分に分かれている。つまり、積分は ![]() と
と ![]() の積分に分けることができる。
の積分に分けることができる。
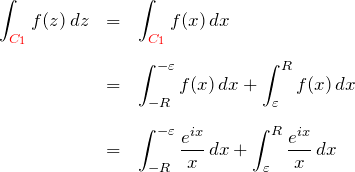
ここで第1項について、![]() と置くと、
と置くと、
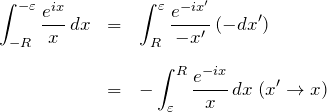
最後の行で、積分変数 ![]() を置き換えと積分経路の入れ替えをおこなった。これより、
を置き換えと積分経路の入れ替えをおこなった。これより、
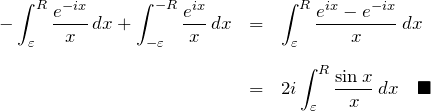
この積分は、![]() で求める実積分(Dirichlet積分)に一致する。
で求める実積分(Dirichlet積分)に一致する。
C2上の複素積分
![]() について、
について、![]() まわりで
まわりで ![]() をテイラー展開して、
をテイラー展開して、![]() で割る。
で割る。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{e^{iz}}{z}&=&\frac{1}{z} \left[1+(iz)+\frac{1}{2!}(iz)^2+\frac{1}{3!}(iz)^3+\cdots\right]\\\\ &=& \frac{1}{z}+i\left[1+\frac{1}{2!}(iz)+\frac{1}{3!}(iz)^2+\cdots\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f35e181d50179c08a8c2e6f49b94cdcf_l3.png)
よって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{\textcolor{green}{C_2}} f(z)\,dz&=& \int_{\textcolor{green}{C_2}}\frac{dz}{z} \,dz\\\\&+& i\int_{\textcolor{green}{C_2}}\left[1+\frac{1}{2!}(iz)+\frac{1}{3!}(iz)^2+\cdots\right]\,dz\\\\ \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2d8f32ca80febb224fd7de4118bb2eed_l3.png)
以下では ![]() とおいて積分を計算する。ただし、最後に
とおいて積分を計算する。ただし、最後に ![]() とする。
とする。
第一項:
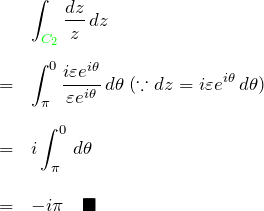
第二項:
![]()
の ![]() の収束性を調べる。計算のポイントは以下の通り。
の収束性を調べる。計算のポイントは以下の通り。
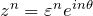
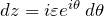
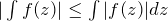
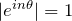 :単位円を表すため絶対値は
:単位円を表すため絶対値は 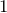
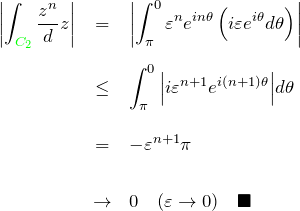
まとめると、![]() で
で
![]()
C3上の複素積分
![]() での積分の絶対値が収束するか調べる。
での積分の絶対値が収束するか調べる。
![]()
を用いて、
複素積分の結果をまとめる
![]() として、
として、
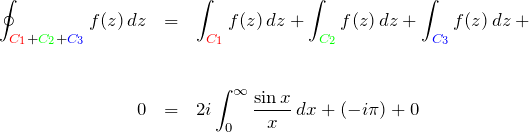
したがって、
ディリクレ(Dirichlet)積分
![]()
を得る。![]()
3. まとめ
留数定理を使わないタイプの複素積分の応用であった。積分経路が複雑であることと収束を調べることがポイントだろう。
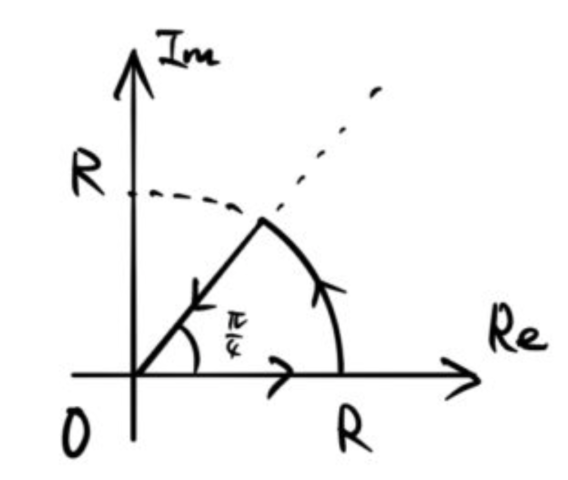
C3の■の下から2行目、θのところはπの誤植です。