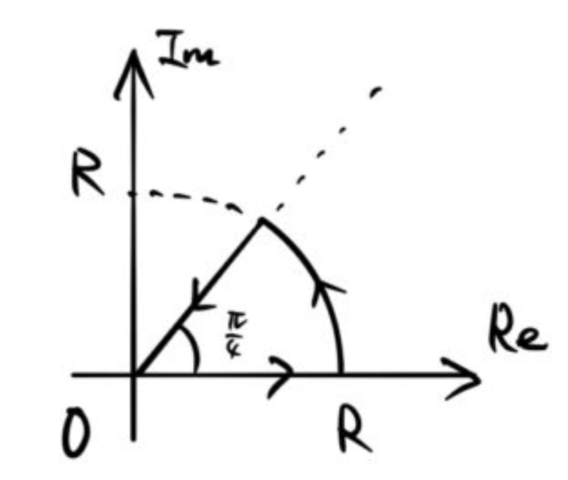
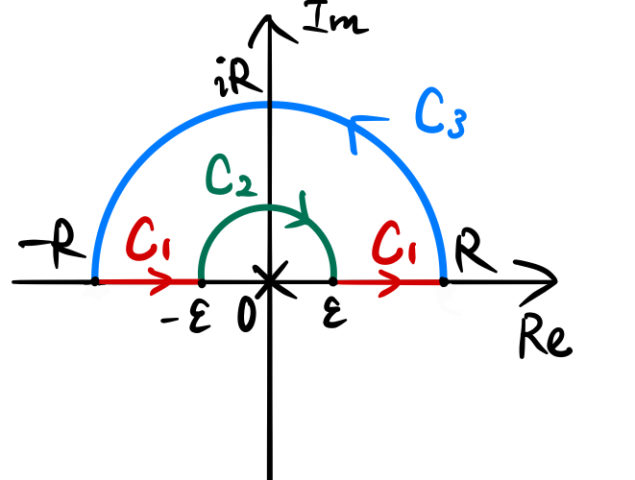
複素積分の応用問題を解く。 ここで学ぶことは、
- 留数定理の応用
- 実積分を複素積分で解く
である。
有名な問題としてを積分しよう。
例題
(1) 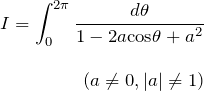
1. 複素積分に変換して解く
積分区間は ![]()
とおく。このとき、
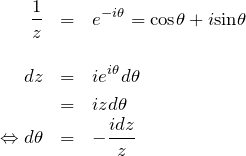
である。![]() を
を ![]() で表すと、
で表すと、
(2) ![]()
cosやsinの実積分から複素積分へ
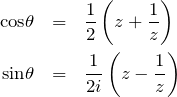
複素積分の変換により求めたい積分は、
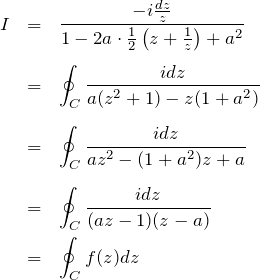
2. 極を求めて留数定理を用いる
分母がゼロになる特異点である極は2つある。それぞれ1位の極で、
(3) ![]()
複素関数 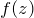 の1位の極
の1位の極 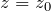 の留数
の留数
![]()
(i) ![]() の留数:
の留数:
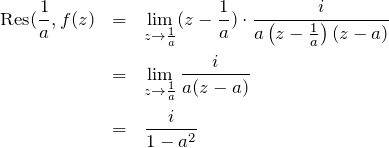
(ii) ![]() の留数:
の留数:
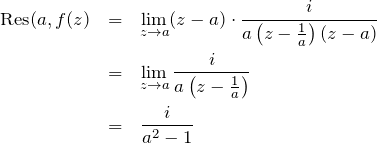
留数がわかったので、留数定理により求めたい積分 ![]() を計算する。ただし、留数定理の適用は、極が積分領域
を計算する。ただし、留数定理の適用は、極が積分領域 ![]() (複素平面上の単位円)の内側にある極についてのみ
(複素平面上の単位円)の内側にある極についてのみ ![]() として使えるのであった。(「コーシーの積分公式」を思い出してもらえればわかる。)
として使えるのであった。(「コーシーの積分公式」を思い出してもらえればわかる。)
(I) ![]() のとき:
のとき:
このとき、![]() であり、
であり、 ![]() の外にある。したがって、
の外にある。したがって、![]() の極についてのみ、留数定理を用いる。
の極についてのみ、留数定理を用いる。
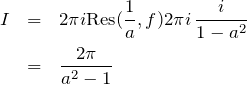
(II) ![]() のとき:
のとき:
このとき、![]() であり、
であり、![]() の外にある。したがって、
の外にある。したがって、![]() の極についてのみ、留数定理を用いる。
の極についてのみ、留数定理を用いる。
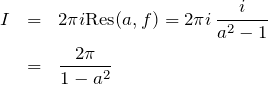
である。まとめて書くと、
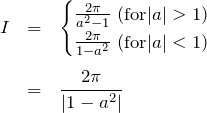
3. まとめ
一般に、![]() の実積分を複素積分に変換するとうまく解けることがある。複素積分を計算する上で、留数定理が強力な武器になることも確認できたであろう。
の実積分を複素積分に変換するとうまく解けることがある。複素積分を計算する上で、留数定理が強力な武器になることも確認できたであろう。