ここでは、全微分の形がどうか調べる方法を学ぶ。 応用として、完全微分型の微分方程式を解く上で非常に重要である。
ある関数が全微分になっているか調べるためには、以下の条件を用いると良い。
ポイント
が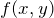 の全微分
の全微分 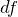 であるための必要十分条件は
であるための必要十分条件は
が成立することである。
ある関数
![]()
が
![]()
が成立することである。
1. 全微分の定義
2変数関数の場合の全微分の形をまとめておく。 ![]() の全微分は以下のように
の全微分は以下のように ![]() の偏微分によって表される。
の偏微分によって表される。
ポイント
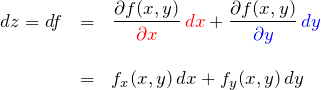
これは基本なのでおさえておく。
2. 証明
必要条件、十分条件についてそれぞれ証明していく。
必要条件
![]() が
が ![]() の全微分 (
の全微分 (![]() ) のとき、
) のとき、
![]()
となることを示す。
【証明】
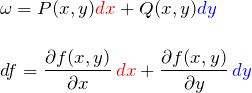
について、![]() が独立であるため
が独立であるため ![]() のとき
のとき
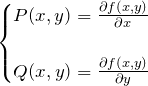
上を ![]() で偏微分、下を
で偏微分、下を ![]() で偏微分して
で偏微分して
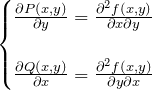
となる。
したがって、
![]()
となる。
十分条件
![]()
のとき ![]() は
は ![]() の全微分(
の全微分(![]() )になることを示す。 何の関数になっているかに注意して証明していく(
)になることを示す。 何の関数になっているかに注意して証明していく(![]() など)。
など)。
【証明】
![]()
が成立する。
このとき、
![]()
とおく。![]() で偏微分して
で偏微分して
![]()
を得る。
これをさらに、![]() で偏微分して
で偏微分して
![]()
となる。
![]() でまとめる。
でまとめる。
![]()
![]() で偏微分して0になるため、カッコの中は
で偏微分して0になるため、カッコの中は ![]() を含まない
を含まない ![]() のみの関数である。よって
のみの関数である。よって
![]()
とおく。
ここで
![]()
とおく。
このとき
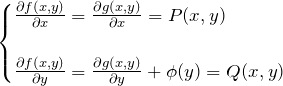
となる。したがって、
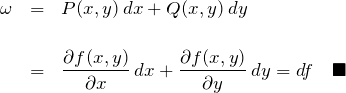
となる。
3. まとめ
完全微分型の微分方程式を学ぶときに、ここの内容を思い出してあげて。