1. 解答
入試問題は各自で入手すること。答えのみ(証明は略)。
【問題1】4項間漸化式・固有値方程式
3次の正方行列の中に0が複数ある場合、行列式を求めるときはサラスの法則を使う。あるいは余因子展開を行う。
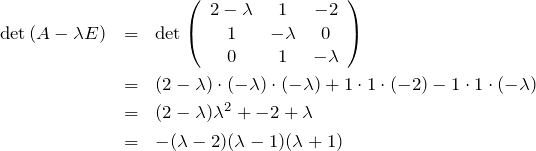
det![]() として、固有値
として、固有値![]() を得る。固有値が間違っていないかの検算は下の関係を使うと良い。確かに
を得る。固有値が間違っていないかの検算は下の関係を使うと良い。確かに ![]() となっている。
となっている。
![]() 次の正方行列Aとその
次の正方行列Aとその![]() 個の固有値に対して、
個の固有値に対して、
(i) ![]() のとき
のとき
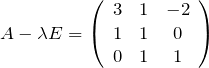
固有ベクトルを探す。つまり、
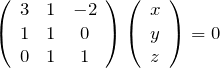
を満たす
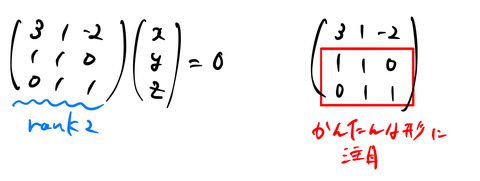
rank2であるので、たとえば1行目は(2行目)![]() 3-(3行目)
3-(3行目)![]() 2で作られる。だから、赤色の部分の連立方程式を解けば良い。未知数3(
2で作られる。だから、赤色の部分の連立方程式を解けば良い。未知数3(![]() )に対して、行列のrankは2なので、解の自由度は1である。念の為、連立方程式を書いておく。
)に対して、行列のrankは2なので、解の自由度は1である。念の為、連立方程式を書いておく。
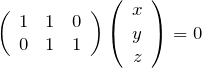
この解の1つを見つければよい。つまり、後のために簡単な解
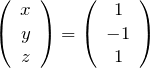
固有ベクトルの向きは(1,-1,1)方向である。解の自由度1であるのでベクトルの大きさ![]() は任意である。問題に指定がなければ、
は任意である。問題に指定がなければ、![]() の任意性があるので計算が簡単になる固有ベクトルを選べる。規格化された固有ベクトルを求める場合は
の任意性があるので計算が簡単になる固有ベクトルを選べる。規格化された固有ベクトルを求める場合は![]() とする。
とする。
(ii) ![]() のとき
のとき
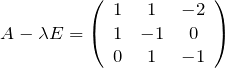
固有ベクトルを探す。2行目、3行目の簡単な形に着目すると解の1つは容易に、(1,1,1)とわかる。それを規格化して、![]() に対する固有ベクトルは、
に対する固有ベクトルは、
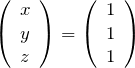
となる。
(iii) ![]() のとき
のとき
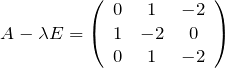
固有ベクトルを探す。2行目、3行目(or 1行目)の簡単な形に着目すると解の1つは容易に、(4,2,1)とわかる。それを規格化して、![]() に対する固有ベクトルは、
に対する固有ベクトルは、
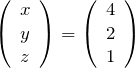
となる。
行列Aの対角化
上で得られた3つの固有ベクトルを並べて、
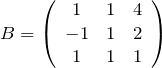
を作る。![]() の逆行列
の逆行列 ![]() は基本行列変形
は基本行列変形 ![]() (掃き出し法)により求める。最終結果は、
(掃き出し法)により求める。最終結果は、
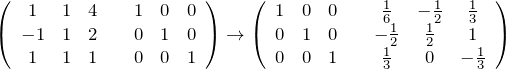
なので、
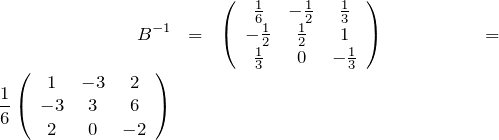
である。(![]() のチェックを忘れずに。)Bを用いて、
のチェックを忘れずに。)Bを用いて、![]() の対角化は
の対角化は
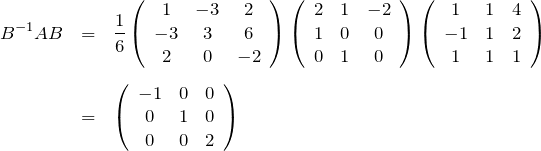
のようになる。
固有値![]() の順番に固有ベクトルを並べて行列
の順番に固有ベクトルを並べて行列![]() を作ったので、
を作ったので、![]() の対角化により対角要素は固有値
の対角化により対角要素は固有値![]() の順番に並ぶ。
の順番に並ぶ。
4項間漸化式を行列で表す。
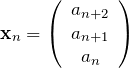
と置くと、行列![]() を用いて与えられた漸化式は、
を用いて与えられた漸化式は、
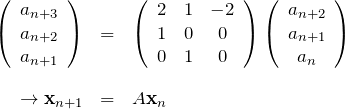
となる。左から ![]() をかけて、
をかけて、
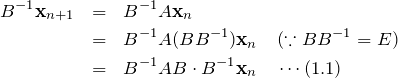
となる。ここで、
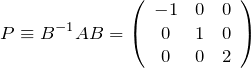
である。行列 ![]() は対角行列であるので、
は対角行列であるので、
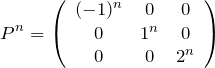
である。式(1.1)より、
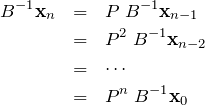
となる。左辺の ![]() を消すために、左から
を消すために、左から![]() をかけて、
をかけて、
![]()
を得る。![]() を計算する。
を計算する。
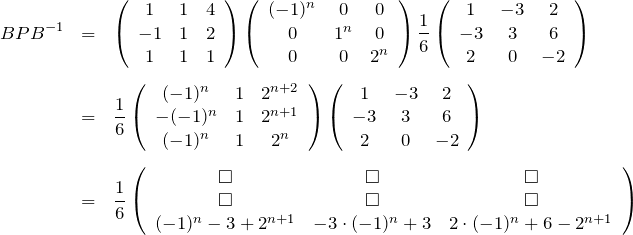
使うのは3行目だけなので、その成分を示した。式(1.3)より、
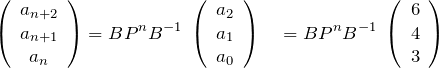
となる。よって求める一般項 ![]() (
(![]() は0以上の整数)は、
は0以上の整数)は、
![Rendered by QuickLaTeX.com \begin{eqnarray*} a_n &=&\frac{1}{6}\left[(-1)^n-3+2^{n+1} \right]\cdot 6\\ &+&\frac{1}{6}\left[-3\cdot (-1)^n+3 \right]\cdot 4\\ &+&\frac{1}{6}\left[2\cdot (-1)^n + 3 \cdot 2^{n+1}\right]\cdot 3 \\ \\ &=&\frac{1}{6}\left[12+3\cdot 2^{n+1} \right] \\ \\ \therefore \quad a_n &=&2+2^n\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-87019e54b4a43cb1b15d36b99c8aa7a9_l3.png)
確かに、![]() 、
、![]() 、
、![]() となる。
となる。
補足:行列を利用しない方法:題意に沿わないが一般項は容易に求められる。
![]()
について![]() と置いて、
と置いて、
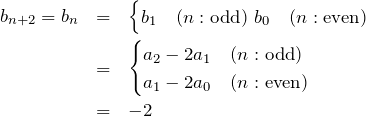
となる。よって、
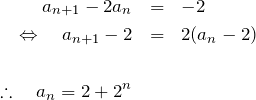
のように一般項が求められる。この問題ような特殊な4項間漸化式については、うまく変形できれば容易に一般解が求められる。
【問題2】回転体の体積・表面積
(1) まず変数分離型の微分方程式を解く。![]() を定数として、
を定数として、
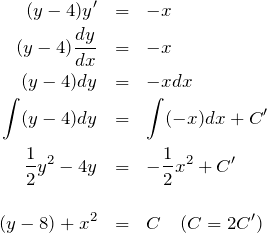
![]() を代入すると、
を代入すると、![]() が求まる。
が求まる。
![]() のとき、
のとき、![]()
求める円の方程式は、
![]()
であり、中心 (0,4)で半径2の円である(図は略)。
(2) 与えられた式に![]() を代入する。
を代入する。
![]() での微分係数を、
での微分係数を、![]() と書く。
と書く。
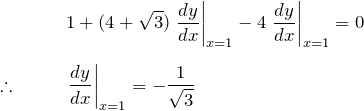
したがって、与えられた点の接線の方程式は、
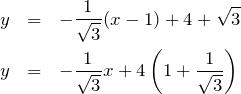
である。
(3) (4) トーラスの体積・表面積の計算はパップス=ギュルダンの定理を使うと求められる。
【問題3】フーリエ変換・δ関数
(1) ![]() をフーリエ変換する。
をフーリエ変換する。
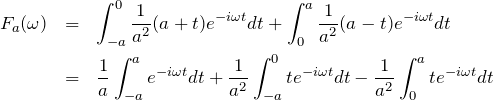
第一項:
![Rendered by QuickLaTeX.com \begin{eqnarray*}\frac{1}{a}\int_{-a}^{a} e^{-i\omega t}dt&=&\left[ \frac{1}{-i\omega} e^{-i\omega t} \right]_{-a}^{a}\\&=& \frac{1}{a}\frac{i}{\omega}\left( e^{-i\omega a}-e^{i\omega a}\right)\\&=& \frac{2}{\omega a}{\rm sin}\left( \omega a \right)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-04c270dea0d8b2f35b2cc701dccd1ccb_l3.png)
第二項:
![Rendered by QuickLaTeX.com \begin{eqnarray*}&&\frac{1}{a^2}\int_{-a}^{0} t e^{-i\omega t}dt - \frac{1}{a^2}\int_{0}^{a} t e^{-i\omega t}dt \\&=&\frac{1}{a^2}\int_{a}^{0} (-t') e^{i\omega t'}(-dt') -\frac{1}{a^2}\int_{0}^{a} t e^{-i\omega t}dt \quad (\because t=-t') \\ &=&-\frac{1}{a^2}\int_{0}^{a} t' e^{i\omega t'}dt' -\frac{1}{a^2} \int_{0}^{a} t e^{-i\omega t}dt \\ &=&-\frac{1}{a^2}\int_{0}^{a} t\left(e^{i\omega t} + e^{-i\omega t} \right) dt\\ &=& -\frac{2}{a^2}\int_{0}^{a} t{\rm cos}(\omega t)dt \\ &=&-\frac{2}{a^2} \left[ \frac{t}{\omega} {\rm sin}(\omega t) + \frac{1}{\omega} {\rm cos}(\omega t)\right]_0^{a} \\&=&-\frac{2}{\omega a}{\rm sin}(\omega a) - \frac{2}{\omega a^2}{\rm cos}(\omega a) + \frac{2}{\omega a^2}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-db1bf88d3d1db20b5ed6e65d8b4ca76f_l3.png)
以上より、
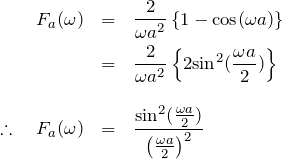
この関数は、回折で現れる1次元のラウエ関数と同じ形をしている。
(2) ![]() の極限を取る
の極限を取る![]() のとき、
のとき、
![]()
![]() のとき、
のとき、![]() の定義より、
の定義より、
![]()
よって、
![]()
である。また、![]() 軸と
軸と![]() で囲まれる三角形の面積は、
で囲まれる三角形の面積は、
![]()
であるので、
![]()
(3) 複素フーリエ係数を求める。
![]() の区間をフーリエ変換すれば良い。
の区間をフーリエ変換すれば良い。
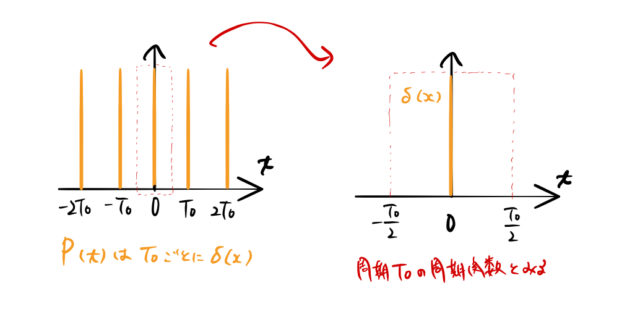
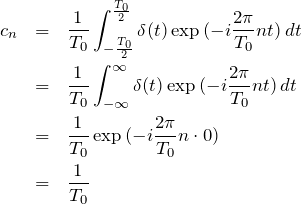
から、
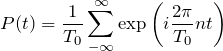
となる。
(4) ![]() の両辺をフーリエ変換する。
の両辺をフーリエ変換する。
![Rendered by QuickLaTeX.com \begin{eqnarray*}H_s(\omega)&=&\int_{-\infty}^{\infty} T_0 h(t) P(t) \exp{(-i\omega t)}\,dt\\&=&T_0 \int_{-\infty}^{\infty} h(t) \left[ \frac{1}{T_0} \sum_{n=-\infty}^{\infty}\exp{\left( i\frac{2\pi}{T_0} nt \right)}\right] \exp{(-i\omega t)} \,dt\\&=&\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty} h(t)\exp{\left( i\frac{2\pi}{T_0} nt \right)}\exp{(-i\omega t)}\,dt \\&=&\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty} h(t)\exp{\left( -i\left(\omega-\frac{2\pi}{T_0} n\right)t \right)} \,dt\\&=&\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty} h(t)\exp{\left( -i\omega_n t \right)} \,dt \quad \left(\omega_n=\omega-\frac{2\pi}{T_0} n\right)\\&=&\sum_{n=-\infty}^{\infty}H(\omega_n)\\&=&\sum_{n=-\infty}^{\infty}H\left(\omega-\frac{2\pi}{T_0} n\right)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1616b7f83f0a5e9c2ae1d113660cc8e8_l3.png)
証明おわり ![]()
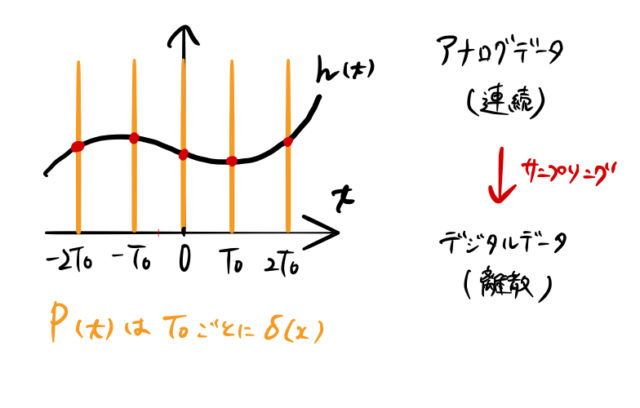
おまけ:上のようなサンプリングは、アナログデータ ![]() の値を
の値を ![]() ごとに取り出すことに対応する。つまり、フーリエ変換によってデジタルデータに変換される。情報としてデジタルデータを受け取った側は、逆フーリエ変換すれば(ほとんど)元のデータを復元することができる。
ごとに取り出すことに対応する。つまり、フーリエ変換によってデジタルデータに変換される。情報としてデジタルデータを受け取った側は、逆フーリエ変換すれば(ほとんど)元のデータを復元することができる。
【問題4】複素平面・複素積分
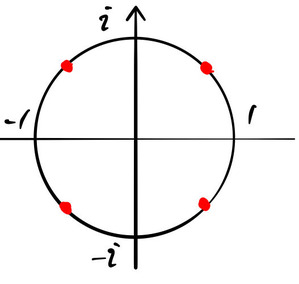
(1) 絵を描いて調べる。
図より ![]() の解は以下の通り4個ある。
の解は以下の通り4個ある。
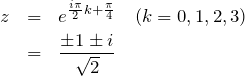
複合は任意である。
丁寧に解くなら、![]() を極形式にして解く。
を極形式にして解く。
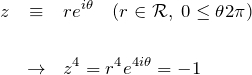
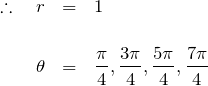
複素平面における ![]() を含む方程式は絵を描くとわかりやすい。
を含む方程式は絵を描くとわかりやすい。
(2) ![]() に置き換えて複素積分を利用する。
に置き換えて複素積分を利用する。
被積分関数は偶関数であるから積分区間を ![]() とした積分を計算する。
とした積分を計算する。
![]()
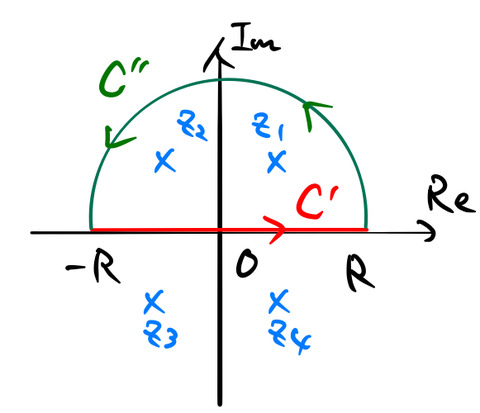
複素積分へと拡張する。積分区間は図の通り。![]() は(1)で求めた解である。
は(1)で求めた解である。
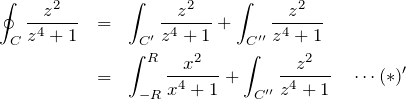
第一項の複素積分は実軸の上に経路をもつので、実積分として扱える。この項は ![]() の極限で式 (*) に一致する。左辺は留数定理より容易に計算できる。まず、複素関数
の極限で式 (*) に一致する。左辺は留数定理より容易に計算できる。まず、複素関数
![]()
は領域 ![]() 内に特異点
内に特異点 ![]() と
と ![]() をもつ。また、(1)で求めた解より、
をもつ。また、(1)で求めた解より、![]() は
は ![]() を因数にもつ。つまり、
を因数にもつ。つまり、
![]()
![]()
とする。
留数定理の計算がしやすい形に ![]() を変形する。
を変形する。
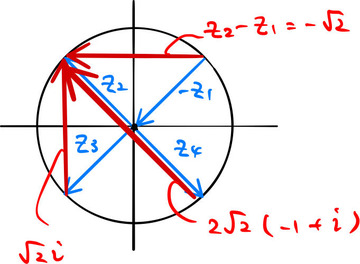
![]() に対応する留数:
に対応する留数:
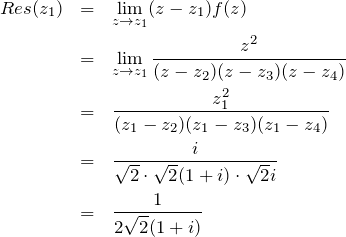
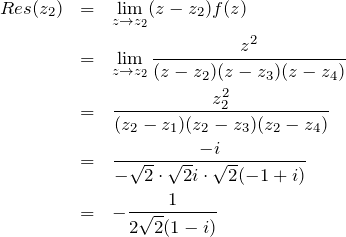
ちなみに分母の項はそれぞれ、図のようなベクトルに対応する。(![]() のときも同様)。
のときも同様)。
したがって、留数定理より、
![Rendered by QuickLaTeX.com \begin{eqnarray*}\oint_C \frac{z^2}{z^4+1} &=&2\pi i \left[Res(z_1)+Res(z_2)\right]\\&=&2\pi i \frac{1}{2\sqrt{2}} \cdot \left( \frac{1}{1+i}-\frac{1}{1-i}\right)\\&=&\frac{\sqrt{2}}{2}\pi\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-134a8cc28af1a837d754e04d8045f7f0_l3.png)
式![]() の右辺の第2項を計算する。この積分は
の右辺の第2項を計算する。この積分は ![]() の極限において0になる。なぜなら、十分大きい
の極限において0になる。なぜなら、十分大きい ![]() に対して、
に対して、![]() であるから。よって、
であるから。よって、
![]()
したがって、式![]() において
において![]() の極限をとると
の極限をとると
![]()
なので、
![]()
である。
(3) [準備中]
2. 総評
すごい計算量!