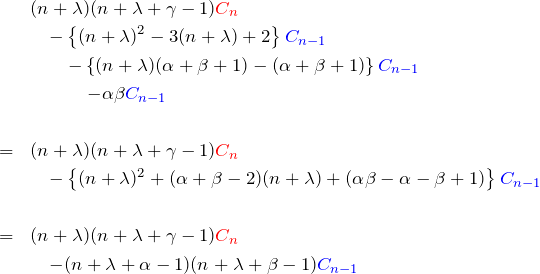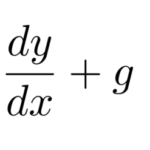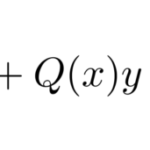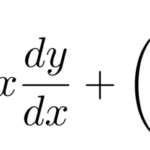一般解が以下の超幾何関数 ![]()
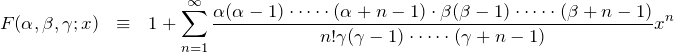
で表すことができる超幾何微分方程式(ガウスの微分方程式)
![]()
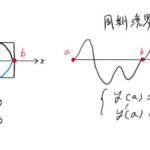
がある。この微分方程式は ![]() をもつため、「【微分方程式】確定特異点と級数の置き方/計算のコツ」が使える。この方法に従えば、超幾何関数を使う以外は普通の確定特異点をもつ微分方程式なので解くことができる。
をもつため、「【微分方程式】確定特異点と級数の置き方/計算のコツ」が使える。この方法に従えば、超幾何関数を使う以外は普通の確定特異点をもつ微分方程式なので解くことができる。
以下よりこの微分方程式を解いて、一般解を導いていこう。
1. 超幾何微分方程式を解く
- 確定特異点の説明
- 確定特異点を含む微分方程式の解法
- 級数解による解法の計算のコツ
を学んでいることが望ましい。「【微分方程式】確定特異点と級数の置き方/計算のコツ」に書いたので参考にされたい。
λを求める
![]()
は ![]() を確定特異点にもつ。したがって、級数
を確定特異点にもつ。したがって、級数
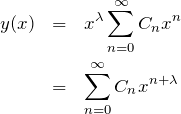
と置く。
微分:
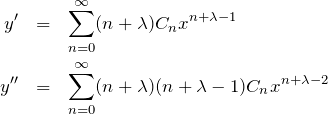
これらを微分方程式(1)に代入する。1項ずつ計算していく。
第1項:
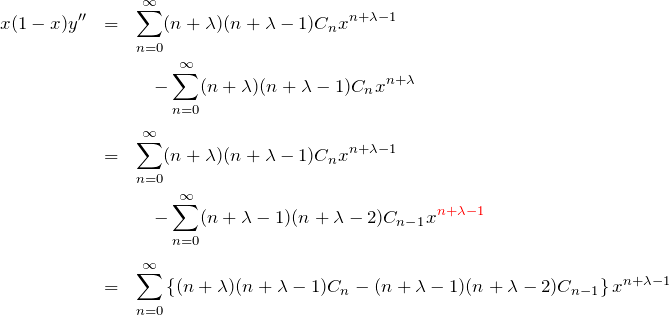
第2項:
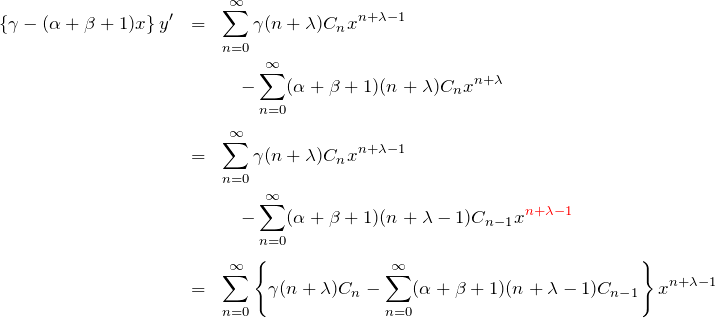
第3項:
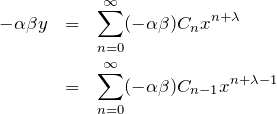
これらを元の微分方程式(1)へ代入して整理すると、![]() の係数は
の係数は
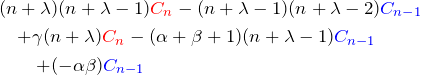
これを簡単にしたもの
を0と置いて以下を得る。
![]()
![]() と置いて(2)より、
と置いて(2)より、![]() を決める以下の決定方程式を得る。
を決める以下の決定方程式を得る。
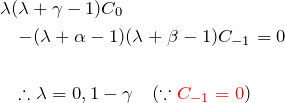
それぞれのλについての特殊解
(i) ![]() のとき:
のとき:
(2)より
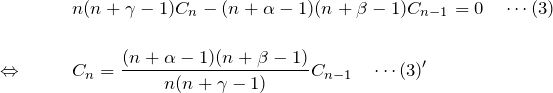
(3)’を繰り返し用いて
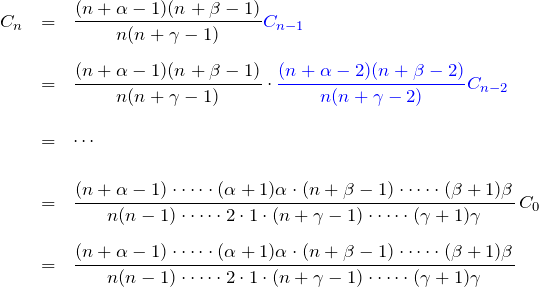
最後の行で ![]() とした
とした ![]() 。
。
したがって、![]() のときの級数解(特殊解
のときの級数解(特殊解![]() )は
)は
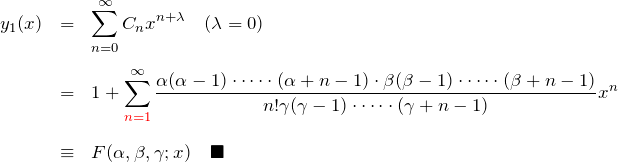
最後の行で超幾何級数 ![]() を定義した。
を定義した。
(ii) ![]() のとき:
のとき:
(2)より
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&n(n+1-\gamma)C_n -(n+\alpha-\gamma)(n+\beta-\gamma)C_{n-1}=0\\\\ \Leftrightarrow \quad&&n\bigl[n+\textcolor{magenta}{(2-\gamma)}-1\bigr]-\bigl[ n+\textcolor{red}{(\alpha-\gamma+1)}-1 \big] \bigl[ n+\textcolor{blue}{(\beta-\gamma+1)} -1\big]=0\\\\ \Leftrightarrow \quad&& n(n+\textcolor{magenta}{\gamma'}-1)-(n+\textcolor{red}{\alpha'}-1)(n+\textcolor{blue}{\beta'}-1)=0\quad\cdots(4) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-463892006441d356d311d41210cca30f_l3.png)
ここで、
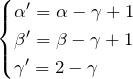
と置いた。
最後の(4)式は、(3)の形と同じ形をしている。 したがって、(i)のときの係数を ![]() とし、(ii)のときの係数を
とし、(ii)のときの係数を![]() とすると、
とすると、
![]()
となる。つまり、![]() により(i)の結果がそのまま使える。
により(i)の結果がそのまま使える。
以上より ![]() に対して、級数解(特殊解
に対して、級数解(特殊解 ![]() )は
)は
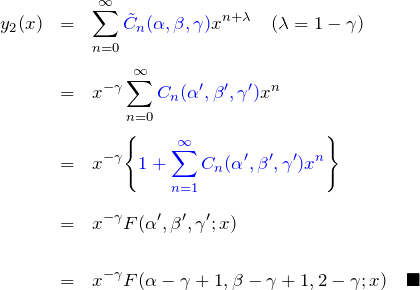
超幾何微分方程式の 一般解
したがって、一般解は ![]() (2つの特殊解)の線型結合で、
(2つの特殊解)の線型結合で、
![]()
ただし、
![]()
である(![]() は定数)。
は定数)。
*途中の「特殊解」の意味
式(3)や(4)の漸化式において、![]() とした。これは一般解のうちの
とした。これは一般解のうちの ![]() あるいは
あるいは ![]() の場合に対応する。
の場合に対応する。 ![]() を定数のまま解くこともできる。例えば、(i)
を定数のまま解くこともできる。例えば、(i) ![]() で得られた級数解を考えてみる。このとき、
で得られた級数解を考えてみる。このとき、![]() のまま用いた場合に、
のまま用いた場合に、 ![]() の代わりに得られる級数解は
の代わりに得られる級数解は
![]()
となる。つまり、![]() を定数としても得られるものは
を定数としても得られるものは ![]() の特殊解
の特殊解 ![]() の定数倍である。
の定数倍である。![]() の場合も同様に
の場合も同様に ![]() を用いれば、得られる級数解は 特殊解
を用いれば、得られる級数解は 特殊解 ![]() の定数倍となる。結局のところ
の定数倍となる。結局のところ ![]() としておいて、最後に
としておいて、最後に ![]() で定数倍したものと一致するのである。
で定数倍したものと一致するのである。
ざっくり言えば、一般解の定数を変えていろいろな解を作っていくと、特殊解 ![]() と同じものが見つかるという仕組みである。
と同じものが見つかるという仕組みである。
2. まとめ
超幾何微分方程式(ガウスの微分方程式)
![]()
の一般解は超幾何関数 ![]() を用いて
を用いて
![]()
となる。
超幾何関数の暗記は正気かな、何かのの動機があっても長期化しそう。あと、この微分方程式に関して例題を活用する人も少なそうなので、例題はつけていない。