ラゲール(Laguerre)陪多項式 ![]() について、いくつかの性質を証明付きでまとめた。ラゲール多項式
について、いくつかの性質を証明付きでまとめた。ラゲール多項式 ![]() との関係は
との関係は
![]()
である。
目次
ラゲール陪多項式の諸性質
おもに、ラゲール陪多項式 ![]() について学ぶ。
について学ぶ。
![]() の肩に
の肩に ![]() があるものが陪多項式で、
があるものが陪多項式で、![]() のものをラゲール多項式
のものをラゲール多項式 ![]() という。
という。
![]() の有無は、微分方程式の中に
の有無は、微分方程式の中に ![]() が入っているかどうかでわかる。
が入っているかどうかでわかる。
以下では、微分方程式とラゲール陪多項式について簡単にまとめた。
ラゲールの微分方程式
ラゲール陪多項式 ![]() は次の微分方程式を満たす解の1つである。
は次の微分方程式を満たす解の1つである。
![]()
ここで、![]() は整数である。微分方程式に
は整数である。微分方程式に ![]() が含まれるため、陪多項式は
が含まれるため、陪多項式は ![]() の添え字をもつ。 この式はラゲール多項式
の添え字をもつ。 この式はラゲール多項式 ![]() が満たす微分方程式
が満たす微分方程式
![]()
の両辺を ![]() で
で ![]() 回微分して、
回微分して、
![]()
を作り、
![]()
とすることで得られる。式変形の途中、![]() 回微分を実行するときにライプニッツの定理(「二項定理の微分版」のようなもの)
回微分を実行するときにライプニッツの定理(「二項定理の微分版」のようなもの)
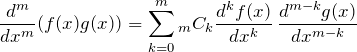
を用いた。
ラゲール陪多項式
ラゲール陪多項式 ![]() はラゲールの微分方程式を満たすである。
はラゲールの微分方程式を満たすである。
![]()
多項式の次数
ラゲール多項式 ![]() は
は
![]()
の関係があり、最高次の項は ![]() で
で ![]() は
は ![]() 次の多項式である。
陪多項式
次の多項式である。
陪多項式 ![]() は
は ![]() の
の ![]() 階微分であるので
階微分であるので ![]() 次の多項式である(
次の多項式である(![]() )。また、
)。また、![]() の場合は
の場合は ![]() となることがわかる。
となることがわかる。
![]() で展開した多項式の形は
で展開した多項式の形は
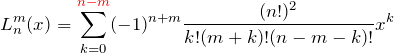
であり、![]() 次の多項式であることが確認できる。
次の多項式であることが確認できる。
ラゲール多項式の母関数の利用
![]() の母関数を利用すると、
の母関数を利用すると、
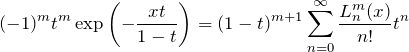
の関係を導くことができる。
ラゲール多項式の母関数
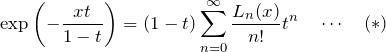
を
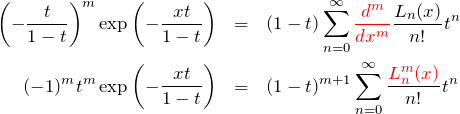
を得る。
内積の定義
![]() が満たす微分方程式
が満たす微分方程式
![]()
はステュルム-リウヴィル型微分方程式に分類される。その定義から内積と直交関係は
![]()
で表される(計量ベクトル空間)。![]() 、
、![]() は高々
は高々 ![]() 次と
次と ![]() 次の多項式であり、上の被積分関数にある
次の多項式であり、上の被積分関数にある ![]() により被積分関数は
により被積分関数は ![]() でも収束する。
でも収束する。
ラーゲル多項式との関係といくつかの便利な式
具体的な項については
![]()
を用いると良い。この表式は
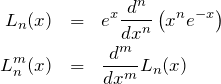
より得られる。また、式(*)の両辺を ![]() で微分して
で微分して
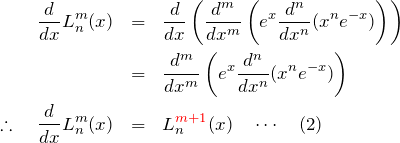
の関係がある。1回微分することで ![]() の陪多項式を作ることができる(
の陪多項式を作ることができる(![]() )。
)。
n=6までの具体的な項
以下では具体的な形を得るために式(2)を用いる。すなわち、![]() を計算したのち
を計算したのち ![]() 回微分して
回微分して ![]() を計算している。
を計算している。
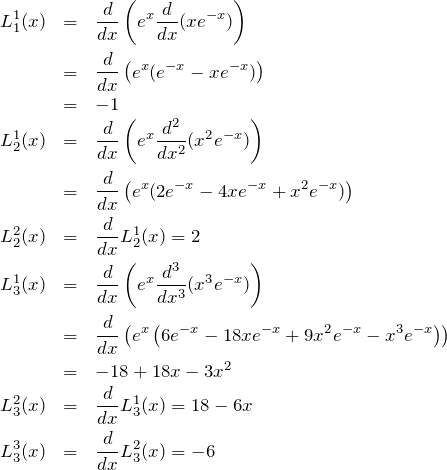
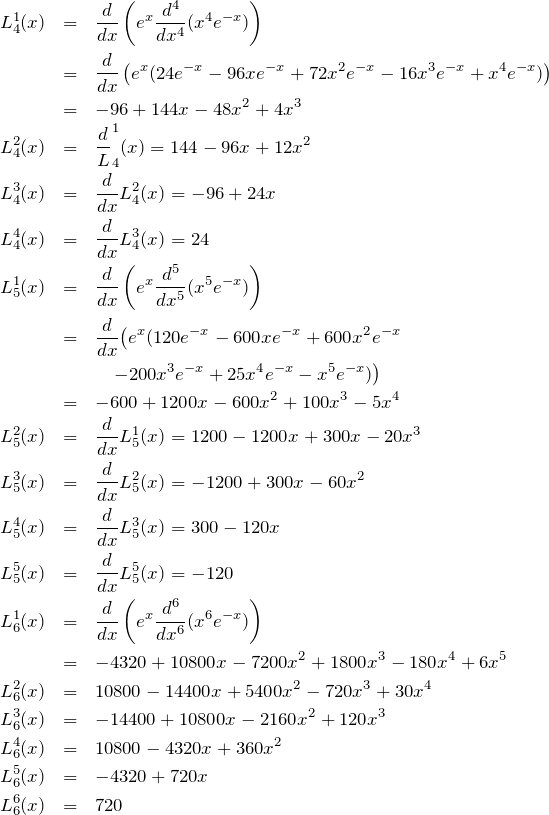
![]() を求めるときに使った式だけ下に載せておく。
を求めるときに使った式だけ下に載せておく。

ラゲール関数 Rnl(x)
定義
ラゲール関数 ![]() を以下のように定義する。
を以下のように定義する。
![]()
![]() は以下の微分方程式の解のひとつである。
は以下の微分方程式の解のひとつである。
![]()
内積とよく使う式
量子力学でよく使う式は下の通りである。
![]()
母関数で表した式を利用して証明を進めていけばよい。
上で見たラゲール陪多項式を母関数で表した式
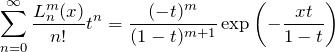
を使い、
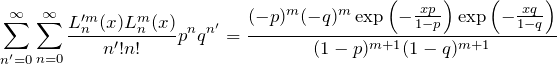
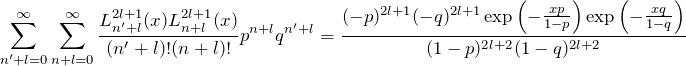
を得る。両辺に
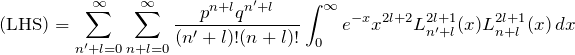
である。右辺(RHS)は
![]()
被積分関数の指数部分について
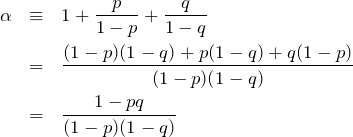
とおくと
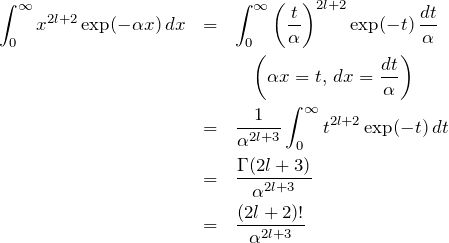
ここでガンマ関数
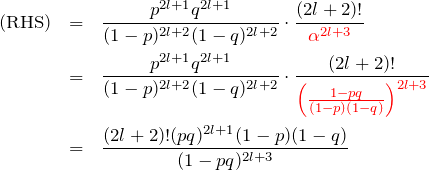
ここで、
![]()
を用いて(
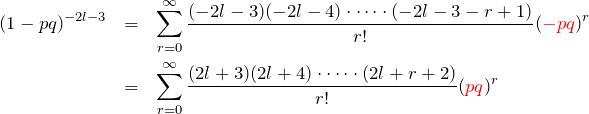
と展開できる。よって、
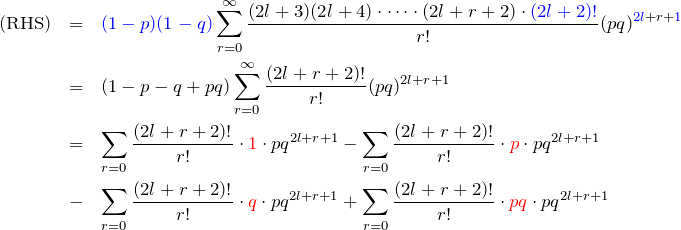
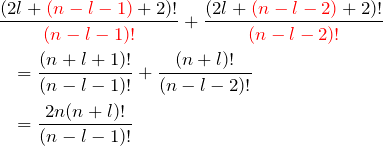
一方、(LHS)の
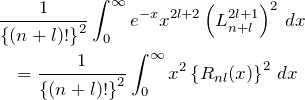
である。これより、
![]()
を得る。