ここでは、特性方程式を用いた2階同次線形微分方程式の一般解の導出と 基本例題を解いていく。 特性方程式の解が重解となる場合は除いた。はじめて微分方程式を解く人でも理解できるように説明する。
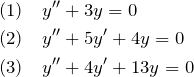
1. 一般解を求めよう
微分方程式を解くためには解の形をまず決めてしまうことである。 一般解の導出過程をより詳細に説明している。はじめて学習される人以外はスキップして「解き方流れまとめ」から見るのが良い。
一般解の導出
はじめて一般解を求めるひとのために説明しておく。
y(x)に関する2階同次線形微分方程式は次のような形をとる。
![]()
線形微分方程式を解くときに、まず
![]()
とおく。このように解の形を決めてしまうため、いま知りたいことは
「元の微分方程式を満たすような ![]() の値」
の値」
である。 元の微分方程式にこの形の ![]() を代入すると
を代入すると
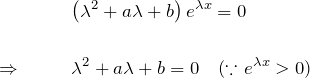
となる。これを「特性方程式」と呼ぶ。一般に ![]() 階同次微分方程式の特性方程式は
階同次微分方程式の特性方程式は ![]() 次方程式となる。
次方程式となる。
求めたい ![]() はこの二次方程式を解いて
はこの二次方程式を解いて
![]()
の2つとなる(解の公式)。例題を解くとわかるように、これらの解は複素数でも良い(重解の場合は少し違うためこちらで扱う)。以後の説明のため、解をそれぞれ
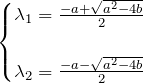
とおいておこう。
![]() が求められたため、はじめの解の形に代入してみる。仮に
が求められたため、はじめの解の形に代入してみる。仮に
(1) ![]()
![]()
となる(![]() は二次方程式の解であるため)。 このように求めた
は二次方程式の解であるため)。 このように求めた ![]() は確かに微分方程式を満たす。
は確かに微分方程式を満たす。
ここで、今の ![]() 定数
定数 ![]() 倍した
倍した
(2) ![]()
![]()
となり、微分方程式を満たす。
![]() についても同じく、定数を
についても同じく、定数を ![]() として
として
(3) ![]()
したがって、
![]()
もまた微分方程式を満たす。 このように定数倍した ![]() の足し算を 「線型結合」とよぶ。
の足し算を 「線型結合」とよぶ。
微分方程式の一般解はこのような線型結合で表す。
一般解・解き方まとめ
解法をまとめておこう。
-
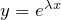 代入
代入 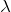 の二次方程式の解を
の二次方程式の解を 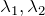 とする
とする- 解:
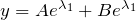 (A,Bは初期値で決まる定数)
(A,Bは初期値で決まる定数)
重要なポイントもまとめておこう。
2階同次線形微分方程式
![]()
![]()
![]()
2. 例題の解答
以下の ![]() は定数である。これらは微分方程式の初期値が与えられている場合に求めることができる。
は定数である。これらは微分方程式の初期値が与えられている場合に求めることができる。
例題(1)の解答
![]() を微分方程式へ代入して特性方程式
を微分方程式へ代入して特性方程式
![]()
を得る。この解は
![]()
である。
したがって、微分方程式の一般解は
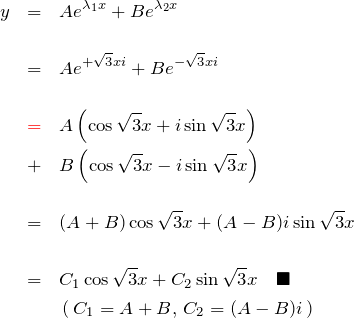
途中式で、以下のオイラーの公式を用いた
![]()
例題(2)の解答
![]() を微分方程式へ代入して特性方程式
を微分方程式へ代入して特性方程式
![]()
を得る。この解は
![]()
である。
したがって一般解は
![]()
*指数関数の肩が実数の場合はこのままでよい。複素数の場合は、(1)のようにオイラーの関係式を使うと三角関数で表すことができる。
**二次方程式の場合について、一方の解が複素数であればもう一方は、それと共役な複素数になる。 このことは方程式の解の形
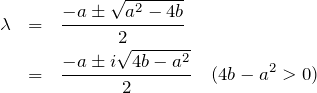
より明らかである。
例題(3)の解答
特性方程式は
![]()
であり、解は
![]()
である。
したがって一般解は
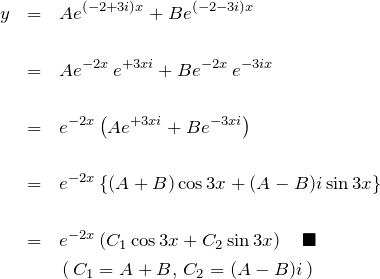
3. これらの微分方程式と解の意味
よく知られているように、高校物理で習うニュートンの運動方程式 もまた2階線形微分方程式である。ここで扱った4つの解のタイプは「ばねの振動運動」に関係するものを選んだ。 (1)は単振動、(2)は過減衰、(3)は減衰振動である。
詳細については、初期値を与えラプラス変換を用いて解いた こちらを参照されたい。
4. まとめ
2階同次線形微分方程式が解ければ ![]() 階同次線形微分方程式も解くことができる。 この次に学習する内容としては以下の2つであろう。
階同次線形微分方程式も解くことができる。 この次に学習する内容としては以下の2つであろう。
非同次系は特殊解を求める必要がある。この特殊解を求める作業は、場合によっては複雑になる。
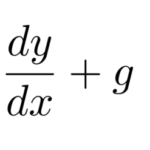
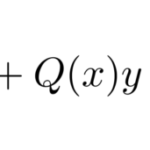
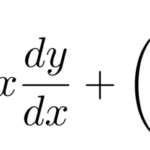
参考にさせていただきました。ありがとうございます。
しかし一つ疑問なのですが、オイラーの公式のsinθに虚数ⅰが抜けていませんでしょうか。
私の勘違いでしたらすみません。
ありがとうございます。iが抜け落ちていたので、修正しました。
混乱させてしまい申し訳ないです。