方向余弦は、あるベクトルの方向 を表す方法のひとつである。各軸から測った3つの角度で表現できる。ここでは絵を使って性質などをまとめておく。
学ぶこと
ベクトル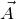 の方向を向く
の方向を向く - 3つの軸から測った角度
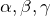 で表される
で表される -
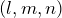 は単位ベクトル(大きさ1)になる
は単位ベクトル(大きさ1)になる
1. 方向余弦の表し方
表し方は図の通りである。
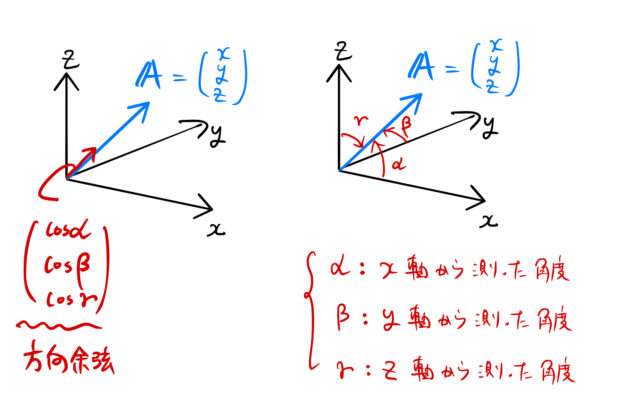
![]() の3つの余弦によって方向を表すので、「方向余弦」と呼ぶ。後の「3.角度の関係」に示すように
の3つの余弦によって方向を表すので、「方向余弦」と呼ぶ。後の「3.角度の関係」に示すように
![]()
の関係がある。
説明:
あるベクトル ![]() を考える。 このベクトルの方向は以下のように表すことができる。
を考える。 このベクトルの方向は以下のように表すことができる。
-
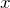 軸から測った角度
軸から測った角度 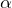
-
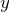 軸から測った角度
軸から測った角度 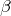
-
 軸から測った角度
軸から測った角度 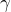
で表すことができる。つまり方向余弦を
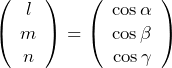
で表す。このベクトルの大きさは1である。
2. どうして cos になるか?
ベクトルの内積を使って示す。

説明: ![]() を
を
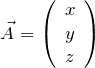
として、3つの軸から測ったときの角度をそれぞれ ![]() とする。このとき、3つの軸方向の単位ベクトル、
とする。このとき、3つの軸方向の単位ベクトル、
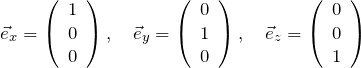
と![]() との内積をとる。
との内積をとる。
内積は ![]() を使った表現と成分で表現する2通りある。
を使った表現と成分で表現する2通りある。
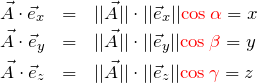
![]() とすると
とすると ![]() であるため
であるため
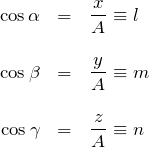
となる。方向余弦を表すために、![]() を用いると便利である。 (
を用いると便利である。 (![]() で表されているほうが意味は取りやすい気がするのだが。)
で表されているほうが意味は取りやすい気がするのだが。)
これより、![]() を方向余弦を使って表すことができる。
を方向余弦を使って表すことができる。
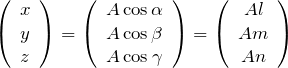
または
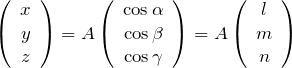
3. 角度の関係
最後に方向余弦
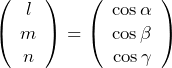
のベクトルの大きさが1であることを示す。すなわち、
![]()
を示す。

説明:
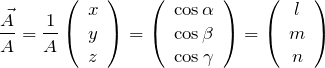
である。ベクトル ![]() を自分の大きさ
を自分の大きさ ![]() でわった左辺は単位ベクトルである。したがって、これらの等号で結ばれたベクトルの大きさはすべて1である。
でわった左辺は単位ベクトルである。したがって、これらの等号で結ばれたベクトルの大きさはすべて1である。
そういうわけで
![]()
あるいは
![]()
となる。
4. まとめ
方向余弦をまとめると以下のようになる。
- ベクトル
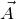 の方向を向く
の方向を向く - 3つの軸から測った角度
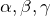 で表される
で表される -
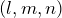 は単位ベクトル(大きさ1)になる
は単位ベクトル(大きさ1)になる
方向余弦を表す ![]() を導出するためには、各軸の単位ベクトルと内積を取ればよいことがわかる。
を導出するためには、各軸の単位ベクトルと内積を取ればよいことがわかる。
分かりやすく参考になりました。ありがとうございます。
(1章の最後と3章の冒頭のx,y,zの電子打ちの方向余弦に不要な2乗があるように思いました。)
すみません、助かります。修正いたしました。
ご指摘どうもありがとうございました。