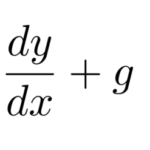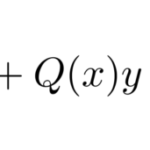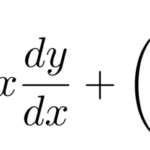一般的な2階同次線形微分方程式は特性方程式の解は異なる2つの解をもつため ![]() として一般解を求めることができる。ここでは、特性方程式の解が重解になるタイプの2階同次線形微分方程式を扱う。
として一般解を求めることができる。ここでは、特性方程式の解が重解になるタイプの2階同次線形微分方程式を扱う。
この微分方程式の一般解の導出過程と考え方をまとめ、 例題の解答をおこなう。基本解を求めるために「定数変化法」を用いているため、この方法についても説明する。
次の ![]() の
の ![]() に関する微分方程式を解け。
に関する微分方程式を解け。
![]()
1. 一般解を求める考え方
特性方程式の解が重解になる2階同次線形微分方程式
![]()
の一般解を考えていこう。
基本解について
まず微分方程式の基本解について説明しよう。
2階線形微分方程式の場合、特性方程式は2次方程式であり、 その解は複素数の範囲で2つある。これを ![]() として
として ![]() の2つが基本解である。
の2つが基本解である。
この微分方程式の一般解は基本解を2つ線型結合した
![]()
となる。
一般に、![]() 階微分方程式の場合は基本解は
階微分方程式の場合は基本解は ![]() 個あり、線型結合によって一般解をつくることができる。
個あり、線型結合によって一般解をつくることができる。
*補足:線型結合を行う場合には基底となる基本解が線形独立である必要がある。これは2つのベクトルの和で平面全体を構成するためには、2つのベクトルが平行であってはならないのと似ている。微分方程式の一般解も同様に、「独立な基本解」を用意する必要がある。微分方程式における基本解の独立性は、ロンスキー行列の行列式(ロンスキアン)が0でないことを調べれば良い(例題解答の終わりを参照)。
特性方程式の形
一般的な2階同次線形微分方程式と同じように ![]() を微分方程式へ代入して 特性方程式を作ると特性方程式の解が重解 (
を微分方程式へ代入して 特性方程式を作ると特性方程式の解が重解 (![]() )となる。 したがって、基本解として
)となる。 したがって、基本解として ![]() しか作れない(
しか作れない(![]() の2つの基本解が独立でないため)。
の2つの基本解が独立でないため)。
いま、2階線形微分方程式には2つの基本解のうちの1つ![]() しかない状態である。ここで残りの1つの基本解を求めるために次の「定数変化法」を用いる。
しかない状態である。ここで残りの1つの基本解を求めるために次の「定数変化法」を用いる。
定数変化法
定数変化法とは、1つ基本解の定数部分 ![]() を 関数
を 関数 ![]() として変化させてしまう方法である。
として変化させてしまう方法である。
基本解の定数 ![]() を 関数
を 関数 ![]() に変えて、
に変えて、![]() として
として ![]() を求める。これにより、もう1つの基本解を導く方法である。
を求める。これにより、もう1つの基本解を導く方法である。
言ってしまえば、残りの基本解を求める問題をすべて定数部分だった ![]() に押し込めた形になっている(定数→関数)。 本当にうまくいくかは
に押し込めた形になっている(定数→関数)。 本当にうまくいくかは ![]() を微分方程式に代入してみると分かる。
を微分方程式に代入してみると分かる。
まず、![]() を求める。
を求める。![]() に関する合成関数の微分であることに注意して計算する。
に関する合成関数の微分であることに注意して計算する。
![]()
これを元の微分方程式に代入して(項別に色付けした)
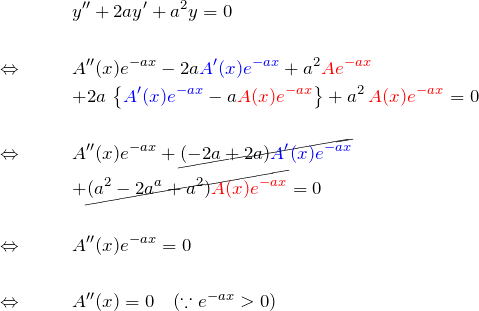
最後の行の ![]() に関する微分方程式は簡単に解けて、
に関する微分方程式は簡単に解けて、
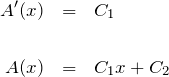
となる。ここで、![]() は定数である。
は定数である。
以上より、微分方程式 ![]() の一般解は
の一般解は
![]()
となる。
*一般解をみると、2つの基本解 ![]() は
は
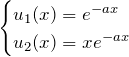
である。これらが独立であることは、ロンスキー行列の行列式(ロンスキアン)について
^2\\\\ &=&e^{-2ax}\neq 0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-cb92b32a898ac852b1685fc7135b3bcf_l3.png)
であることから分かる。
一般解・解き方まとめ
上記の結果をまとめておこう。
特性方程式が重解となる下のような2階微分方程式
![]()
![]()
2. 例題の解答
![]() について
について ![]() を代入すると、特性方程式は
を代入すると、特性方程式は
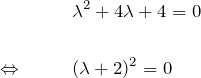
より ![]() の重解となる。
の重解となる。
したがって、微分方程式の一般解は
![]()
となる(![]() は初期値で決まる定数)。
は初期値で決まる定数)。
*この微分方程式の形は特性方程式の解が重解となる。 物理の問題でいうところの臨界振動の運動方程式として知られる。
3. まとめ
ここでは微分方程式を解く上で重要な「定数変化法」を学んだ。 定数変化法では、2階微分方程式について微分方程式の1つの基本解の定数部分を 「関数」とすることによって、もう1つの基本解を得る。
定数変化法は右辺に![]() などの項がある非同次線形微分方程式の場合でも 適用できるため、ここで基本を学んでおきたい。
などの項がある非同次線形微分方程式の場合でも 適用できるため、ここで基本を学んでおきたい。