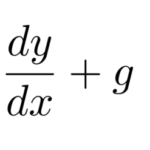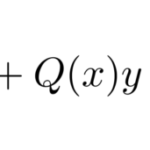定数係数の2階同次線形微分方程式がわかれば、定数係数の![]() 階微分方程式の一般解を求めることができる。 ここでは
階微分方程式の一般解を求めることができる。 ここでは
- パターン別に一般解を導出する
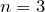 の微分方程式の例題を解く
の微分方程式の例題を解く
扱う例題は以下の通りである。
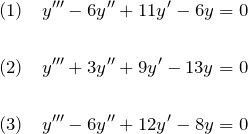
目次
1. 定数係数のn階同次線形微分方程式:一般解の導出
微分方程式へ ![]() を代入して特性方程式をつくる。
を代入して特性方程式をつくる。 ![]() 階線形微分方程式については
階線形微分方程式については
![]()
の ![]() 次方程式を得る。複素数の範囲で解は
次方程式を得る。複素数の範囲で解は ![]() 個ある。
個ある。![]() この解のうち
この解のうち ![]() 重解
重解 ![]() となる場合に注意する。
となる場合に注意する。
以下の3パターンについて一般解を見ていく。
- 特性方程式の解が異なる「n個の解」
- 特性方程式の解が「
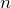 重解」
重解」 - 特性方程式の解が「m重解(m < n)」
特性方程式の解が異なる「n個の解」
![]() 個の解
個の解 ![]() の解がすべて異なる場合、 2階線形微分方程式と同様に 基本解
の解がすべて異なる場合、 2階線形微分方程式と同様に 基本解 ![]() を 線型結合すれば良い。
を 線型結合すれば良い。
![]()
*![]() 個の基本解の独立性:微分方程式の基本解が独立かどうかは、
ロンスキー行列の行列式(ロンスキアン)を調べれば良い。
今の場合のロンスキアンは、
個の基本解の独立性:微分方程式の基本解が独立かどうかは、
ロンスキー行列の行列式(ロンスキアン)を調べれば良い。
今の場合のロンスキアンは、
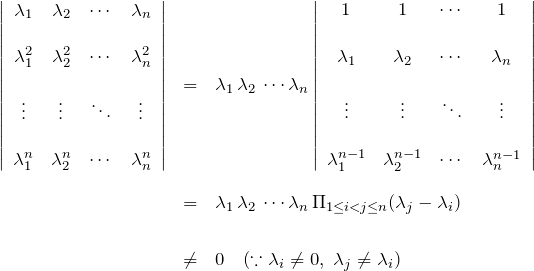
である。途中で行列式がヴァンデルモンドの行列式であることを利用した。 ロンスキアンが0ではないため、![]() 個の基本解は線型独立である。
個の基本解は線型独立である。
特性方程式の解が「n重解」
特性方程式の形が
![]()
であれば、![]() の
の ![]() 重解である。
重解である。
![]()
* このとき、![]() の基本解に対するロンスキアンは0にはならない(計算は略)。 したがって、
の基本解に対するロンスキアンは0にはならない(計算は略)。 したがって、![]() 個の基本解は独立である。
個の基本解は独立である。
この基本解の形は定数変化法により求めることができる。
たとえば ![]() のときを考える。微分方程式
のときを考える。微分方程式
![]()
の特性方程式
![]()
に対して、![]() の三重解である。
の三重解である。
基本解のひとつを ![]() とおく。ここで「定数変化法」により、 定数
とおく。ここで「定数変化法」により、 定数 ![]() も
も ![]() の関数と改める。この
の関数と改める。この ![]() に対して合成関数の微分をおこなう。
に対して合成関数の微分をおこなう。
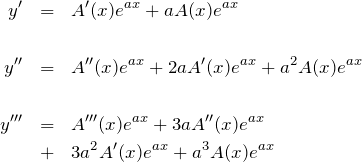
これらを元の微分方程式に代入して整理すると
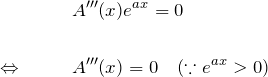
となる。したがって ![]() は二次関数で
定数
は二次関数で
定数 ![]() を用いて
を用いて
![]()
となる。これを ![]() に代入して
一般解
に代入して
一般解
![]()
を得る。
特性方程式の解が「m重解(m<n)」
特性方程式の ![]() 個の解のうち、
個の解のうち、 ![]() 重解
重解 ![]() がある場合を考える。また残りの
がある場合を考える。また残りの ![]() 個については異なる解の場合を考える。
個については異なる解の場合を考える。
このとき特性方程式の形は
![]()
である。
![]() 個の基本解
個の基本解 ![]() は互いに独立で
は互いに独立で ![]() とも独立である。 したがって
とも独立である。 したがって ![]() に対して独立な基本解を作ると、
に対して独立な基本解を作ると、
![]()
を得る(![]() 重解の場合を参照)。 これら
重解の場合を参照)。 これら ![]() 個の基本解と
個の基本解と ![]() 個の基本解を線型結合して一般解を得る。
個の基本解を線型結合して一般解を得る。
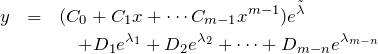
2.例題の解答
以下 ![]() は初期値によって決まる定数である。
は初期値によって決まる定数である。
例題(1)の解答
【3個の異なる実数解の場合】
特性方程式は
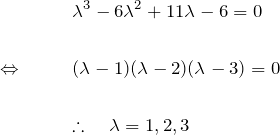
したがって一般解は
![]()
となる。
例題(2)の解答
【![]() が虚数となる場合】
が虚数となる場合】
特性方程式は
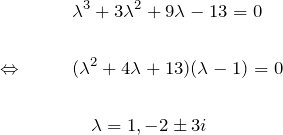
となる(1つの実数解と2つの互いに共役な虚数解)。
したがって一般解
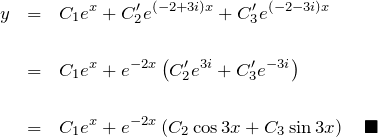
となる。ここで、![]() の定数である。
の定数である。
*最後の行でオイラーの関係式
![]()
を用いた。
**2つの虚数解が共役なので指数関数は三角関数で綺麗に表すことができる。
例題(3)の解答
【三重解型】 特性方程式は
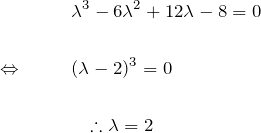
となる(三重解)。 したがって一般解は
![]()
となる。
3.まとめ
定数係数の ![]() 階同次線形微分方程式でも、2階の場合と解き方はあまり変わっていない。 結局のところ、独立な基本解を求めて線型結合すれば良いということがわかる。 また独立な基本解を求める場合には、特性方程式の解が
階同次線形微分方程式でも、2階の場合と解き方はあまり変わっていない。 結局のところ、独立な基本解を求めて線型結合すれば良いということがわかる。 また独立な基本解を求める場合には、特性方程式の解が ![]() 重解になっているかを調べる必要があった。
重解になっているかを調べる必要があった。