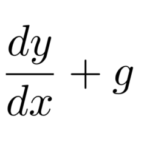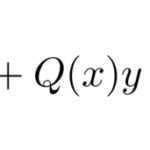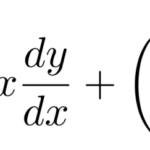同次線形微分方程式(2階)は
![]()
のような右辺が0の線形微分方程式である(解き方)。 ここではその右辺が ![]() の関数となった
の関数となった
![]()
で表される非同次線形微分方程式を扱う。さらに線形微分方程式の構造から、重要な概念である一般解と特殊解についてまとめておこう。
ここでは最も簡単な ![]() が「定数係数」の問題を扱う。 この微分方程式の解法は具体的な例題を解いて定着させていきたい。
が「定数係数」の問題を扱う。 この微分方程式の解法は具体的な例題を解いて定着させていきたい。
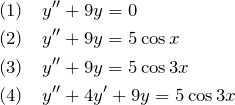
目次
1. 非同次線形微分方程式
非同次微分方程式とは?
冒頭で説明した通り「非同次」の微分方程式とは
![]()
の形をもつ。非同次型の微分方程式を解くためには、同次型の
![]()
を解けることが前提である。これは ![]() 階微分方程式の場合でも同様である。
階微分方程式の場合でも同様である。
非同次型の「解き方」はこれだけ
結論から言うと、非同次型の一般解は
![]()
で表される。ここで、![]() は余関数、
は余関数、![]() は特殊解であり、このことは後で説明する。
は特殊解であり、このことは後で説明する。
一般解が上の形になっているため、非同次線形微分方程式の解き方は
- 右辺を0として同次型の微分方程式を解いて余関数を求める
- 右辺が
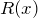 となる特殊解を探す
となる特殊解を探す - 2つの結果を足す
だけである。以下ではこのように求められる理由を書いていく。
なぜ一般解(余関数)と特殊解に分けた?
まず用語を整理しておこう。
- 一般解:同次型(右辺ゼロ)を満たす
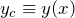 のこと
のこと - 特殊解:非同次型で、左辺を計算したら右辺
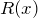 になる
になる 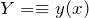 のこと
のこと - 余関数:非同次型における
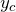 のこと
のこと
非同次線形微分方程式を求めるときに、なぜ余関数と特殊解に分けることができるのだろうか。その理由は非同次型の微分方程式の構造にある。
たとえば例題(2)では、
![]()
と書ける。したがって、「1の余関数を求める式」と「2の特殊解を求める式」に分けることができる。
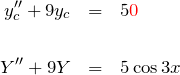
この結果を用いて、微分方程式が線形である場合は ![]() とすればよい。 そういうわけで、非同次線形微分方程式では余関数(同次型の一般解)と特殊解に分けて求めているのである。
とすればよい。 そういうわけで、非同次線形微分方程式では余関数(同次型の一般解)と特殊解に分けて求めているのである。
以下では「未定係数法」による特殊解の求め方を見ていこう。
【特殊解の求め方(未定係数法)】そのままの形が使える
特殊解を求めるため例題(2)を見てみる。
![]()
やること:右辺が ![]() になる
になる ![]() を「勘」で探す
を「勘」で探す
勘と言えども目星は付くと思う。 ![]() ,
, ![]() などは明らかに違うことがわかる。ここでは右辺の三角関数の形に合わせた
などは明らかに違うことがわかる。ここでは右辺の三角関数の形に合わせた ![]() を考えるのがよい。
を考えるのがよい。
特殊解の目星:![]()
あとはこの定数 ![]() を求めるだけである。「目星」を左辺へ代入しよう。 各項について縦にならべると見やすいし、計算ミスも防げるだろう。
を求めるだけである。「目星」を左辺へ代入しよう。 各項について縦にならべると見やすいし、計算ミスも防げるだろう。
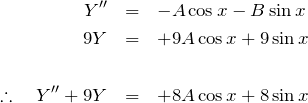
これが左辺の ![]() と等しくなるため、
と等しくなるため、 ![]() である。
これで特殊解
である。
これで特殊解 ![]() を求めることができた。
を求めることができた。
![]()
このように特殊解の形の目星を立てて、係数を求めていけば良い。
【特殊解の求め方(未定係数法)】そのままの形が使えない
上記の「目星」は例題(2)では困らないが、例題(3)では困る。例題(3)を見てみる。
![]()
同じように右辺の ![]() に合わせて
に合わせて
特殊解の目星:![]()
としてみる。このとき微分方程式の左辺は、
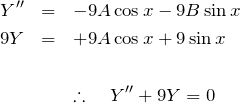
となる。消えてしまう。この原因は今考えている ![]() の形がそのまま同次形の
の形がそのまま同次形の
![]()
の一般解になっているからである。
この場合は新たに特殊解の形を考えなくてはならない。しかし、![]() や
や ![]() のような形ではないことは明らかだろう。もっと単純な関数で表すべきである。以下のように。
のような形ではないことは明らかだろう。もっと単純な関数で表すべきである。以下のように。
特殊解の目星:![]()
この形で微分方程式の左辺を計算してみる。
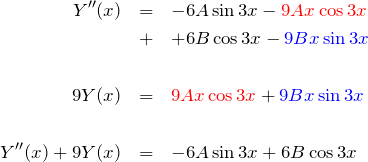
となる。これを右辺の ![]() と比較すると
と比較すると ![]() を得る。
を得る。
したがって特殊解は
![]()
となる。
特殊解の形を見極める
上で困った問題は、同次形の特性方程式の解 ![]() が、右辺において
が、右辺において ![]() などの形になっている場合におこる。例として以下のような非同次微分方程式が挙げられる(特性方程式の解も示しておく)。
などの形になっている場合におこる。例として以下のような非同次微分方程式が挙げられる(特性方程式の解も示しておく)。
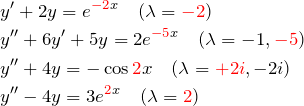
それぞれ特殊解の形は
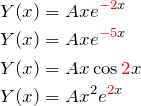
4つめについては重解であるため、![]() についてより高次の特殊解が必要となる。 実際に、
についてより高次の特殊解が必要となる。 実際に、![]() ではうまくいかない(各自確認)。 もちろん3重解となっている場合は
ではうまくいかない(各自確認)。 もちろん3重解となっている場合は ![]() と置かなくてはならない。
と置かなくてはならない。
2. 解答
以下 ![]() は初期値で決まる定数とする。
は初期値で決まる定数とする。
例題(1)の解答
この問題の一般解は例題(2)(3)の余関数 ![]() に共通して対応する。
に共通して対応する。
【解答】 ![]() として特性方程式を作ると
として特性方程式を作ると
![]()
したがって一般解は
![]()
以下の解答(2)(3)では余関数 ![]() とする。
とする。
例題(2)の解答
特殊解 ![]() の詳しい求め方は項目1を参考にされたい。
の詳しい求め方は項目1を参考にされたい。
【解答】 余関数は(1)の ![]() で与えられる。また、特殊解を
で与えられる。また、特殊解を
![]()
と置いて左辺を計算する。
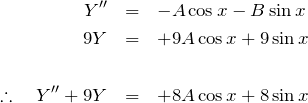
したがって、![]() となる。 よって微分方程式の解は
となる。 よって微分方程式の解は
![]()
例題(3)の解答
特殊解 ![]() の詳しい求め方は項目1を参考にされたい。 【解答】 余関数は(1)の
の詳しい求め方は項目1を参考にされたい。 【解答】 余関数は(1)の ![]() で与えられる。また、特殊解を
で与えられる。また、特殊解を
![]()
と置いて左辺を計算する。
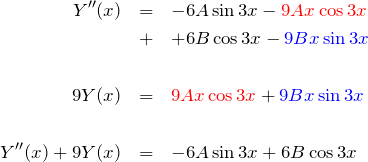
したがって、![]() となる。よって微分方程式の解は
となる。よって微分方程式の解は
![]()
例題(4)の解答
【解答】
![]() として特性方程式を作ると
として特性方程式を作ると
![]()
となる。したがって余関数 ![]() は
は
![]()
ここで特殊解の形を
![]()
と置いて微分方程式の左辺を計算する。
微分したものをそれぞれ並べると
![]()
である。微分方程式の係数倍して、左辺を計算すると
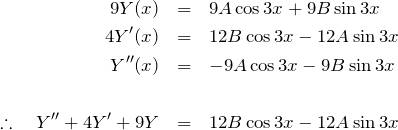
となる。したがって、![]() である。
である。
以上より微分方程式の解を求めることができる。
![]()
3. まとめ
非同次線形微分方程式の解く方法は
- 余関数を求める
- 特殊解を求める
であった。余関数を求めるためには同次線形型の微分方程式が解けないといけない。また、特殊解を求めるためには特殊解の形を推測することが必要であった。
ここで扱った微分方程式に初期値を与えると、ラプラス変換でも解ける(実際に解いたもの)。微分方程式にはいろいろな解き方があり、ここで扱った「未定係数法」もその1つである。 次の項では「定数変化法」で同じ問題を解いていきたい。