全記事一覧 > 数学 > 微分方程式

【Green関数】微分方程式を解くための道具／Green関数の簡単な意味（基礎）

　誰でも初学者のうち（人生初見プレイ）は、 物理で「えぇ…習ってない…知らない…」といった数学が たくさん出てくるので逐一学習しなくてはいけない。このGreen関数もその代表的なものであろう。

　ここでは微分方程式を解くためのGreen関数の基礎をまとめよう。物理でGreen関数を使うための導入として読んでもらいたい。

　具体的に物理で一番初めに出会う場面は、電磁気学のポアソン方程式を解いて スカラーポテンシャル \phi を求めるところかもしれない。したがって、最後にポアソンを例にGreen関数の意味やらイメージやらを簡単にまとめておく。


1. Green関数の簡単な話

　微分方程式におけるGreen関数法では、微分方程式の解に対応するGreen関数を求めることで元々の微分方程式の解を得る。この魔法のような方法について、その構造を説明していこう。


微分方程式を直接解く代わりに

　例として１変数 x に関する微分方程式を考える。

    \begin{eqnarray*} {\mathcal D} f(x)=h(x) \quad\cdots\quad (*) \end{eqnarray*}

　h(x) は既知の関数であり、求めたい関数は f(x) である。 また {\mathcal D} は x に作用する演算子である。 以下ではわかりやすく {\mathcal D}_x と書いておく。次のようなポアソン方程式においては {\mathcal D}=\nabla^2 である。

    \begin{eqnarray*} \nabla^2 f({\bf r})=h({\bf r}) \end{eqnarray*}


　次に何故そうなるかは一旦置いておいて、 Green関数が満たすべき方程式を作ろう。

    \begin{eqnarray*} {\mathcal D_x} G(x-x')=\delta(x-x') \quad\cdots\quad (*)' \end{eqnarray*}

　演算子はそのまま x に対して作用する。また右辺をデルタ関数に置き換え f(x)\rightarrow G(x-x') とした。この G(x-x') をGreen関数と呼ぶ。 後で説明するように、式(*)を解いて f(x) を求める代わりに G(x-x') を求めれば良い。 したがって、この瞬間に解くべき問題は変わってしまったのである！

ポイント

(*)のf(x)を求める → (*)’のG(x-x') を求める


*ここでは最も簡単な時間に依存せず位置だけに依存するGreen関数 G(x,x') を考えた。 時間に依存する G(x,t; x',t') もある。さらにここでは、x と x' の２点間距離のみに依存する G(x-x') を考えている。


なぜGreen関数を求めれば良いのか

　煙に巻かれたようである。では、G(x-x') を求めれば、f(x) がわかる仕組みを説明しよう。

　その理由は

    \begin{eqnarray*} f(x)=\int \textcolor{red}{G(x-x')} h(x') dx'\quad\cdots\quad (*)'' \end{eqnarray*}

　とすれば元の微分方程式の解 f(x) を作れるからである。被積分関数は既知であり、積分範囲は空間全体にとる。


　実際に f(x) が微分方程式の解になっているかどうかは(*)に代入してみればわかる。 このとき演算子 {\mathcal D} は x にのみ作用し、 h(x') のような x' の関数には作用しないことに注意する。

(*)の左辺：

    \begin{eqnarray*} {\mathcal D}_x f(x) &=&{\mathcal D}_x \left[\int G(x-x') h(x') dx'\right]\\\\ &=&\int \textcolor{red}{{\mathcal D}_x G(x-x')} h(x') dx'\\\\ &=&\int \textcolor{red}{\delta(x-x')}h(x')dx'\quad(\because {\rm Eq.}(*))\\\\ &=&h(x)\quad\blacksquare \end{eqnarray*}

となり、確かに微分方程式の右辺に一致する。最後の行では以下のデルタ関数の定義を使った。

    \begin{eqnarray*} \int_{-\infty}^{\infty} f(x) \delta(x-a)\,dx=f(a) \end{eqnarray*}


以上のように G(x-x') を求めることで、微分方程式の解 f(x) を求められたことになる。


ポイント

微分方程式を解いて f(x) を求めるためには、 Green関数を求めて以下の積分を実行すればよい。

    \begin{eqnarray*} f(x)=\int G(x-x') h(x') dx'\end{eqnarray*}



Green関数のイメージ

　簡単にそのイメージを説明しておく。

　Green関数の形は、もとの微分方程式の形によって様々であるため、 具体的な式があるほうがわかりやすい。 したがって、次のスカラーポテンシャルに関するポアソン方程式を元の微分方程式として説明する。

    \begin{eqnarray*} \nabla^2 \phi({\bf r}) =-\frac{\rho({\bf r})}{\varepsilon} \end{eqnarray*}

スカラーポテンシャルというカタカナが苦手なら、\phi({\bf r}) はおおよそ電位のようなものと思えばよいだろう（電場 {\bf E({\bf r})}=\nabla\phi({\bf r}) だから E=V/d と似ている）。


　上のポアソン方程式から既にGreen関数を求まっているところからスタートしよう。 微分方程式の解は

    \begin{eqnarray*} \phi({\bf r})&=&\int G({\bf r}-{\bf r}') \left(-\frac{\rho({\bf r'})}{\varepsilon}\right)\,d{\bf r}' \end{eqnarray*}

となる。


　この式の意味を見るためまず、 ２つの位置ベクトル {\bf r} と {\bf r}' の意味を整理しておこう。 {\bf r} は 求めたい \phi({\bf r}) の位置を表している。 また {\bf r}' はその位置にある電荷密度 \rho({\bf r}') を指定するベクトルである。

　次に、積分のイメージを思い出そう。積分は細かく区切って足し合わせることであった。 そうすると {\bf r}' の積分の意味が見えてくるだろう。 つまり上の積分は、位置 {\bf r}' にある電荷が {\bf r} に作るスカラーポテンシャルを、足し合わせて集めているのである。


　そうすると足し合わせる前の被積分関数

    \begin{eqnarray*} G({\bf r}-{\bf r}')\left(-\frac{\rho({\bf r}')}{\varepsilon}\right) \end{eqnarray*}

は、位置 {\bf r}' の電荷 \rho({\bf r}') が {\bf r} に作るスカラーポテンシャルを表す。


ここまで分かれば、G({\bf r}-{\bf r}') が {\bf r} と {\bf r}' の２変数（の差）で表されている理由もわかるだろう。

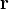  • {\bf r}： ポテンシャルが作られる場所
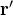  • {\bf r}'：ポテンシャルを作る元になる場所（電荷の位置）

であるため、ここでの G({\bf r}-{\bf r}') は空間の伝わり方（伝播）を表している関数と言える。この場合、Green関数が記述するのは、電荷密度を誘電率で除した \rho/\varepsilon がどのようにスカラーポテンシャルを作るかということである。これがGreen関数のおおまか意味である。


*「伝わり方」と「伝わりやすさ」 \varepsilon は電場の伝わりやすさの程度のようなもの。 真空の \varepsilon_0 と考えれば真空中での場の伝わりやすさになる。 例えば、点電荷が作るポテンシャルは点電荷の中心 {\bf r}'=0 からの距離に反比例する。

    \begin{eqnarray*} \phi({\bf r})\propto \frac{1}{|{\bf r}|} \end{eqnarray*}

空間が等方的であれば、\varepsilon によらず距離に反比例して伝わるであろう。 この1/|{\bf r}| が「伝わり方」に対応して、誘電率は「伝わりやすさ」に対応する。


2. まとめ

　ざっくり書いてしまって良いものかと思ったが、Green関数の導入としてイメージだけ伝われば良いとして書いた。

　ここではGreen関数の求め方は扱わなかった。したがって、これを読んだだけではポアソン方程式は解けない。そりゃそうだ。f(x) を求める代わりに G(x-x') を求めれば良いと言っておいて、G(x-x') を求めていないのだから。

　ということで、次は件のGreen関数を求める方法を学ばなくてはならないだろう。

おわり。



2件のコメント

  1. 匿名

    今、境界要素法について勉強してるところです。そこで基本解の話が出てきまして、これって何？と考えて検索しておりました。そこで、green関数にたどり着いた次第です。
    説明を読ませて頂き目から鱗が落ちた感じです。大変良く理解できました。
    ありがとうございました。

    返信
    • batapara

      コメントありがとうございます。
      急に出てくるからびっくりするんですよね。
      境界条件があると複雑になると思いますが、今回は基本的なイメージというところで説明させていただきました。

      返信

コメントを残す

メールアドレスが公開されることはありません。