以下のガウスの発散定理は、マクスウェル方程式の微分型「ガウスの法則」を導出するときに使われる。この発散定理のざっくりとした理解は、
「面積分(左辺)と体積積分(右辺)をつなげる」
ということである。 ここではわかりやすく証明していこうと思う。
![]()
目次
1. 発散(div)の復習
ベクトル発散の表現
発散はベクトルとベクトルの内積で表される。したがって発散はスカラー量である。 復習すると定義は以下のようになる。ベクトル ![]() とナブラ演算子
とナブラ演算子 ![]() について
について
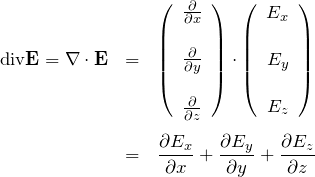
ベクトルの発散の簡単なイメージ
div のイメージは湧き出しである。 ある考えている点から
「どのくらいのベクトル量が流れ出ているか」
を調べる。この値がマイナスであればベクトルの流入を表す。
電磁気学の場合、このベクトル量は電気力線や磁力線(電場 ![]() や磁場
や磁場 ![]() )である。
)である。
考えている点で ![]() であれば、電気力線が湧き出していることを意味する。
であれば、電気力線が湧き出していることを意味する。![]() であれば、電気力線が吸い込まれていることを意味する。 おおよそ、蛇口から流れ出る水と排水口に吸い込まれる水のようなイメージを持てば良い。
であれば、電気力線が吸い込まれていることを意味する。 おおよそ、蛇口から流れ出る水と排水口に吸い込まれる水のようなイメージを持てば良い。
2. ガウスの発散定理の証明
以下では向きと大きさをもったベクトル量として電場 ![]() で考えよう。 これは電気力線のようなイメージで考えてもらっても良い。
で考えよう。 これは電気力線のようなイメージで考えてもらっても良い。
証明の流れ
証明は以下の考え方で進める。
- 考えている領域を細かく区切る(微小領域)
- 立方体の「微小領域」の6面のうち平行な2面について流出を調べる
- 残りの2組の2面についても同様に調べる
- 「微小領域」を足し合わせて、もとの領域に戻す
このように、「細かく区切って、微小領域内で発散を調べて、足し合わせる」(積分)ことで証明を進めていく。
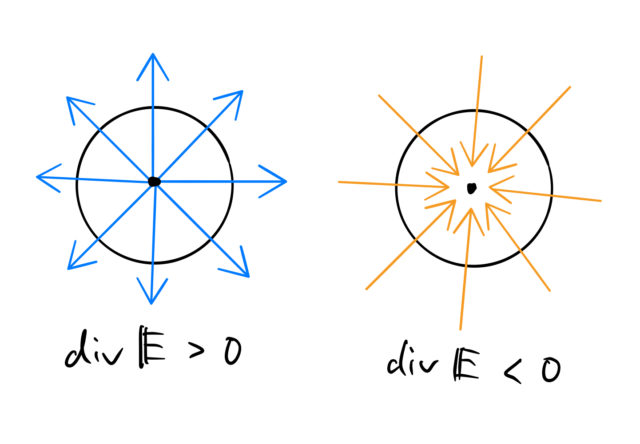
ガウスの発散定理の証明
図に示したような任意の領域を考える。この領域の表面積を ![]() 、体積を
、体積を ![]() とする。
とする。
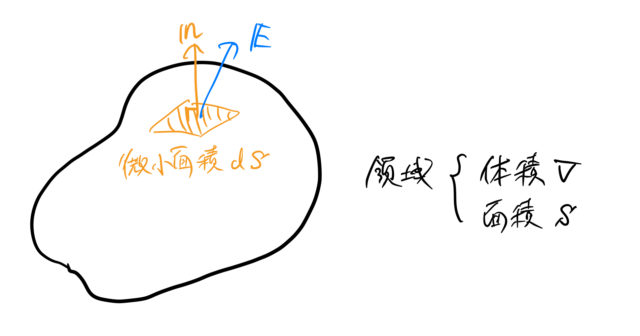
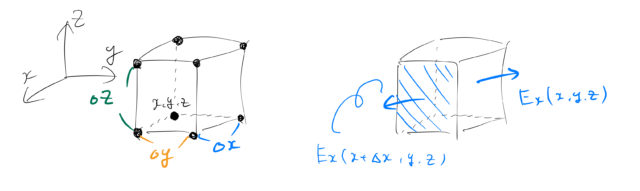
1. 細かく区切る
この領域を立方体に「みじん切り」にする。 絵では有限の大きさで区切っているが、無限に細かく切れば「端」も綺麗にくぎれる。
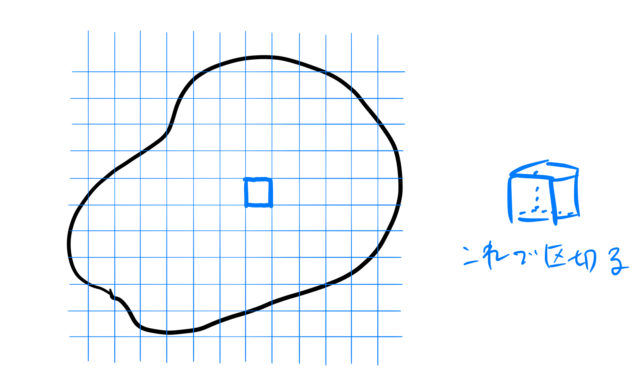
区切ったうち、1つの立方体について考えてみる。この立方体の6面から流出するベクトルを調べたい
このときベクトル ![]() の向きはすべて「外向き」としよう。 実際には
の向きはすべて「外向き」としよう。 実際には ![]() 軸方向にマイナスの向きに流れている可能性もあるが、 最終的な結果にそれは含まれる(符号は後からついてくる)。
軸方向にマイナスの向きに流れている可能性もあるが、 最終的な結果にそれは含まれる(符号は後からついてくる)。
2. x と x+Δx にある2面の流出
2つの面におけるベクトルの流出量は
- 前の面:
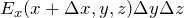 (
(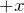 方向)
方向) - 奥の面:
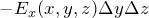 (
(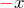 方向)
方向)
である。ここで、![]() は
は ![]() の
の ![]() 成分 (
成分 (![]() 方向のベクトルの大きさ)である。
方向のベクトルの大きさ)である。
考えている面でそれぞれの値は変わらないとする。 これより立方体から流出する量については、上の2つのベクトルの大きさをそれぞれ ![]() 面の面積(
面の面積( ![]() )倍する必要がある。 したがって、
)倍する必要がある。 したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Delta E_x \Delta y\Delta z&=& \textcolor{red}{E_x(x+\Delta, y,z)} - E_x(x,y,z)\\\\ &\simeq&\left[\textcolor{red}{E_x(x,y,z)+\frac{\partial E_x(x,y,z)}{\partial x}\,\Delta x} -E_x(x,y,z)\right] \Delta y \Delta z\\\\ &=& \frac{\partial E_x(x,y,z)}{\partial x}\, \textcolor{blue}{\Delta x \Delta y \Delta z}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-c13362295f987cc336f0251dee89ed5f_l3.png)
![]() の形をつくるのがコツである。ここで、赤色部分では
の形をつくるのがコツである。ここで、赤色部分では ![]() 点周りテイラー展開
点周りテイラー展開![]() を用いて1次の項までとった。
を用いて1次の項までとった。 ![]() の2次より高次の項については、
の2次より高次の項については、![]() が微小量なので無視できる。
が微小量なので無視できる。
「ガウスの発散定理」の証明に限らず、微小領域を用いて何か定理や式を証明する場合には、関数をテイラー展開することが多い。したがって、微分積分はしっかりやっておく。
3. 残りの2組の2面について
![]() と
と ![]() 面について立方体からの流出は、
面について立方体からの流出は、 ![]() 方向と同様に
方向と同様に
![]()
![]() と
と ![]() 面についても同様に、
面についても同様に、
![]()
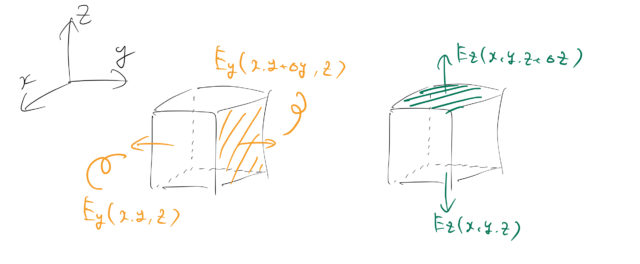
これより、立方体の微小領域から流出する電場ベクトルの量(スカラー)は
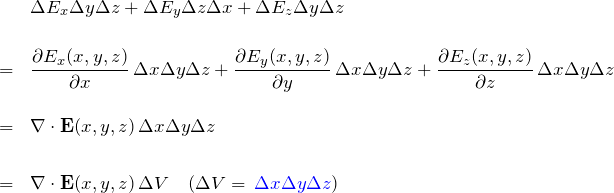
最後の行の ![]() は立方体の微小体積を表す。また、左辺は立方体の各面からの流出(マイナスなら流入)を表している。
は立方体の微小体積を表す。また、左辺は立方体の各面からの流出(マイナスなら流入)を表している。
4. 「微小領域」を足し合わせる
みじん切りにした領域(立方体)を集めて元の領域に戻す。それぞれの立方体に番号 ![]() をつけて足し合わせよう。
をつけて足し合わせよう。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\sum_i \left[\Delta E_{x}(x_i,y_i,z_i) \Delta y\Delta z+ \Delta E_{y}(x_i,y_i,z_i) \Delta z\Delta x+ \Delta E_{z}(x_i,y_i,z_i) \Delta y\Delta z\right] \\\\ \quad &=& \sum_i \nabla_i \cdot {\bf E}(x_i,y_i,z_i) \,\Delta V_i \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9fb66e06e527e9e7ee1a37e56c84a205_l3.png)
ここで、![]() は
は ![]() 番目の立方体の座標を表し、
番目の立方体の座標を表し、![]() は
は ![]() 番目の立方体の
番目の立方体の ![]() 面から
面から ![]() 方向に流出する電場の大きさを表す。
方向に流出する電場の大きさを表す。![]() は
は ![]() に対して
に対して ![]() をとることを表す。
をとることを表す。
右辺(RHS; right-hand side)について、無限小にすると ![]() となり、
となり、![]() は積分に置き換わる。
は積分に置き換わる。
![]()
次に左辺(LHS; left-hand side)について、図のように全体を細かく区切った状況を考えよう。このとき、隣の微小領域と重なる部分はベクトルが反対方向に向いているはずである。つまり、全体を足し合わせたときに、重なる部分に現れる2つのベクトルの和は0になる。
このことから、総和をとったときに残るのは微小領域が重ならない「端」である。この端の全面積は、いま考えている全体の領域の表面積にあたる。
また、これまで考えてきたベクトルはすべて面に垂直な方向にあった。 これを表現するために面に垂直な単位法線ベクトル ![]() 導入する。微小面の面積を
導入する。微小面の面積を ![]() とすれば、 計算に必要な電場ベクトルの大きさは、
とすれば、 計算に必要な電場ベクトルの大きさは、 ![]() あたり
あたり ![]() である。これを全領域の表面積だけ集めれば良い(
である。これを全領域の表面積だけ集めれば良い(![]() で積分する)。
で積分する)。
*電場ベクトルと単位法線ベクトルの内積をとれば、電場の法線ベクトル方向の成分を得る。(【参考】ベクトルの内積/射影の意味)
以上より、
![]()
これで「ガウスの発散定理」を得ることができた。 この定理と積分型ガウスの法則により、微分型ガウスの法則を導出することができる。 微分型についてはマクスウェル方程式の中にあり、
![]()
として知られている。
3. まとめ
ここでは、発散(div)についての簡単な説明と、「ガウスの発散定理」を証明してきた。 ここで扱った内容を用いて、微分型ガウスの法則を導くことができる。 マクスウェル方程式の重要な式の1つであるため、 ガウスの発散定理とともに押さえておきたい。
[1] テイラー展開について:
![]() まわりの展開を考える。1変数の場合のテイラー展開は
まわりの展開を考える。1変数の場合のテイラー展開は
![]()
である。多変数の場合については、考えている変数以外は固定して同様に展開すれば良い。
![]()
となる。
ありがとうございます
素晴らしい。。。。
マジで感動しました。
他のサイトが式をメインでC級関数が、、、グリーンの、、
などと述べているところ具体的に図解しわかりやすい言葉で表現できるその技量に感服いたしました。
ありがとうございます。
ありがとうございます。
図を多めにするコンセプトで記事を作って、教科書内容を補完できるようにしています。
お役に立てて良かったです。