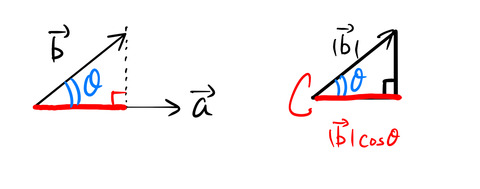ベクトルにおける内積は単なる成分計算ではない。そのことを絵を使って知ってもらいたい。なんとなくのイメージでいいので知っておくと良いだろう。また、大学数学を学ぼうとする方は、内積の話が線型空間やフーリエ解析などの多くの単元で現れていることに気づくだろう。
目次
1. ベクトル内積
平面ベクトル ![]() と
と ![]() の内積を考えよう。ベクトルは向きと大きさを持っていることに注意する。
の内積を考えよう。ベクトルは向きと大きさを持っていることに注意する。
1.1 定義
2つのベクトルの内積は ![]() によって表すことができる。
によって表すことができる。
![]()
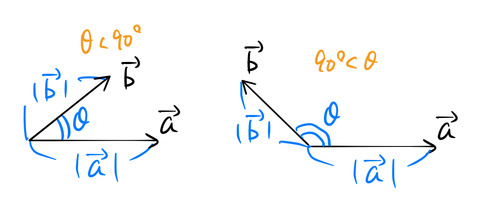
なす角度 ![]() は 0°から180°までで定義される。 図では90°より大きい
は 0°から180°までで定義される。 図では90°より大きい ![]() と90°より小さい
と90°より小さい![]() の場合を描いた。どちらの場合も使う式は同じである。
の場合を描いた。どちらの場合も使う式は同じである。
1.2 射影をみる
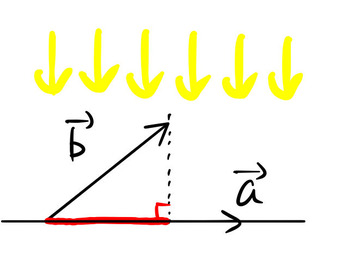
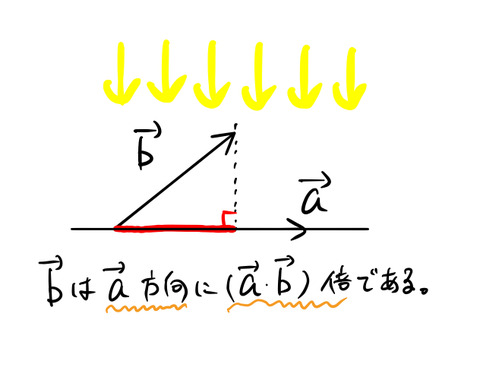
よく内積では「射影」という言葉が使われる。図は、![]() に垂直な方向から光を当てたときの様子を描いた。
に垂直な方向から光を当てたときの様子を描いた。
![]() の影になる部分が射影と呼ばれるものである。絵では射影は赤色の線に対応する。これを見れば「なぜ内積の定義に
の影になる部分が射影と呼ばれるものである。絵では射影は赤色の線に対応する。これを見れば「なぜ内積の定義に ![]() が現れるか」がわかるだろう。つまり、下の絵を見て欲しい。
が現れるか」がわかるだろう。つまり、下の絵を見て欲しい。
赤い射影の部分は、![]() の大きさのを
の大きさのを ![]() で表したものになる。つまり、赤線の長さは
で表したものになる。つまり、赤線の長さは ![]() である。
である。
1.3 それは何を意味する?
こんな内積なんて定義して何がうれしいか。ベクトルからベクトルに影を作ってハッピーと言ってるわけではない。
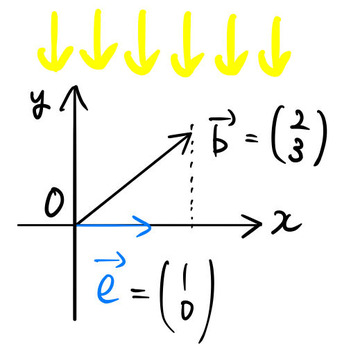
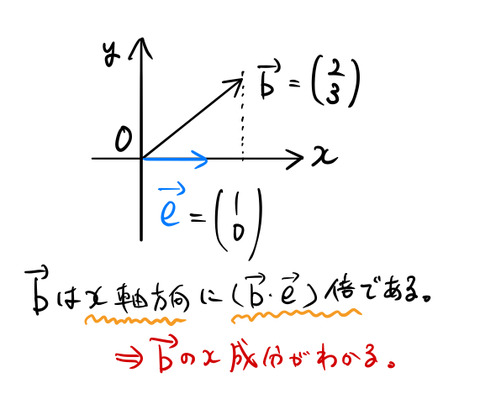
例えば、![]() が
が ![]() 軸方向の単位ベクトル
軸方向の単位ベクトル ![]() である場合を考えよう。ベクトル
である場合を考えよう。ベクトル ![]() を
を![]() として同じように
として同じように ![]() 軸に垂直方向(
軸に垂直方向( ![]() 軸方向)から光を当ててみた図である。
軸方向)から光を当ててみた図である。
いま、影になる部分は青色の単位ベクトルの2倍の長さになっていることを確認して欲しい。そして ![]() であった。2倍という値は、
であった。2倍という値は、![]() の
の ![]() 成分に対応している。つまりは、
成分に対応している。つまりは、![]() に垂直な光を当てて影になる長さは、
に垂直な光を当てて影になる長さは、![]() の
の ![]() 成分と同じになるのである。
成分と同じになるのである。
違う言い方をすれば、今の場合、射影の長さはもともとの ![]() の何倍かを表しているのである。ベクトルは方向もあるので、次のように捉えることができる。
の何倍かを表しているのである。ベクトルは方向もあるので、次のように捉えることができる。
影を作るほうのベクトル(![]() )は、影を作られるほうのベクトル(
)は、影を作られるほうのベクトル(![]() )の方向に射影の長さ倍だけ伸びている。
)の方向に射影の長さ倍だけ伸びている。
これは大きさが1の単位ベクトル ![]() に限らない。
に限らない。![]() に垂直な方向から光を
に垂直な方向から光を ![]() に当てたときにできる射影の長さ
に当てたときにできる射影の長さ ![]() は、
は、![]() が
が ![]() 方向に対して
方向に対して ![]() の大きさの何倍伸びているかを表している。
の大きさの何倍伸びているかを表している。
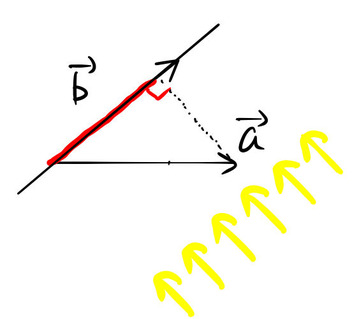
別の光の当て方もある。![]() に垂直な方向から光を当ててみる。
に垂直な方向から光を当ててみる。
この場合も同じく、赤い射影の長さ(この場合は、![]() ) は、
) は、![]() が
が ![]() 方向に
方向に ![]() の射影の長さ倍であるということがわかる。
の射影の長さ倍であるということがわかる。
【補足】
念の為、計算でチェックしておく。ややこしいので飛ばしてもらっても良い。![]() と
と ![]() のなす角を
のなす角を ![]() とする。このとき、
とする。このとき、![]() 方向の大きさ1の単位ベクトルは
方向の大きさ1の単位ベクトルは ![]() である。射影の長さ
である。射影の長さ ![]() が
が ![]() の
の ![]() 倍だとすると以下の式が成り立つ。
倍だとすると以下の式が成り立つ。
![]()
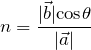
2. ベクトル内積の成分をみる
内積の成分は以下で計算できる。
ベクトル ![]() の成分を
の成分を ![]() 、ベクトルb
、ベクトルb![]() の成分を
の成分を ![]() とすると内積の値は以下のように計算できる。
とすると内積の値は以下のように計算できる。
![]()
2.1 内積のおかげ
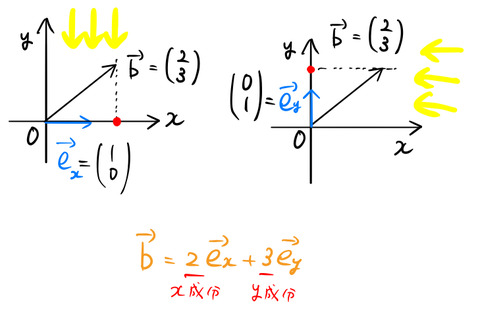
射影の長さの何倍とか何の意味があるの?と思うかもしれない。では、![]() のベクトルに対して、
のベクトルに対して、![]() 軸方向と
軸方向と![]() 軸方向の単位ベクトルとの内積を考えよう。
軸方向の単位ベクトルとの内積を考えよう。
この絵から内積の力がわかるだろうか。
左の図は ![]() 軸方向の単位ベクトルについての内積の絵である。射影の長さが、
軸方向の単位ベクトルについての内積の絵である。射影の長さが、![]() 成分の値に対応するのである。同様に右の図は
成分の値に対応するのである。同様に右の図は ![]() 軸方向の単位ベクトルについての内積の絵である。射影の長さが、
軸方向の単位ベクトルについての内積の絵である。射影の長さが、![]() 成分の値に対応するのである。
成分の値に対応するのである。
単位ベクトルとの内積の値は、内積をとった単位ベクトルの方向の成分である。
単位ベクトル方向の成分の値が分かれば、図のオレンジのようにベクトル ![]() を単位ベクトルで表すことができる。
を単位ベクトルで表すことができる。
2.2 繋げる(線型結合)
![]() の場合でなくても、平面上のすべてのベクトルは、
の場合でなくても、平面上のすべてのベクトルは、![]() 軸方向と
軸方向と![]() 軸方向の単位ベクトルで表すことができる。
軸方向の単位ベクトルで表すことができる。
![]()
![]()
線型結合をつくるための2つのベクトルのことを「基底ベクトル」という。2次元の例で説明したが、3次元の場合は「基底ベクトル」は3つあるし、![]() 次元であれば
次元であれば ![]() 個の独立な「基底ベクトル」が取れる。
個の独立な「基底ベクトル」が取れる。
基底ベクトルは互いに直交している単位ベクトルであると非常に便利である。この基底ベクトルのことを「正規直交基底」という。「正規」は大きさが1になっていることを意味する。この便利さは、高校数学の内容ではなかなか伝わらないと思う。以下の応用になるとわかるのだが…。
2.3 なす角度がわかる
内積の定義式を変形すれば、
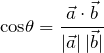
3 ベクトル内積の応用をみる
内積を使って何ができるか、簡単に応用例を説明する。ここからは、高校では学習しない話になる。
3.1 フーリエ級数での例
フーリエ級数はベクトル空間の拡張である、関数空間(矢印を関数に拡張した空間)における話になる。また、関数空間においては内積の定義が異なる。
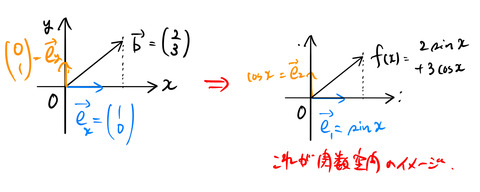
関数空間の基底は関数である。内積は関数同士をかけて積分するように決められることが多い。例として2次元の関数空間における2個の基底 ![]() を考える。この基底の線型結合で作られる関数なんて限られているだろう。
を考える。この基底の線型結合で作られる関数なんて限られているだろう。
![]()
この ![]() において、基底
において、基底 ![]() の成分は3である。この3は 基底
の成分は3である。この3は 基底 ![]() の「大きさ」の3倍であることを意味するのであった(1.3で述べた射影の長さの意味に対応)。ベクトルの「大きさ」はイメージできるが、「関数の大きさ」とは。それには内積の定義が必要である。
の「大きさ」の3倍であることを意味するのであった(1.3で述べた射影の長さの意味に対応)。ベクトルの「大きさ」はイメージできるが、「関数の大きさ」とは。それには内積の定義が必要である。
ここでの内積を定義しておこう。![]() と
と![]() の内積を、
の内積を、
![]()
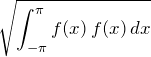
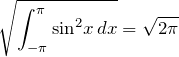
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{-\pi}^{\pi} {\rm sin}x \,{\rm cos}x \, dx&=&\frac{1}{2}\int_{-\pi}^{\pi} {\rm sin}2x \, dx\\&=& \frac{1}{2} \left[ -\frac{1}{2}{\rm cos}2x \right]_{-\pi}^{\pi}\\&=& 0\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0f70b3708eb0c440a8f570ab2fa61b28_l3.png)
![]()
正規直交基底が分かれば、![]() と
と ![]() の内積が、
の内積が、![]() の
の ![]() における成分
における成分 ![]() であることがわかるだろう。つまり、
であることがわかるだろう。つまり、
![Rendered by QuickLaTeX.com \begin{eqnarray*}a_1 &\equiv & \int_{-\pi}^{\pi} f(x)\;\frac{1}{\sqrt{2\pi}}{\rm sin}x \,dx \\&=& \int_{-\pi}^{\pi} \left[ 2{\rm sin}x + 2{\rm cos}x \right] \;\frac{1}{\sqrt{2\pi}}{\rm sin}x&=& 2\sqrt{2\pi}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9f607ea09bc5e30f304029382dfdce46_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}b_1 &\equiv & \int_{-\pi}^{\pi} f(x)\;\frac{1}{\sqrt{2\pi}}{\rm cos}x \,dx \\&=& \int_{-\pi}^{\pi} \left[ 2{\rm sin}x + 2{\rm cos}x \right] \;\frac{1}{\sqrt{2\pi}}{\rm cos}x&=& 3\sqrt{2\pi}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-da272937b4949fb240e299230d1d06fe_l3.png)
![]()
無限次元に拡張すれば、おなじみのフーリエ級数の式を得るだろう。ここで、![]() ,
, ![]() などをフーリエ係数という。ベクトル空間でのベクトルの成分とおなじイメージである。フーリエ係数を求めることは、ざっくりいえば、
などをフーリエ係数という。ベクトル空間でのベクトルの成分とおなじイメージである。フーリエ係数を求めることは、ざっくりいえば、![]() がどのような波の重ね合わせで作られているか調べるのと同じである。
がどのような波の重ね合わせで作られているか調べるのと同じである。
cosとsinの直交性があるから、内積をとることでcosとsinの積は消えて、フーリエ係数が簡単に求められる。これ以上はここでは述べない。
3.2 状態が似ているか?(量子力学の例)
量子力学では状態をベクトルにしてしまう(状態ベクトル)。関数空間より抽象的な概念であり、新たに内積の定義などを行う必要があるので詳細は立ち入らない。以下では状態ベクトルの直交性について簡単に説明しておく。
平面ベクトルが直交しているとは、ベクトル同士が90°異なる方向を向いていることである。状態ベクトルのイメージも同じである。大きさが1の2つの状態ベクトルを考えよう。状態ベクトルが直交しているとは、2つの状態が全く違う状態を表しているということである。
ベクトル同士が同じ方向を向いていたら、そのベクトルはよく似ているといえるだろう。2つの状態ベクトルが似ている状態ならば、当然状態ベクトルの内積も大きくなる。
抽象的な話になるのでここまでで留めておきたい。
3.3 文章が似ているか?(cos類似度の例)
量子力学の例で述べたように、ベクトルが似ているとはベクトル同士が同じ方向を向いていることだと考えられる。2つのベクトルの方向を調べるためには、なす角 ![]() を調べればよかった。ベクトルの大きさが1(正規化したベクトル)の場合は、
を調べればよかった。ベクトルの大きさが1(正規化したベクトル)の場合は、
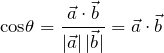
文章をベクトル化したときの、なす角度 ![]() を「コサイン類似度」とよぶ。コサイン類似度が大きければ文章は似ている(近い方向を向いている)し、コサイン類似度が小さければ文章は似ていない(違う方向を向いている)。
を「コサイン類似度」とよぶ。コサイン類似度が大きければ文章は似ている(近い方向を向いている)し、コサイン類似度が小さければ文章は似ていない(違う方向を向いている)。
ディストピア小説であるジョージ・オーウェルの『1984』とファニーなセルバンテスの『ドン・キホーテ』はコサイン類似度は小さいと言えそうである。一方で『1984』とレイ・ブラッドベリの『華氏451度』は同じディストピア小説としてコサイン類似度は高そうである。(『華氏451度』を読んでいないので推測である。)
私は人間なのでだいたいのコサイン類似度しかわからない。しかし、文章をベクトル化して機械による判別を行えば、いろいろな文章が似てるか似ていないか見分けることができるだろう。文章を分類する上で、ベクトルの内積の重要性がわかったと思う。
4. まとめ
ポップな絵を使ったベクトル内積の説明とうってかわって、後半の応用はやや複雑である。ともかく、内積がいろいろなところで使われていてめっちゃ便利だということを知ってもらえれば嬉しい。
お読みいただきありがとうございました。