【テイラー展開】coth(x)の展開

ランジュバン関数などに現れる coth( $x$ )= $\frac{1}{{\rm tanh}(x)}$ の x=0近傍におけるテイラー展開についてまとめておく。指数関数の展開を用いた方法は、様々な関数について有効であるので覚えておいてほしい。

参考：ランジュバン関数・ブリルアン関数の展開

参考：双曲線関数tanh(x)のテイラー展開（x~0）

知っておくべき前提事項は以下の３点である。

1. 予備知識
2. cothの展開
- 2.1 分母の展開
- 2.2 分子の展開

1. 予備知識

1.1 双曲関数（ハイパボリック〇〇）

$\begin{eqnarray*}{\rm sinh}(x)&=&\frac{e^x-e^{-x}}{2}\\{\rm cosh}(x)&=&\frac{e^x+e^{-x}}{2}\\{\rm tanh}(x)&=&\frac{{\rm sinh}(x)}{{\rm cosh}(x)}=\frac{e^x+e^{-x}}{e^x-e^{-x}}\end{eqnarray*}$

は前提として覚えておく。

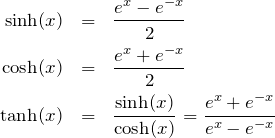
1.2 指数関数の展開

$\begin{eqnarray*}e^{x} =1+x+\frac{1}{2!}x^2 + \frac{1}{3!}x^3+\cdots\\e^{-x}=1-x+\frac{1}{2!}x^2 - \frac{1}{3!}x^3+\cdots\end{eqnarray*}$

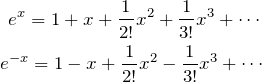
のように展開できる。

1.3 1/(1+x)の展開

$\begin{eqnarray*} \frac{1}{1-x}=1+x+x^2+x^3+\cdots \end{eqnarray*}$

これは $\sum_{k=1}^{\infty} x^{k-1}=\frac{1}{1-x}$ のように無限等比級数の和の関係式を表す。ここでは、

$\begin{eqnarray*}\frac{1}{1+ax^2}=1-ax^2+a^2x^4-a^3x^6\cdots\end{eqnarray*}$

の形を用いる。(上の式で $x\rightarrow -ax^2$ と置き換える。)

2. cothの展開

$\begin{eqnarray*}{\rm coth}(x)=\frac{1}{{\rm tanh}(x)}=\frac{{\rm cosh}(x)}{{\rm sinh}(x)}=\frac{e^{x}+e^{-x}}{e^x-e^{-x}}\end{eqnarray*}$

を展開する

方針：分母、分子をそれぞれ級数展開する。

2.1 分母の展開

$\begin{eqnarray*}e^{x}-e^{-x} &=& (1+x+\frac{1}{2}x^2+\frac{1}{3!}x^3+\cdots)\\&-&(1-x+\frac{1}{2}x^2-\frac{1}{3!}x^3+\cdots)\\&=&2(x+\frac{1}{3!}+\cdots)\end{eqnarray*}$

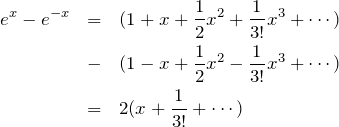
と展開できるので、この逆数をさらに展開する。

$\begin{eqnarray*}\frac{1}{2\Bigl(x+\frac{1}{3!}+\cdots\Bigr)} &=& \frac{1}{2x} \Bigl(\frac{1}{1+\frac{1}{6}x^2+\cdots}\Bigr)\\&=&\frac{1}{2x} \Bigl[ 1-\frac{1}{6}x^2+O(x^4) \Bigr]\end{eqnarray*}$

最後の行では、 $\frac{1}{1-ax^2}$ の展開式を括弧内に用いた。（ $x^4$ 次以上の高次の項については $O(x^4)$ とした。）

2.2 分子の展開

$\begin{eqnarray*}e^{x}+e^{-x} &=& (1+x+\frac{1}{2}x^2+\frac{1}{3!}x^3+\cdots)\\&+&(1-x+\frac{1}{2}x^2-\frac{1}{3!}x^3+\cdots)\\&=&2(1+\frac{1}{2}x^2 + O(x^4))\end{eqnarray*}$

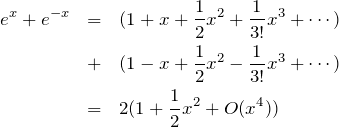
と展開できる。したがって、

$\begin{eqnarray*}\frac{e^{x}+e^{-x}}{e^{x}-e^{-x}} &=& 2\Bigl[ 1 + \frac{1}{2}x^2+O(x^4)\Bigr]\Bigl[ \frac{1}{2x} \bigl(1-\frac{1}{6}x^2+O(x^4)\bigr)\Bigr]\\&=& \frac{1}{x}\Bigl[ \bigl( 1+\frac{1}{2}x^2 \bigr) \bigl( 1-\frac{1}{6}x^2 \bigr) + O(x^4)\Bigr]\\&=& \frac{1}{x}\bigl[ 1+\frac{1}{3}x^2 + O(x^4) \bigr]\\&=&\frac{1}{x} + \frac{x}{3} + O(x^3)\end{eqnarray*}$

となる。

結果をまとめておく。

coth(x)の展開（x~0)

$\begin{eqnarray*}{\rm coth}(x)= \frac{1}{x} + \frac{x}{3} + O(x^3)\end{eqnarray*}$