全記事一覧 > 物理 > X線回折

X線回折の解析・計算の基礎（ディフラクトメーター）

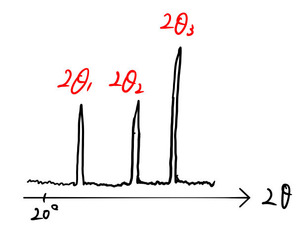
　X線回折は固体物理で重要な役割を果たす。ここでは、ディフラクトメータによるX線回折の解析の基礎を説明する。ディフラクトメータでは 2\theta でスキャンしていき、Braggの回折条件を満たす角度のときに回折によるピークが確認できる（下図）。

IMG_A013C9C221D4-1

　このピークから何が得られるかを解説していく。面心立方格子(FCC)や体心立方格子(BCC)などの立方晶系の面間隔の式は簡単であるので、立方晶系を例にとって解説する。

1. X線回折

　X線は波である。したがって、２つの波があれば強め合ったり弱めあったりするように、X線も強め合うことがある。どのような条件で結晶に入射したX線が強め合うかを調べるために、Braggの式が必要である。

1.1 Braggの式

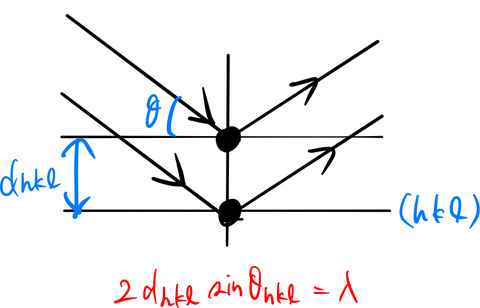
　X線が結晶で回折する条件はBraggの式で与えられる。

Braggの式

 

    \begin{eqnarray*}2d_{hkl}{\rm sin}\theta_{hkl} = \lambda \quad \cdots (1)\end{eqnarray*}

　
　d_{hkl}：(h,k,l) 面の面間隔
　　\theta_{hkl}：(h,k,l) 面におけるBragg角（図を参照）
　　\lambda：入射するX線の波長（定数、既知）

　ディフラクトメータでは 2\theta を小さい値から大きい値まで変えていく。Braggの式を満たすある (h,k,l) 面のときにX線が回折する。

IMG_AFBE4FD7290F-1

　入射するX線の波長 \lambda は、例えば、特性X線のCu K_{\alpha} を使うときは、1.5418 Åである。当たり前だが、実験では何のX線を使っているか知っておく必要がある。

1.2 立方晶系の面間隔の式

　立方晶系は対称性が良いので、面間隔の式は簡単な形になる。

立方晶系の面間隔の式

 

    \begin{eqnarray*}d_{hkl}=\frac{a}{\sqrt{h^2 + k^2 + l^2}}\quad \cdots (2) \end{eqnarray*}

　　a：格子定数（求めたい値、未知）

参考：ミラー指数と逆格子ベクトル、面間隔、幾何学的関係

　今回、解析で使う関係式は以下の２つの式である。
　　(1) Braggの式
　　(2) 面間隔の式

2. 解析してみる

IMG_A013C9C221D4-1

を解析してみよう。式(1)(2)を使う上で、まず既知の値と未知の値をはっきりさせておく。

　　　既知：入射X線の波長 \lambda
　　　既知：各ピークの \theta の値
　　　未知：それぞれのピークの面指数 (h,k,l)
　　　未知：格子定数 a

2.1 Braggの式を変形する

　求めたい面間隔に注目してBraggの式(1)を変形する。

    \begin{eqnarray*}d_{hkl}=\frac{\lambda}{2{\rm sin}\theta_{hkl}}\end{eqnarray*}

　ディフラクトメータでは \theta をだんだん大きくしていく。X線の波長の場合はだいたい \theta が20°から80°くらいまでの時に回折がおこることに注意する。

　簡単のため0\; {\rm [rad]} から角度を大きくしていく場合を考える。\theta が大きくなると、左辺の面間隔はだんだん小さくなっていく。これから重要な帰結を得る。

X線回折に関する重要なこと１

 

0 [rad]から角度を大きくしていくとき、面間隔の最も大きい面が最初に回折する。

　そしてここで、面間隔の式(2)を見て欲しい。a は格子定数で変わらない値なので、「面間隔の最も大きい面」は \sqrt{h^2+k^2+l^2} が最も小さい面である。

消滅則がないBCCの場合は、(h\; k\;l)=\{1\;0\;0\} 面である。消滅則のあるFCCの場合は　(h\; k\;l)=\{1\;1\;1\} である。

X線回折に関する重要なこと２

 

0 [rad]から角度を大きくしていくとき、\sqrt{h^2+k^2+l^2}が最小になる (h\;k\;l) 面が最初に回折する。

2.2 面指数を求めてみる

　上記の事項から、単純立法格子の場合を考えてみる。単純立法格子では消滅則はないので、とりうる面指数 (h\; k\;l) に制約はない。\theta_1, \theta_2, \theta_3の面指数を決定する。それぞれの記号については、以下の通り設定する。

　 (h_1\; k_1\;l_1)：\theta_1 のBragg角で回折がおこる面の面指数
　 (h_2\; k_2\;l_2)：\theta_2 のBragg角で回折がおこる面の面指数
　 (h_3\; k_3\;l_3)：\theta_3 のBragg角で回折がおこる面の面指数
　 d_{h_1 k_1 l_1}：面指数 (h_1\; k_1\;l_1) の面における面間隔
　 d_{h_2 k_2 l_2}：面指数 (h_2\; k_2\;l_2) の面における面間隔
　 d_{h_3 k_3 l_3}：面指数 (h_3\; k_3\;l_3) の面における面間隔

IMG_A013C9C221D4-1

　単純立法格子（消滅則のない）のとき\sqrt{h^2+k^2+l^2} を小さい順に10個書くと。

　　h^2+k^2+l^2 = 1 \rightarrow (100)=(h_1\; k_1\;l_1) に対応
　　h^2+k^2+l^2 = 2 \rightarrow (110)=(h_2\; k_2\;l_2) に対応
　　h^2+k^2+l^2 = 3 \rightarrow (111)=(h_3\; k_3\;l_3) に対応
　　h^2+k^2+l^2 = 4 \rightarrow (200) に対応
　　h^2+k^2+l^2 = 5 \rightarrow (210) に対応
　　h^2+k^2+l^2 = 6 \rightarrow (211) に対応
　　h^2+k^2+l^2 = 8 \rightarrow (220) に対応
　　h^2+k^2+l^2 = 9 \rightarrow (300),(221) に対応
　　h^2+k^2+l^2 = 10 \rightarrow (310) に対応
　　h^2+k^2+l^2 = 11 \rightarrow (311) に対応

(1)Braggの式と(2)面間隔の式から d_{hkl} を消去して、

    \begin{eqnarray*}\frac{\lambda}{2 {\rm sin}\theta_{hkl} }=\frac{a}{\sqrt{h^2+k^2+l^2} } \\ \\\therefore a=\frac{\lambda \sqrt{h^2+k^2+l^2}}{2{\rm sin}\theta_{hkl}}\end{eqnarray*}

になる。各々のピークより格子定数 a の値が計算できる。このとき、計算される格子定数をそれぞれ、a_1,a_2,a_3 などととすれば、

    \begin{eqnarray*}a_1 \approx a_2 \approx a_3\end{eqnarray*}

である。なぜなら、格子定数は定数であるためもちろん一定になる。

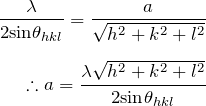
2.3 格子定数を計算する

Braggの式から、　

    \begin{eqnarray*}　d_{100}=\frac{\lambda}{2{\rm sin}\theta_1}\\　d_{110}=\frac{\lambda}{2{\rm sin}\theta_2}\\　d_{111}=\frac{\lambda}{2{\rm sin}\theta_3}\\　\end{eqnarray*}

を求めた後に、面間隔の式から、　

    \begin{eqnarray*}　a_1&=&d_{100}\sqrt{1^2+0^2+0^2}=d_{100}\\　a_2&=&d_{110}\sqrt{1^2+1^2+0^2}=\sqrt{2}d_{110}\\　a_3&=&d_{111}\sqrt{1^2+1^2+0^2}=\sqrt{3}d_{111}　\end{eqnarray*}

で格子定数を求める。

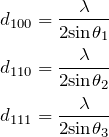
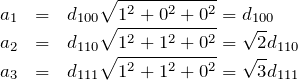
3. まとめ

　ピークから面指数を求めて、格子定数を求めた。X線回折の基本的な計算なので習得しておくべきである。


2件のコメント

  1. 森野翔太

    （222）はh^2+k^2+l^2=8にはならないのでは？

    返信
    • batapara

      すみません、(220)の間違いです。どうもありがとうございます。

      返信

コメントを残す

メールアドレスが公開されることはありません。