ミラー指数![]() の面と逆格子ベクトル
の面と逆格子ベクトル![]() などの幾何学。
これはほとんどベクトルの問題であるため、説明するための図が多くなっている。
などの幾何学。
これはほとんどベクトルの問題であるため、説明するための図が多くなっている。
前提知識
ミラー指数
以下の3点を通る平面を ![]() とする。
とする。
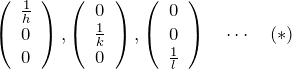
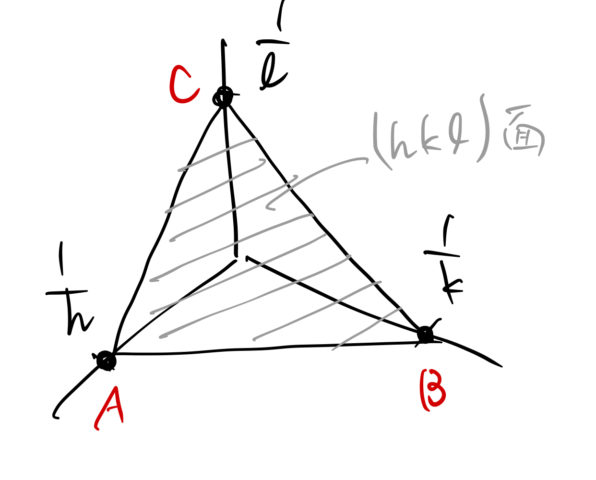
三次元空間の3点を決めれば平面はただ一つに決まるため、この ![]() で面を表す。 このように決められた面指数をミラー指数とよぶ。
で面を表す。 このように決められた面指数をミラー指数とよぶ。
3点をA,B,Cとすると図のような平面になる。
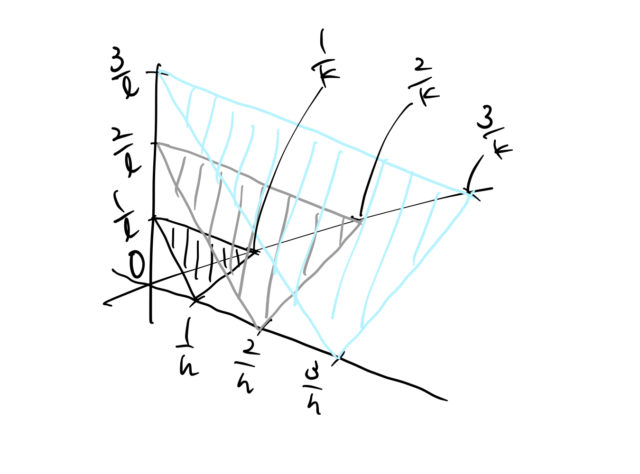
また、ミラー指数 ![]() は平面群 をあらわす。 そのため、図のように平面は無数にある。各平面は以下の3点によって決定する。
は平面群 をあらわす。 そのため、図のように平面は無数にある。各平面は以下の3点によって決定する。
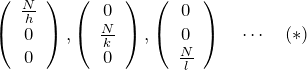
ここで、![]() は整数である。
は整数である。
ベクトルの外積
ここでは正規直交基底を考える。
3点A,B,Cで決まる平面と垂直なベクトルは、図のように平面内の2つの独立なベクトルの外積で求めることができる。
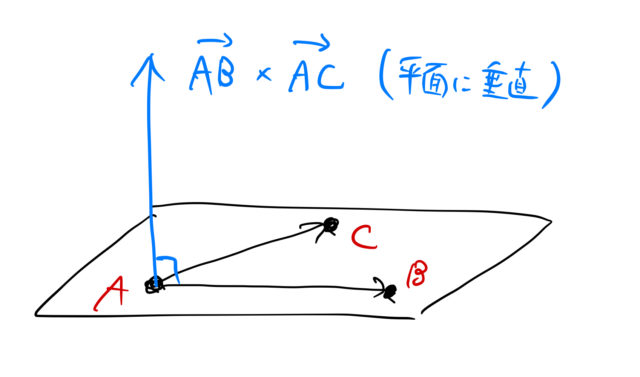
式(*)の3点をA,B,Cの空間座標とすると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{AB}\times \vec{AC}&=& \left[ \begin{array}{c} -\frac{1}{h}\\ \\ \frac{1}{k}\\\\0 \end{array}\right] \times \left[ \begin{array}{c} -\frac{1}{h}\\\\0\\\\\frac{1}{l} \end{array}\right] \\ &=& \left[ \begin{array}{c} \frac{1}{kl}\\\\\frac{1}{hl}\\\\\frac{1}{hk} \end{array}\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4aea5df7a2ae8defbafd98d2dc90b849_l3.png)
このベクトルを ![]() 倍(定数倍)して、
倍(定数倍)して、
![]()
を得る。定数倍しただけなので、もとのベクトル ![]() と平行である。 このベクトルが2つのベクトル
と平行である。 このベクトルが2つのベクトル ![]() と垂直であることは、内積が0になることからわかる。
と垂直であることは、内積が0になることからわかる。
ミラー指数 ![]() で表される面に垂直なベクトルが
で表される面に垂直なベクトルが ![]() で表されることは重要である。
で表されることは重要である。
ミラー指数と逆格子ベクトルの幾何学的関係
(hkl)面上の点(x,y,z)が満たす式
ここでは正規直交基底によってベクトルの成分が定められているとする。
まず、![]() で張られた(
で張られた(![]() )面上にある点
)面上にある点 ![]() が満たす式を求める。 すなわち、
が満たす式を求める。 すなわち、![]() 面の平面の方程式を求める。
面の平面の方程式を求める。
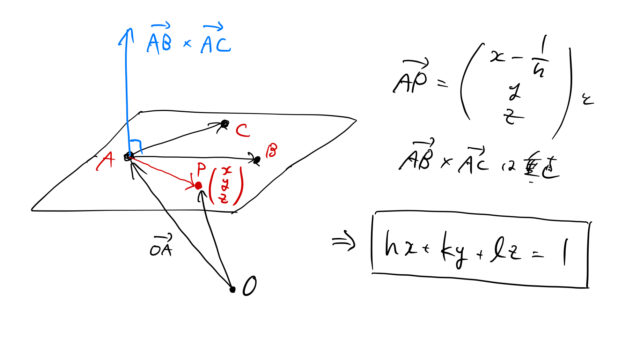
原点を ![]() にとると図より
にとると図より
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{OA}= \left[ \begin{array}{c} \frac{1}{h}\\0\\0 \end{array}\right],\quad \vec{AP}=\left[ \begin{array}{c} x-\frac{1}{h}\\y\\z \end{array}\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b646a6da6ec56f7f0de3c4149d3ab29a_l3.png)
となる。![]() は(
は(![]() )面上のベクトルであるため、
)面上のベクトルであるため、![]() 面に垂直なベクトル
面に垂直なベクトル
![]()
と垂直になる。
したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} && \left[ \begin{array}{c} h\\k\\l \end{array}\right] \cdot \vec{AP}=0\\ \Leftrightarrow \quad && hx+ky+lz=1\quad\cdots\quad(1) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-25c98cf34d5b3f17213831190f1a11b1_l3.png)
の関係式を得る。
先に説明したようにミラー指数 ![]() は平面群をなす。 これより下の重要な式を得る。
は平面群をなす。 これより下の重要な式を得る。
ミラー指数 ![]() 面にある点
面にある点![]() の条件は以下のようになる。
の条件は以下のようになる。
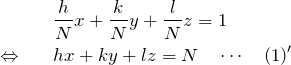
(hkl)面と逆格子ベクトル
(![]() )面上の点
)面上の点 ![]() について、この座標
について、この座標 ![]() は基底ベクトル
は基底ベクトル ![]() に対する座標である。 回りくどいようだが、
に対する座標である。 回りくどいようだが、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{l}\equiv\vec{OP}=x\vec{a}_1 + y\vec{a}_2 +z\vec{a}_3\equiv \left[\begin{array}{c} x\\ y\\ z \end{array}\right]_a \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8c86e31076438fad08aa698e65edbb48_l3.png)
の意味である。![]() は互いに直交してなくても良い(正規直交基底でなくても良い)。
は互いに直交してなくても良い(正規直交基底でなくても良い)。 ![]() はそのベクトル成分が
はそのベクトル成分が ![]() の成分であることを意味する。
の成分であることを意味する。
ここで、逆格子ベクトル ![]()
![]() を用いて下のベクトルを定義する。
を用いて下のベクトルを定義する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{g}=2\pi(h\vec{b}_1+k\vec{b}_1+l\vec{b}_3) \equiv 2\pi \left[\begin{array}{c} h\\ k\\ l \end{array}\right]_b \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-c7f55937f6093bf64291dcd4178eb802_l3.png)
![]() はそのベクトル成分が
はそのベクトル成分が ![]() の成分であることを意味する。 (一般には
の成分であることを意味する。 (一般には ![]() であることに注意する。)
であることに注意する。)
![]() の関係から、
の関係から、![]() は
は ![]() と垂直である。 実際、ていねいに計算を書くと、
と垂直である。 実際、ていねいに計算を書くと、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{g}\cdot\vec{AB} &=& \left[\begin{array}{c} h\\ k\\ l \end{array}\right]_b \cdot \left[\begin{array}{c} -\frac{1}{h}\\\frac{1}{k}\\0 \end{array}\right]_a\\ &=& (h\vec{b}_1+k\vec{b}_2+l\vec{b}_3)\cdot\left(-\frac{1}{h}\vec{a}_1+\frac{1}{k}\vec{a}_2+0\,\vec{a}_3\right)\\ &=& h\vec{b}_1\cdot\left(-\frac{1}{h}\vec{a}_1+\frac{1}{k}\vec{a}_2+0\,\vec{a}_3\right)\\ &+&k\vec{b}_2\cdot\left(-\frac{1}{h}\vec{a}_1+\frac{1}{k}\vec{a}_2+0\,\vec{a}_3\right)\\ &+&l\vec{b}_3\cdot\left(-\frac{1}{h}\vec{a}_1+\frac{1}{k}\vec{a}_2+0\,\vec{a}_3\right)\\ &=&0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-044682ea5044bd1af8da33b20b6a3047_l3.png)
となる。![]() も同様に示すことができる。 この結果は、
も同様に示すことができる。 この結果は、 ![]() がミラー指数
がミラー指数 ![]() の平面群に垂直なベクトルであること を意味する。
の平面群に垂直なベクトルであること を意味する。
![]() は
は ![]() で表されているため逆格子空間内の点 (
で表されているため逆格子空間内の点 (![]() ) を指すベクトルである。
) を指すベクトルである。
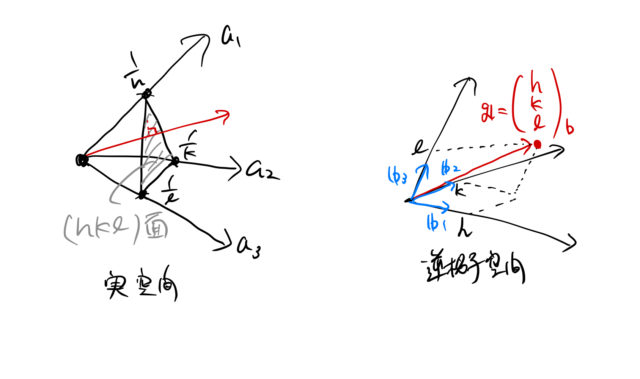
このことは実空間で表された ![]() 面が逆空間では点で表されていることを意味する。 ある平面を実空間で考えるかわりに、その平面に垂直なベクトルを逆空間で考えるのである。
面が逆空間では点で表されていることを意味する。 ある平面を実空間で考えるかわりに、その平面に垂直なベクトルを逆空間で考えるのである。
[*] 逆格子ベクトルの定義: この実空間の基底ベクトル ![]() に対して、逆空間で定義された逆格子ベクトル
に対して、逆空間で定義された逆格子ベクトル ![]() は
は
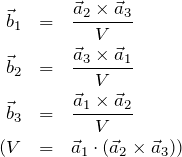
で定義される。![]() は
は ![]() で作られる平行六面体の体積である(
で作られる平行六面体の体積である(![]() が互いに直交しているならば直方体、また、大きさが同じで直交しているならば立方体になる)。
が互いに直交しているならば直方体、また、大きさが同じで直交しているならば立方体になる)。
また、その定義より
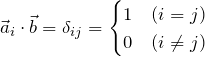
の関係を満たす。![]() はクロネッカーのデルタである(ここでは
はクロネッカーのデルタである(ここでは ![]() の形になるように逆格子ベクトルを定義していないことに注意する)。
の形になるように逆格子ベクトルを定義していないことに注意する)。
(hkl)面の面間隔
(![]() )で表された平面群の面間隔を求める。
)で表された平面群の面間隔を求める。
まず、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{l}= \left[\begin{array}{c} x\\ y\\ z \end{array}\right]_a \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8226641e9b5098ec7a6b6cfea947a2d2_l3.png)
に戻って、![]() と
と![]() の内積をとると、
の内積をとると、
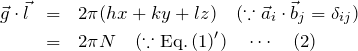
となる。
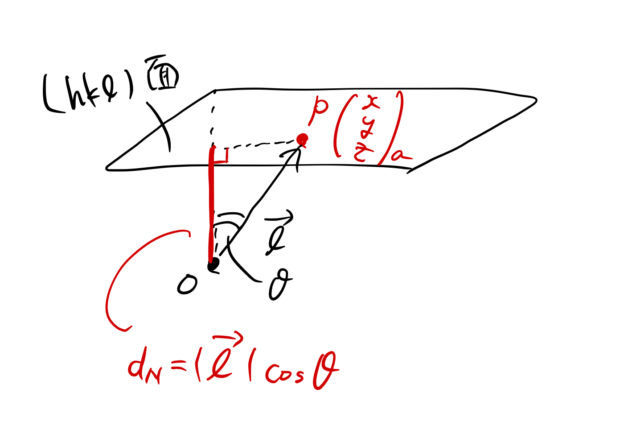
図より、原点から(![]() )面のうち1つの面までの距離
)面のうち1つの面までの距離 ![]() は
は
![]()
となる。![]() は
は ![]() と面(
と面(![]() )に垂直なベクトルとのなす角である。 面(
)に垂直なベクトルとのなす角である。 面(![]() )に垂直なベクトルは
)に垂直なベクトルは ![]() であったから、式(2)の結果を用いて、
であったから、式(2)の結果を用いて、
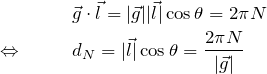
となる。
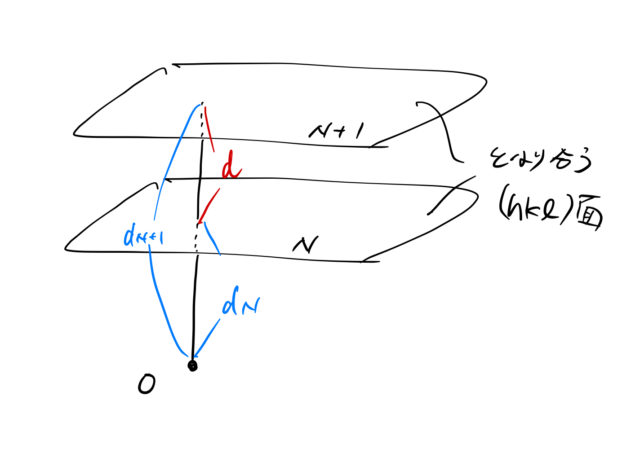
したがって面間隔 ![]() は、図より
は、図より
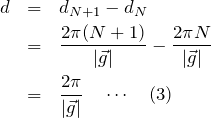
となる。
(![]() )面の面間隔
)面の面間隔 ![]() は
は ![]() で表すことができる。
で表すことができる。
![]()
立方晶系の面間隔
![]() を求める。 とくに立方晶系の場合は格子定数を
を求める。 とくに立方晶系の場合は格子定数を ![]() として、
として、
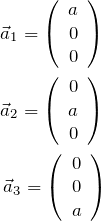
より、逆格子ベクトルは
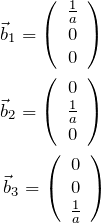
となる。![]() が互いに直交するため、逆格子ベクトルも互いに直交する。 また、
が互いに直交するため、逆格子ベクトルも互いに直交する。 また、
![]()
となる。
したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} |\vec{g}|^2&=& \left|2\pi\left[\begin{array}{c} h\\k\\l \end{array}\right]_b\right|^2 \\\\ &=&(2\pi)^2(h^2\vec{b}_1^2 + k\vec{b}_2^2 + l\vec{b}_3^2) \\ &=& \frac{(2\pi)^2(h^2+k^2+l^2)}{a^2}\\ \therefore \quad |\vec{g}|&=&\frac{2\pi\sqrt{h^2+k^2+l^2}}{a}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1bc41319d26c29ac7a4b931b4eac83f1_l3.png)
これより立方晶系の面間隔が求められた。
格子定数 ![]() の立方晶系における
の立方晶系における ![]() 面の面間隔
面の面間隔 ![]() は以下の通りである。
は以下の通りである。
![]()