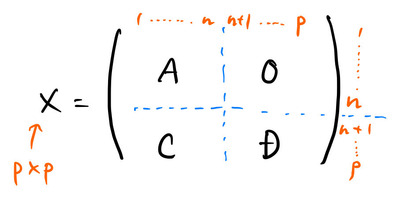
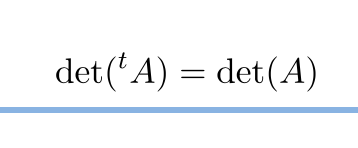![]() が
が ![]() 次正方行列、
次正方行列、![]() が
が ![]() 次正方行列のとき、
次正方行列のとき、
零行列  があるときの行列式
があるときの行列式
![]()
が成立することの証明です。
1. n次正方行列の行列式
各種記号については、参考:置換σを用いた行列式の定義を参照されたし。
定義:![]() 次正方行列
次正方行列 ![]() の行列式 det(
の行列式 det(![]() ) は、
) は、
![]()
2. det(A B O D)=det(A)det(D)
置換の扱いに慣れていないと難しいかもしれない。
2.1 証明
【証明】 ![]() が
が ![]() 次正方行列、
次正方行列、![]() が
が ![]() 次正方行列であるため、
次正方行列であるため、![]() 次正方行列を
次正方行列を ![]() とする。
とする。
![]()
![]()
![]()
行列式の定義式(*)の![]() の、条件(1)を満たす項に注目する。
の、条件(1)を満たす項に注目する。
ここで、赤色の項について、![]() が条件(2)を満たす場合を考える。つまり、
が条件(2)を満たす場合を考える。つまり、![]() の中に1つでも
の中に1つでも ![]() より大きい数字がある場合は、条件(2)より
より大きい数字がある場合は、条件(2)より
![]()
![]()
![]()
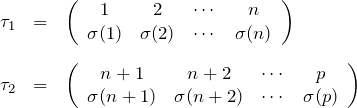
![]()
したがって![]() の行列式(*)は、
の行列式(*)は、
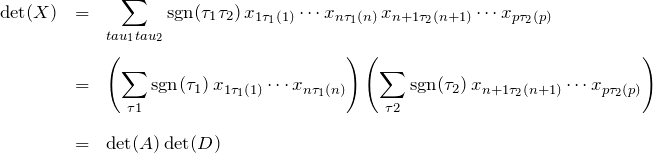
もう1つの関係式
![]()
転置行列の行列式
![]()
を用いればよい。
2.2 例題
例題
次の行列式を計算せよ。
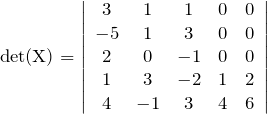
【解答】行列 ![]() を以下のように置く。
を以下のように置く。
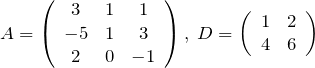
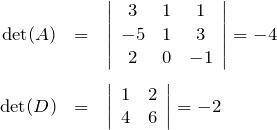
![]()
3. まとめ
この行列式の関係は非常にわかりやすい式であるが、証明は見かけ以上に難しく複雑である。例題を見ればわかるように、零行列 ![]() があるときに非常に強力な武器になるので覚えておいてほしい。
があるときに非常に強力な武器になるので覚えておいてほしい。