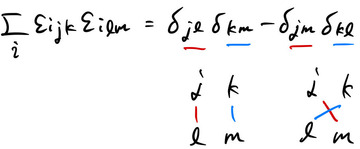電磁気学では外積計算が多い。さらにベクトル解析では学ぶ様々な公式は覚えにくい。しかし、レヴィ=チヴィタの記号![]() を習得すればベクトル解析で学ぶような
を習得すればベクトル解析で学ぶような ![]() などの公式は即座に導ける。この証明は記事の最後で扱った。
などの公式は即座に導ける。この証明は記事の最後で扱った。
1. レヴィチ=ヴィタを定義する
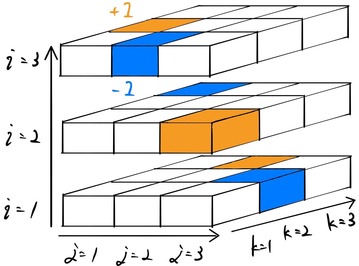
![]() は3階の反対称テンソルである。反対称とは添字の入れ替えに対して符号が変わる、すなわち、
は3階の反対称テンソルである。反対称とは添字の入れ替えに対して符号が変わる、すなわち、 ![]() と
と![]() の入れ替えに対して、
の入れ替えに対して、
![]()
が成り立つ。
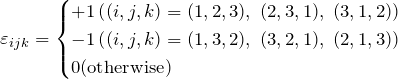
”otherwise”の例として、
ベクトル外積を計算する上で重要な公式:
![]()
がある。
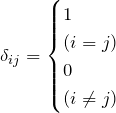
で表される。覚え方は共通の指数
図的に表すと左辺は、
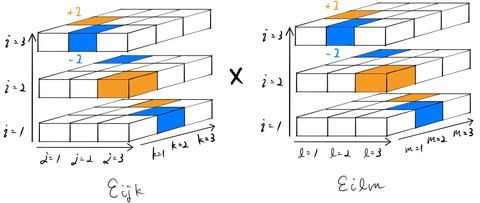
となり、2つのレヴィ=チヴィタ記号の積を与える(![]() で和をとる)。
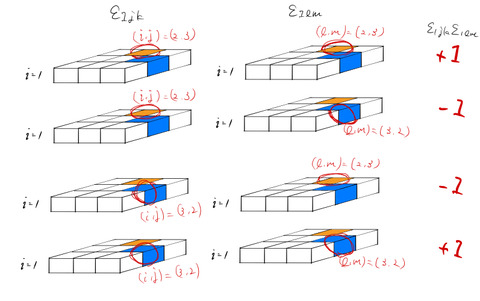
で和をとる)。![]() のとき、具体的に一番下の段だけ取り出して考えると、
のとき、具体的に一番下の段だけ取り出して考えると、
のようになる。ここでは、要素が0になる![]() のすべてが
のすべてが![]() でない4通りを考えた。得られる値は明らかに
でない4通りを考えた。得られる値は明らかに![]() か
か![]() のみであり、
のみであり、![]() と表すことができる。
と表すことができる。
2. ベクトル外積の表現
ベクトル![]() のベクトル積(外積)の
のベクトル積(外積)の![]() 成分は、
成分は、
![Rendered by QuickLaTeX.com \begin{eqnarray*}[{\bf A}\times{\bf B}]_i &=& A_j B_k -A_k B_j\\&=&\sum_{j,k} \varepsilon_{ijk}A_j B_k\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-85e28fb0546a1c1ee0b33f16fa2c9124_l3.png)
で表すことができる。
![]()
のような
3. ベクトル三重積の計算
以下の計算に現れる はダミーの添え字ですべての和をとることを意味する。例えば、
はダミーの添え字ですべての和をとることを意味する。例えば、 については
については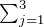 をとる。
をとる。
最後の行で、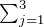 を実行して成分ごとの積の和(ベクトルの内積)をとった。この結果から、ベクトル三重積の公式、
を実行して成分ごとの積の和(ベクトルの内積)をとった。この結果から、ベクトル三重積の公式、
を得る。 これは「BAC-CAB則」として知られている。「バックキャブ」とでも唱えて覚える。
ここで、ラプラス演算子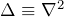 とした。
とした。
![Rendered by QuickLaTeX.com \begin{eqnarray*}\Bigl[ {\bf A}\times ({\bf B}\times{\bf C}) \Bigr]_i&=&\varepsilon_{ijk} A_j \bigl({\bf B}\times {\bf C}\bigr)_k\\&=&\varepsilon_{ijk} A_j \varepsilon_{klm} B_l C_m\\&=&\varepsilon_{ijk}\varepsilon_{klm} A_j B_l C_m\\&=&\varepsilon_{kij}\varepsilon_{klm} A_j B_l C_m \quad(\because \varepsilon_{ijk}=-\varepsilon_{ikj}=\varepsilon_{kij})\\&=& (\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl})A_j B_l C_m\\&=& A_j B_i C_j - A_j B_j C_i\\&=& B_i (A_j C_j) - C_i (A_j B_j)\\&=& B_i ({\bf A}\cdot {\bf C}) - C_i ({\bf A}\cdot {\bf B})\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-486cfc0b37b246d607ba10511a69cfba_l3.png)
最後の行で、
![]()
を得る。 これは「BAC-CAB則」として知られている。「バックキャブ」とでも唱えて覚える。
3.1 例:rot(rot(A))
![]() はマクスウェル方程式から波動方程式を導く過程などでよく現れる式であるが、上記の「BAC-CAB則」を用いると容易に計算できる。
はマクスウェル方程式から波動方程式を導く過程などでよく現れる式であるが、上記の「BAC-CAB則」を用いると容易に計算できる。
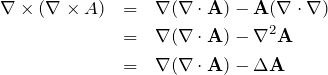
ここで、ラプラス演算子