双極モーメントについて学びましょう。2つのタイプがあります。電荷が作る電気双極子モーメントと磁場がつくる磁気双極子モーメントです。ここでは、電荷がつくるスカラーポテンシャルに注目して双極モーメントの基礎を学んでいく。四重極モーメントは別に扱う。
1. 双極モーメント
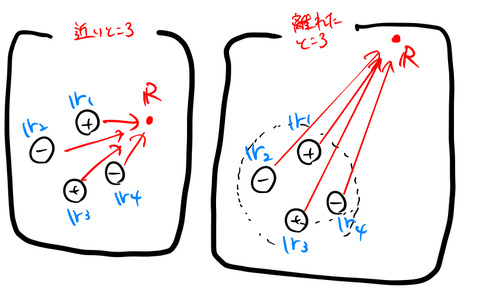
これは近似で、適用できる場面というものがある。適用できるのは、電荷がある系が考えている場より遠く離れている場合である。
絵を見て欲しい。考えている場 ![]() に比べて電荷が存在する系が離れている。この場合において、双極モーメントを考えることができる。
に比べて電荷が存在する系が離れている。この場合において、双極モーメントを考えることができる。
求めたいポテンシャルの場所が、電荷(磁場)が存在する系から十分離れている場合に、双極モーメントの扱いが大事になる。
左図の ![]() の近い領域だと以下の計算で出てくる展開が行えないので注意する。
の近い領域だと以下の計算で出てくる展開が行えないので注意する。
1.1 問題設定
問題設定は以下の通りである。
- 電荷のある系は考えている場
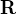 より離れている
より離れている - 座標の原点は電荷のある系(右図の点線の中)にとる
- それぞれの電荷の位置を
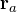 とする
とする - それぞれの電荷の電荷量を
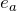 とする
とする
図の場合は電荷は ![]() から
から ![]() まである。
まである。
1.2 導出
まず、![]() にある1個の電荷が
にある1個の電荷が ![]() 作るスカラーポテンシャル
作るスカラーポテンシャル ![]() は、
は、
![]()
![]()
![]()
この展開はテイラー展開と同じである。関数 ![]() の
の ![]() に対応する部分がベクトルになっているため、
に対応する部分がベクトルになっているため、![]() となっている。ベクトルであることをわかりやすくすると、
となっている。ベクトルであることをわかりやすくすると、
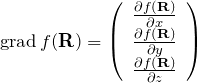
となる(![]() のとき)。
のとき)。
ポテンシャルを展開しよう。原点から ![]() までの距離
までの距離 ![]() とする。
とする。
![Rendered by QuickLaTeX.com \begin{eqnarray*}\varphi &=&\sum_a \frac{e_a}{|{\bf R} - {\bf r_a}|}\\&\sim&\sum_a \left[ \frac{e_a}{|{\bf R}|} - {\bf r}_a \cdot {\rm grad}\, \frac{1}{|{\bf R}|}\right]\\&=&\frac{\sum_a e_a}{R} - \left( \sum_a e_a {\bf r}_a \right)\cdot {\rm grad}\, \frac{1}{R} \\&=&\frac{\sum_a e_a}{R} - {\bf d}\cdot{\rm grad}\, \frac{1}{R}\quad \cdots (*) \\&&\quad \left({\bf d}\equiv \sum_a e_a {\bf r}_a \right)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-97dd0319a20b87a30e0723867caff45f_l3.png)
![]() は和
は和 ![]() に関係ないので、
に関係ないので、![]() の外に出しておく。また、最後の行で定義した
の外に出しておく。また、最後の行で定義した ![]() が双極モーメントと呼ばれるものである。ちょうど通常のモーメント
が双極モーメントと呼ばれるものである。ちょうど通常のモーメント
と似たような形になっている。
1.3 全電荷がゼロの場合
全電荷がゼロ、
![]()
![]()
となる。ここで、ベクトル ![]() を計算する。まず
を計算する。まず![]() 成分について計算する。
成分について計算する。![]() であることを思い出すと、
であることを思い出すと、
![Rendered by QuickLaTeX.com \begin{eqnarray*}\frac{\partial}{\partial x} \left[ \frac{1}{\sqrt{x^2+y^2+z^2}} \right]&=&\frac{\partial}{\partial x} \left[ \left(x^2+y^2+z^2\right)^{-\frac{1}{2}} \right]\\ \\&=&-\frac{1}{2}\, 2x \, \left(x^2+y^2+z^2\right)^{-\frac{3}{2}} \\ \\&=&\frac{-x}{\left(\sqrt{x^2+y^2+z^2}\right)^3 } \\ \\&=&\frac{-x}{R^3} \quad( \because \sqrt{x^2+y^2+z^2}=R )\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-146ee574f4381493263d1f2adbd2d760_l3.png)
となる。![]() 座標と
座標と ![]() 座標も同様に計算できる。
座標も同様に計算できる。
![]()
よって、
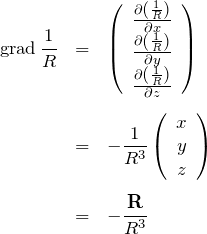
したがって全電荷が0の場合の遠く離れた場所のポテンシャルが計算できる。
![]()
1.4 電場 E の強さ
電場を求めるためにはスカラーポテンシャルの勾配をとればよい。全電荷がゼロのとき、
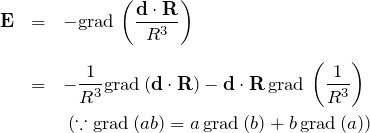
となる。最終的な結果は以下の通り。
![]()
2. まとめ
双極モーメントの導出をおこなってきた。![]() の計算はすこしややこしいかもしれないが、慣れれば簡単である。磁気双極モーメントについても同様の計算ができる。結局、遠く離れた場所に作るベクトルポテンシャルを展開していけばよい。
の計算はすこしややこしいかもしれないが、慣れれば簡単である。磁気双極モーメントについても同様の計算ができる。結局、遠く離れた場所に作るベクトルポテンシャルを展開していけばよい。
ここでは四重極モーメントについては触れていない。しかし、ポテンシャルの展開を2次の項までとることで容易に計算できるとわかるだろう。