電磁気学でよく習う ![]() は高校を卒業したての大学生の頭を困惑させる(rotation)。ここでは計算式など一切使わず、何を求めているのかイメージを掴んでもらいたい。
は高校を卒業したての大学生の頭を困惑させる(rotation)。ここでは計算式など一切使わず、何を求めているのかイメージを掴んでもらいたい。
1. 回転(rot)の意味
ベクトル解析の勾配、発散、回転は初学者キラーの三銃士である。ここで扱う回転を攻略するには、流れに「風車」をぶっさせばよい。
1.1 風車をぶっさす
ベクトルの回転(rot)は流れ(ベクトル)に作用する。ベクトルの矢印の大きさはその場での流れの強さを表している。流れは風の流れでも良いし水の流れでも良い。ここでは、風の流れをイメージしてみる。
ベクトルの回転が 0 ではないとはどういうことか?風の流れをベクトル ![]() で表しておく。図のように立てた風車(かざぐるま)*1は、風の流れベクトル
で表しておく。図のように立てた風車(かざぐるま)*1は、風の流れベクトル ![]() によって回転するだろう。
によって回転するだろう。
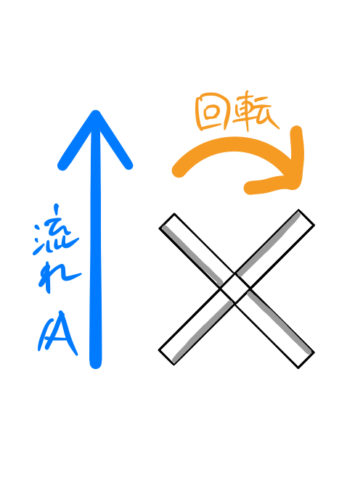
風車が回転する場合は、![]() である。つまり、流れをベクトルとして、ベクトル場に風車を立てて回転するかどうか調べるのが、
である。つまり、流れをベクトルとして、ベクトル場に風車を立てて回転するかどうか調べるのが、![]() の意味である。
の意味である。
さらに、風車が早く回転するほど流れが強いということも簡単にわかると思う。
1.2 風車の軸と回転(rot)の向き
いま、平面を考えて風車が回転するか見た。したがって風車の軸は勝手に決めてしまっていた。流れが ![]() の3次元であるなら、風車は3次元的に回転するはずである。
の3次元であるなら、風車は3次元的に回転するはずである。
これが ![]() がベクトル量である理由である。つまり、下のような3つの風車を用意して、ベクトルの回転をみる。
がベクトル量である理由である。つまり、下のような3つの風車を用意して、ベクトルの回転をみる。
 軸方向に軸を持った風車
軸方向に軸を持った風車 軸方向に軸を持った風車
軸方向に軸を持った風車 軸方向に軸を持った風車
軸方向に軸を持った風車
先ほどの例の風車の軸が ![]() 軸方向にあるとする。すると下図のようになる。
軸方向にあるとする。すると下図のようになる。
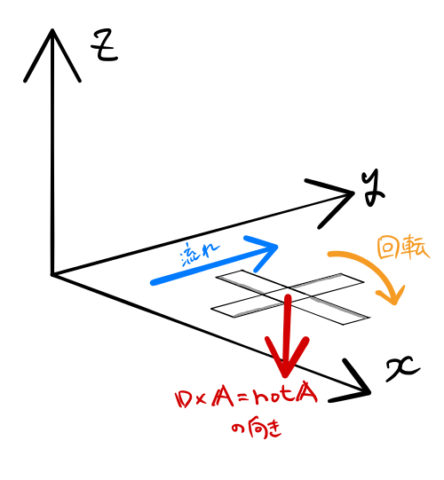
残るは ![]() が
が ![]() 軸方向のプラスの向きかマイナスの向きかである。しかしこれは、右ねじの回す向きと決められている。
軸方向のプラスの向きかマイナスの向きかである。しかしこれは、右ねじの回す向きと決められている。
今の場合、オレンジの「回転」方向にネジを締めるときに、ネジが進む向きに対応する(図の赤)。
ここまでをまとめると、「ベクトルの回転をとる」とは、風の流れによって風車が
- 3次元的にどの方向に回転するか
- どのくらいの速さで回転するか
を調べることである、というイメージである。
2. いろいろな場の例をみる
いろいろなベクトル場に風車を立ててみて、ベクトルが回転しているかみてみる。
2.1 ベクトルの回転が0でない例
いろいろなベクトル場を見てみる。まず、風車を立てて回転するか調べた時に、回転する場合 ![]() の例を紹介する。
の例を紹介する。
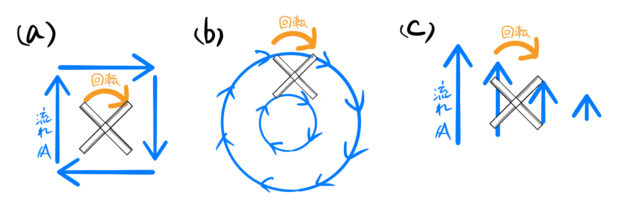
(a) 平面内で回転していることがわかる。それぞれの流れが時計回りに風車を回してることは簡単にわかる。この場合、![]() である。向きは画面の奥向きである。
である。向きは画面の奥向きである。
(b) 同じく平面内で回転している同心円上の場を考えた。わかりにくいかもしれないが、外側の円ほど風の流れは強い場合を描いている。注意点は、外側の円の流れと内側の円の流れが同じ場合は ![]() で回転しない(1.4で確認)。
で回転しない(1.4で確認)。
(c) 左のほうが流速が大きい場合。左の流れが右の流れに打ち勝つために、風車は回転する。したがって、![]() である。
である。
このように、明らかにベクトル場によって回転することがわかる例もある。
2.2 ベクトルの回転が0になる例
続いて、![]() になるベクトル場を見てみる。
になるベクトル場を見てみる。
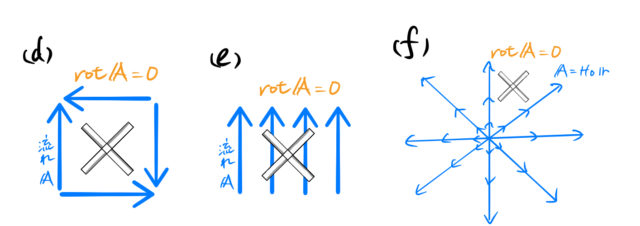
(d) 2.1の図(a) と似ているが、流れの向きが異なる。それぞれの4方向の流れが打ち消しあって、![]() になる。
になる。
(e) 均一に流れている場でも、同じく ![]() になる。2.1 の図(c) と異なり、左右の流れが相殺することによる無回転。
になる。2.1 の図(c) と異なり、左右の流れが相殺することによる無回転。
(f) 流れの源泉(中心)からの距離に比例する大きさのベクトル場 ![]() である。図の場合だと、流れによる回転がそれぞれ打ち消し合っている。(実際に計算すれば
である。図の場合だと、流れによる回転がそれぞれ打ち消し合っている。(実際に計算すれば ![]() は確認できるが、ここでは計算はしない。)
は確認できるが、ここでは計算はしない。)
補足として最後の、
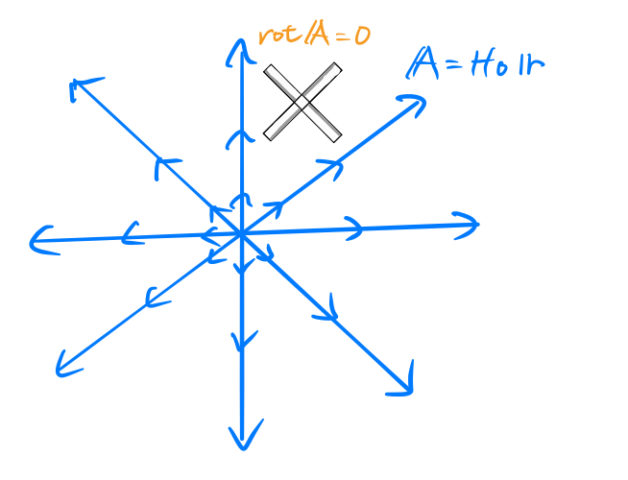
は膨張宇宙を表している。![]() はハッブルパラメータで、遠くにある天体ほど大きな速度で中心から離れていく様子を示している。*2
はハッブルパラメータで、遠くにある天体ほど大きな速度で中心から離れていく様子を示している。*2
3. まとめ
流れパターンだけまとめたものを締めに再度載せておく。
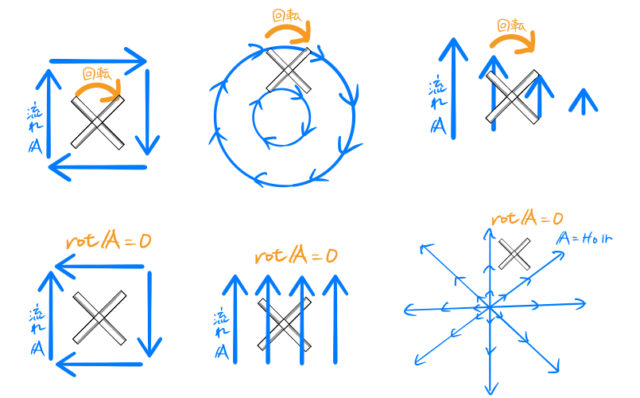
計算式はすっとばしてイメージだけを伝えてきた。誰かの参考になればいいのだが。超絶参考になったわかりやすいベクトル書籍は下のやつ。
*1
「かざぐるま」は小さくて軽いおもちゃのようなもの。「ふうしゃ」は発電用のもの。このような違いがあるらしい。「ふうしゃ」のほうが重くて回転しにくいイメージがあるので、この記事では風車を「かざぐるま」とした。
*2
この中心は、太陽としてもプロキシマ・ケンタウリとしても変わらず、宇宙は一様に膨張する。らしい。
本説明文作成の方へ:
ベクトル解析の勉強をしているものです。教科書として使用してる本が中々理解できず、ネットで理解を深めるため色々と探してました。本説明文が大変分かりやすく、コピーさせて頂くことは出来ないでしょうか。よろしく願います。
※私、好きで数学・物理に触れる、現在は隠居の身です。
ありがとうございます。
プリンター印刷という意味でしたら可能です。本文のコピーも私的利用の範囲で可能です。
配布などはお控えください。