強制振動とは、ブランコに乗っている人を後ろから押してやるみたいに、振動数![]() で自由振動している系を外場
で自由振動している系を外場 ![]() によって強制的に振動させる運動のことである。もともとの
によって強制的に振動させる運動のことである。もともとの ![]() に近い振動数で外場
に近い振動数で外場 ![]() を与えたときには「うなり」が発生する。以下の 442Hz と 438Hz の「うなり」はWikipediaより引用した(音が出ます)。
を与えたときには「うなり」が発生する。以下の 442Hz と 438Hz の「うなり」はWikipediaより引用した(音が出ます)。
摩擦のない場合の強制振動 の運動方程式は下のようになる。ここでは、「うなり」を運動方程式の一般解から見ていくことでゆるキャラ*1 のように親しめるようになる。
![]()
1. うなり とは?
「うなり」は振動数がある程度近い2つの波が重なり合う時に、波(振幅)の強弱ができる。2つの音波の場合は、「ウォーンウォーン」といったように聞こえる。以下の音源は Wikipedia から引用した。438Hzと442Hzの音源によるうなりである(音が出ます)。
高校物理で習う、うなりの振動数 ![]() は 2つの波の振動数
は 2つの波の振動数 ![]() に対して、
に対して、
![]()
となる。
2. うなりを強制振動から考える
「うなり」を強制振動の運動方程式から見る。もともとの自由振動(単振動)の振動数を ![]() とする。外部から時間の周期関数である外場
とする。外部から時間の周期関数である外場
![]()
を加える。ここで扱う強制振動は以下のような物理現象と関わりがある。
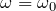 :共鳴(一般解)
:共鳴(一般解)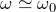 :うなり
:うなり
![]() を微小量として振動数
を微小量として振動数 ![]() をもった周期的な外場を考える。わかりやすく上の音波のうなりの例で表すと
をもった周期的な外場を考える。わかりやすく上の音波のうなりの例で表すと
になる。
強制振動の運動方程式と一般解
一般的な強制振動の運動方程式は、
![]()
である。この非同次線形微分方程式の一般解は、同次線形微分方程式
![]()
で表された自由振動の一般解 ![]() と特殊解
と特殊解 ![]() で表すことができる。したがって、以下のようになる。
で表すことができる。したがって、以下のようになる。
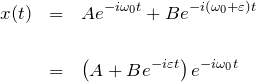
![]() は位相因子を含むため、複素数で表される。ここで、
は位相因子を含むため、複素数で表される。ここで、![]() が微小量であるため、
が微小量であるため、![]() の周期
の周期 ![]() の間に、
の間に、![]() の部分はほとんど変化しない(後の図の赤波に対応)。
の部分はほとんど変化しない(後の図の赤波に対応)。
合成波の「振幅」
ほとんど変化しない部分の振幅を ![]() として
として ![]() を見る。複素数
を見る。複素数 ![]() をそれぞれ
をそれぞれ ![]() と表す。
と表す。
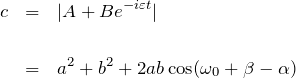
![]() より、
より、
![]()
すなわち、2つの波を合成した波の「振幅」 ![]() は
は ![]() の間を振動数
の間を振動数 ![]() で周期的に振動する。
で周期的に振動する。
442 Hz と 438 Hz のうなり
再度、442 Hz と 438 Hz の例をみる。
442 Hz と 438 Hz のそれぞれの振幅が同じ(![]() )とき、
)とき、
![]()
である。2つの波の山と谷が重なれば音は合成波の振幅は0で音は聞こえない。また、2つの波の山と山が重なれば音は大きく聞こえる。
具体的に、![]() [Hz]の波は1秒間に442回振動する。
[Hz]の波は1秒間に442回振動する。![]() [Hz] も同様である。この2つの波は時間が経過するごとに少しずつ山の位置がずれていく。
[Hz] も同様である。この2つの波は時間が経過するごとに少しずつ山の位置がずれていく。
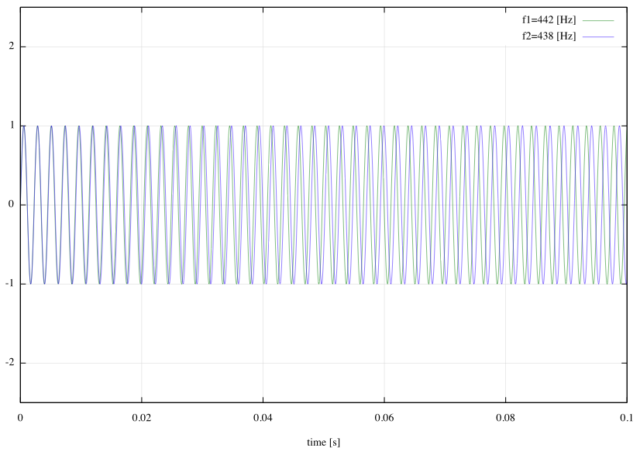
この2つの波の重ね合わせは以下のようになる。振動数 ![]() の波は赤色で描いた。時間スケールが上の図と異なることに注意する。
の波は赤色で描いた。時間スケールが上の図と異なることに注意する。
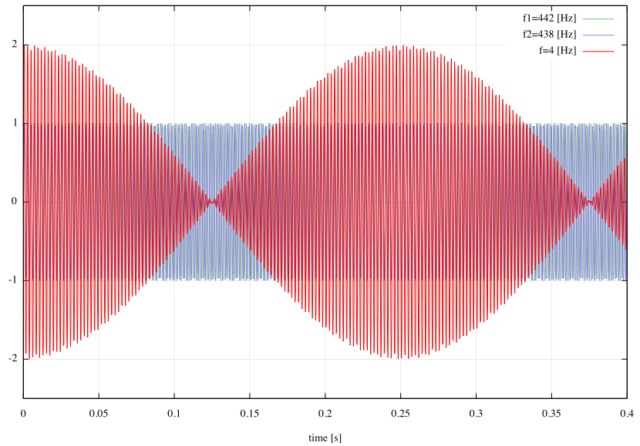
![]() の波は、1秒ごとに4回振動する。つまり、0.25秒ごとに1回振動する。上の図からそのことがわかるし、音源を聴き直してみればそんな気がする。我々が「ウォーンウォーン」と聞こえているうなりはこの赤い波である。
の波は、1秒ごとに4回振動する。つまり、0.25秒ごとに1回振動する。上の図からそのことがわかるし、音源を聴き直してみればそんな気がする。我々が「ウォーンウォーン」と聞こえているうなりはこの赤い波である。
赤い波の振幅は ![]() である。また赤い波の式は
である。また赤い波の式は ![]() の振動(
の振動(![]() )を
)を ![]() (例では
(例では ![]() )で変調した形になっている。つまり下の形になっている。
)で変調した形になっている。つまり下の形になっている。
![]()
3. まとめ
「うなり」を強制振動から見てきた。自由振動の振動数に近い振動数をもつ外場によって「うなり」がおこっていることが確認できたと思う。
この「うなり」はバイオリンやギターなどの弦楽器のチューニングにも使われる。よくある方法として、音叉などを使って振動数 ![]() が 440Hz のA(ラ)の音を出し、チューニングする楽器の音の振動数
が 440Hz のA(ラ)の音を出し、チューニングする楽器の音の振動数 ![]() を変えていき、「うなり」が消える場所を探す。「うなり」が消えているところでは
を変えていき、「うなり」が消える場所を探す。「うなり」が消えているところでは ![]() は
は ![]() に等しく、これでチューニングが完了する。実際は、これ以外にもいろいろな方法がある。
に等しく、これでチューニングが完了する。実際は、これ以外にもいろいろな方法がある。