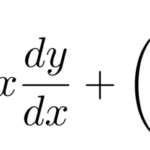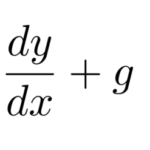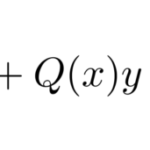ここでの目的は、線形型の微分方程式
![]()
の解き方を習得し、例題を解けるようになることである。このタイプを解くには以下のコツだけ覚えていれば、後に示すような難しい一般解は不要になる。
- 「何か」を両辺にかけて、
![Rendered by QuickLaTeX.com \frac{d}{dx}\left[\rule[-2mm]{10mm}{5mm}\right]](https://batapara.com/wp-content/ql-cache/quicklatex.com-00c8f26170792f31831dd4e8ba7a366a_l3.png) の形を作る
の形を作る - その何かとは以下のものである。
![]()
例題はこちら。
以下の微分方程式を解け。
目次
1. 線形型微分方程式と例題から理解する解法の指針
微分方程式の一般解がどのように導出されたか、 その考え方・着想を辿っていきたい。ここで扱う線形型は冒頭で示した、
![]()
のタイプである。
一般解を見せておく
あとで導出される一般解を先に示しておこう。
![]()
これは魔界である。こんなものは覚えてはならない。どうせ間違って覚えてしまうのだ。
そういうわけで、ここでは「一般解を導く方法を覚える」という方針で説明する。
例題から学ぶ
次章では一般的な式を解いていく。ここではその土台を作るため、例題(1)を解く考え方を追っていこう。もちろん上の一般解の式は使わない、絶対に。
与えられた微分方程式は
![]()
であった。これは変数分離型で解けるが、ここで学ぶ手法でも解ける。
まず、![]() の係数は1にすることで線形型であることを確認する。
の係数は1にすることで線形型であることを確認する。
![]()
確かに線形型である。
微分方程式を解くために次に一番重要なことがある。左辺を
![]()
の形にすることを目指すことである。つまり、何かの合成関数を微分した結果が ![]() になっていると考える。上の形が実際にできれば、
になっていると考える。上の形が実際にできれば、
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\frac{d}{dx} \left[\rule[-2mm]{10mm}{5mm}\right]=0\\\\ \Leftrightarrow \quad &&\rule[-2mm]{10mm}{5mm}=C \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-3fe280bae023c2394711c59548c5630d_l3.png)
と積分してやれば良い。
今の問題は、どのように黒い部分を作るかということである。 おそらく両辺に何かかけておけば、合成関数の微分の形にできそうである。
ここでの答えは ![]() を両辺にかければ良い。 実際に左辺は
を両辺にかければ良い。 実際に左辺は
![]()
となり、合成関数の微分で表された。 したがって、微分方程式は以下のように解ける。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\frac{d}{dx}\left[\textcolor{red}{\frac{1}{x}y}\right]=0\\\\ \Leftrightarrow \quad&&\frac{1}{x}y=C\\\\ \Leftrightarrow \quad&&y=Cx\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-21c3068c3825bd41181518e75098ac9c_l3.png)
両辺に何をかけるべきかは勘ではなかなか難しい。ここで「両辺にかけるべきもの」は
![]()
だと計算できる。この左辺の謎の「指数関数with積分肩乗せ」については、次の章の一般的な形のところで説明していく。
後にわかるように、一般に両辺にかけるべきものは
![]()
である。
2. 一般的な形から一般解を導出
以下、一般的な解き方になる。 上で見た具体例を一般化していく。
線形型を解くための指針
![]()
を
![]()
の形になんとかできれば、両辺を積分することで
![]()
と解けるはずである。したがって、今目指すべきは、 真っ黒い部分の形に変形できるような操作をおこなうことである。
真っ黒い部分をつくる(合成関数の微分の形に持っていく。)
左辺を工夫する
黒い部分を作るため、もとの微分方程式の両辺に ![]() をかけてみる。
をかけてみる。
![]()
左辺を合成関数の微分の形として置いてみる。
![]()
この右辺の微分を実行すると
![]()
となる。これを ![]() に等しいとして
に等しいとして
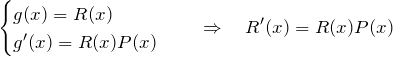
この式、わかるだろうか。変数分離型になっているということを。 ![]() と略記すると、
と略記すると、
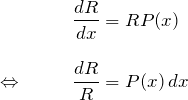
となる。したがって、これは変数分離型で解ける。
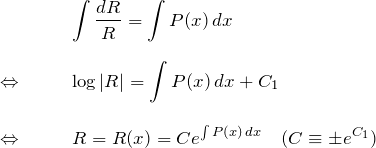
ということは、この ![]() をもとの微分方程式の両辺にかけておけばよいということがわかる。実際にかけてみよう。両辺にかけるため、定数項は無視して良い(
をもとの微分方程式の両辺にかけておけばよいということがわかる。実際にかけてみよう。両辺にかけるため、定数項は無視して良い(![]() )。
)。
![Rendered by QuickLaTeX.com \begin{eqnarray*} e^{\int P(x) \, dx}y'+ e^{\int P(x) \, dx}P(x)y&=& e^{\int P(x) \, dx} Q(x)\\\\ \frac{d}{dx}\left[\textcolor{red}{e^{\int P(x) \, dx} y}\right]&=&e^{\int P(x) \, dx}Q(x) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-cd927d6509cf7a2e71739f8877209e43_l3.png)
1行目は余計ややこしく見えるが、2行目では左辺が合成関数の微分にまとめられるためスッキリする。両辺を積分してやれば、 一般解を得る。
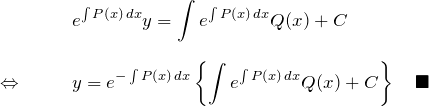
これが初めに示した一般解である。そして覚えてはならない式である。
両辺にかけるべきもの
上の計算でわかったことは、両辺にかけるべきものが ![]() であるということだ。 つまり、微分方程式の両辺に
であるということだ。 つまり、微分方程式の両辺に
![]()
をかければ良い。
その結果、合成関数の微分の形がつくれることは上で示した通りである。
この2つのポイントだけ覚えれば良い
結果をまとめておこう。結局このページで覚えることは以下の2点だけである。
![]()
の線形微分方程式を解くためには以下のことだけ押さえておけば良い。
- 「何か」を両辺にかけて、
![Rendered by QuickLaTeX.com \frac{d}{dx}\left[\rule[-2mm]{10mm}{5mm}\right]](https://batapara.com/wp-content/ql-cache/quicklatex.com-00c8f26170792f31831dd4e8ba7a366a_l3.png) の形を作る
の形を作る - その何かとは以下のものである。
![]()
あとは例題を解いて、その仕組みを理解していくのが良い。
3. 例題の解答
以下、![]() などは定数である。
基本的に、両辺に「何か」をかけて合成関数の微分を作るという方針で解く。
などは定数である。
基本的に、両辺に「何か」をかけて合成関数の微分を作るという方針で解く。
例題(1)の解答
【解答】 線形微分型に見えるように変形:
![]()
両辺にかけるもの:
![]()
両辺に ![]() をかける:
をかける:
![]()
合成関数の微分の形をつくって積分:
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\frac{d}{dx}\left[\frac{1}{x}y\right]=0\\\\ \Leftrightarrow\quad&&\frac{1}{x}y=C\\\\ \Leftrightarrow\quad&&y=Cx\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b893c91a368ac60c43eff6bce2678df5_l3.png)
例題(2)の解答
微分方程式を変形:
![]()
両辺にかけるもの:
![]()
両辺に ![]() をかける:
をかける:
![]()
合成関数の微分の形をつくって積分:
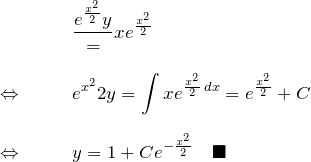
例題(3)の解答
微分方程式:
![]()
両辺にかけるもの:
![]()
両辺に ![]() をかける:
をかける:
![]()
合成関数の微分の形をつくって積分:
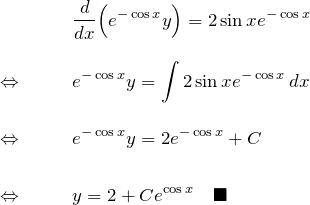
4. まとめ
ここのポイントは公式を覚えないということである。 ただし、「何かをかければうまい変形」ができるということさえ理解しておいてほしい。
一般解の形を覚えるために使っていた脳の容量は、別の物事を覚えるために空けておくのが良かろう。